Уравнения амплитудной и фазовой частотных характеристик

Видео:Понятия: амплитудно-частотная, фазо-частотная характеристики - часть 10Скачать

Амплитудные и фазовые частотные характеристики

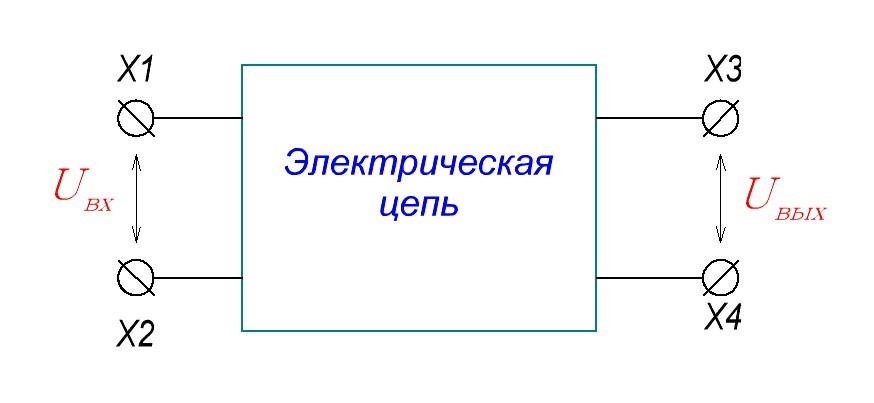
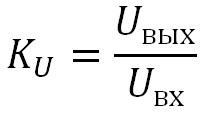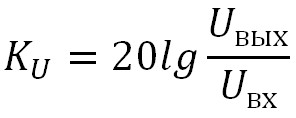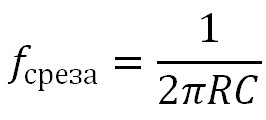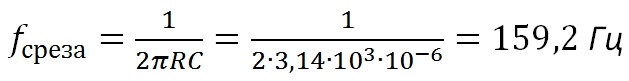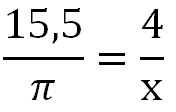Известно, что динамические процессы могут быть представлены частотными характеристиками (ЧХ) путем разложения функции в ряд Фурье.

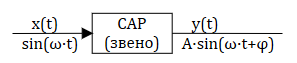
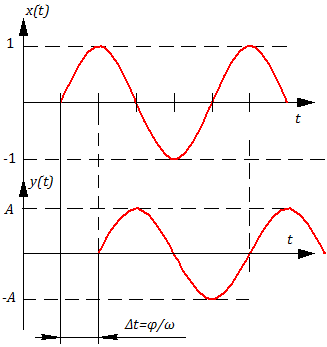
Предположим, имеется некоторый объект и требуется определить его ЧХ. При экспериментальном снятии ЧХ на вход объекта подается синусоидальный сигнал с амплитудой А_вх = 1 и некоторой частотой w, т.е.

Тогда после прохождения переходных процессов на выходе мы будем также иметь синусоидальный сигнал той же частоты w, но другой амплитуды А_вых и фазы j:

При разных значениях w величины А_вых и j, как правило, также будут различными. Эта зависимость амплитуды и фазы от частоты называется частотной характеристикой. Виды ЧХ:

АФХ – амплитудно-фазовая характеристика — зависимость амплитуды и фазы выходного сигнала от частоты входного (изображается на комплексной плоскости);

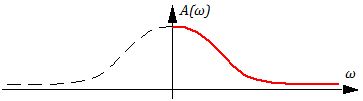
АЧХ – амплитудно-частотная характеристика — зависимость амплитуды выходного сигнала от частоты входного: А(w);

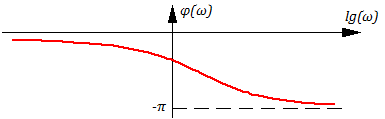
ФЧХ – фазо-частотная характеристика — зависимость фазы выходного сигнала от частоты входного: j(w) ;

ЛАХ, ЛАЧХ — логарифмические АЧХ, т.е. построенные в логарифмических координатах.

На комплексной плоскости входная величина x = А_вх . sin(wt) для каждого момента времени t_i определяется вектором х на комплексной плоскости. Этот вектор имеет длину, равную А_вх, и отложен под углом wt_i к действительной оси (Re — действительная ось, Im — мнимая ось).

Тогда величину х можно записать в комплексной форме

(t) = А_вх(cos(wt) + j . sin(wt)),

где j = — мнимая единица.

Или, если использовать формулу Эйлера e j a = cosa + j . sina, то можно записать

(t) = А_вх . e j w t .

Выходной сигнал y(t) можно аналогично представить как вектор

(t) = А_вых . e j ( w t + j ) .

Рассмотрим связь передаточной функции и частотной характеристики.

Определим производные по Лапласу:

Определим производные ЧХ:

у’(t) = jw А_выхе j ( w t + j ) = jw у,

у”(t) = (jw) 2 А_выхе j ( w t + j ) = (jw) 2 у и т.д.

Отсюда видно соответствие s = jw.

Вывод: частотные характеристики могут быть построены по передаточным функциям путем замены s = jw.

Для построения АЧХ и ФЧХ используются формулы

, ,

где Re(w) и Im(w) – соответственно вещественная и мнимая части выражения для АФХ.

Формулы получения АФХ по АЧХ и ФЧХ:

Re(w) = A(w) . cos j(w), Im(w) = A(w) . sin j(w).

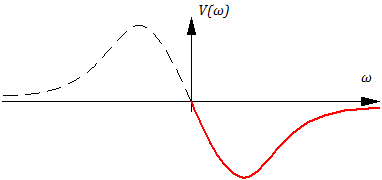
График АЧХ всегда расположен в одной четверти, т.к. частота w > 0 и амплитуда А > 0. График ФЧХ может располагаться в двух четвертях, т.е. фаза j может быть как положительной, так и отрицательной. График АФХ может проходить по всем четвертям.

При графическом построении АЧХ по известной АФХ на кривой АФХ выделяются несколько ключевых точек, соответствующих определенным частотам. Далее измеряются расстояния от начала координат до каждой точки и на графике АЧХ откладываются: по вертикали – измеренные расстояния, по горизонтали – частоты. Построение АФХ производится аналогично, но измеряются не расстояния, а углы в градусах или радианах.

Для графического построения АФХ необходимо знать вид АЧХ и ФЧХ. При этом на АЧХ и ФЧХ выделяются несколько точек, соответствующих некоторым частотам. Для каждой частоты по АЧХ определяется амплитуда А, а по ФЧХ – фаза j. Каждой частоте соответствует точка на АФХ, расстояние до которой от начала координат равно А, а угол относительно положительной полуоси Re равен j. Отмеченные точки соединяются кривой.

Видео:Логарифмическая амплитудная характеристика САУ: построение ЛАХ для конкретной системыСкачать

3. Частотные характеристики систем автоматического управления (АФЧХ, ЛАХ, ФЧХ) ч. 3.1

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В этом разделе мы будем изучать частотные характеристики. Тема сегодняшней статьи:
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ

Будет интересно, познавательно и жестко.

Видео:Амплитудно-частотная и фазо-частотная характеристики(АЧХ и ФЧХ) последовательной RLC цепи. ЗадачаСкачать

3.1. Амплитудно-фазовая частотная характеристика: годограф АФЧХ, ЛАХ, ФЧХ

Определение: Частотными характеристиками называются формулы и графики, характеризующие реакцию звена (системы) на единичное синусоидальное воздействие в установившемся режиме, т.е. в режиме вынужденных гармонических колебаний звена (системы).

Формула синусоидального воздействия может быть записана как:

— сдвиг фазы (нередко называют — фаза);
— амплитуда;
т.е. амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия x(t).

Используем показательную форму записи функции единичного гармонического воздействия и отклика на это воздействие (рис. 3.1.1):

Определим связь между передаточной функцией и гармоничным воздействием, пользуясь показательной формой.
Рассмотрим звено уравнение динамики которого имеет следующий вид:

В показательной форме:

Запишем в показательной форме используя соотношения 3.1.1:

Подставим эти соотношения в (3.1.1) получим:

Поскольку (амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия), то можно записать:

если вспомнить, что в преобразования Лапласа , то:

Получаем выражение для передаточной функции

— Амплитудно-фазовая частотная характеристика (АФЧХ)
Иногда называют частотной передаточной функцией.
Модуль АФЧХ= тождественно равен амплитуде выходного сигнала:

Сдвиг фазы выходного сигнала:

Обычно АФЧХ изображается на комплексной плоскости. Формулы (3.1.6) и (3.1.7) позволяют изобразить в полярных координатах
Так же можно изображать в традиционных декартовых координатах:

Если использовать для представления W(s) форму W(s)=K·N(s)/L(s), где L(s)- полиномы по степеням s, (причем свободные члены равны 1), а К – общий коэффициент усиления звена (системы), то

Сдвиг фазы можно определить по виду многочленов и (см. формулу (3.1.9)) т.е. как разность фаз (аргументов) числителя и знаменателя:

Постоим АФЧХ для «абстрактного» звена (системы) с передаточной функцией:

Подставляя в формулу различные значения , получаем набор векторов, на комплексной плоскости

Рассмотрим действительную и мнимую части полученных векторов Из рисунка 3.1.3 видно, что:

Амплитуда и сдвиг фазы рассчитываются для векторов, соответствующих положительным частотам и лежащих в 4 квадранте по формулам:

В общем случае для любых углов сдвига необходимо учитывать переход между квадрантами на плоскости. Тогда формула принимает вид:

где:
j = 0, 2, 3, 4. если вектор в I и IV квадрант;
j = 1, 3, 4, 4. если вектор в II и III квадранте.

Во всех технических системах отклик системы, как правило, отстает от входного воздействия, то есть сдвиг фазы всегда отрицательный. Исходя из формулы 3.1.10, степень полинома L(s) выше, чем полинома N(s). Поскольку обычно степень полинома L(s) выше, чем полинома N(s), то с увеличением частоты на входе в звено (в систему) сдвиг фазы обычно отрицателен, т.е. сигнал на выходе звена еще больше отстает по фазе от входного сигнала при увеличении частоты.
В предельном случае, если частота растет до бесконечности, мы можем вообще не получить выходного воздействия. Обычно при ω→ ∞ величина амплитуды на выходе звена стремится к 0, то есть lim A(ω→∞) = 0.

при замене на имеет зеркальное изображение.

Анализируя годографы АФЧХ при > 0 (сплошная линия на рисунке 3.1.3) и при Рисунок 3.1.4 – «Зеркальная» симметрия относительно оси ординат.

Кроме анализа свойств звена (системы) по годографу АФЧХ, широкое распространение получили анализ логарифмической амплитудной характеристики (ЛАХ) и фазочастотной характеристики (ФЧХ).

ЛАХ определяется как Lm(ω)=20lgA(ω).

Поскольку зачастую удобнее использовать десятичные логарифмы (lg), чем натуральные(ln), в теории управления (также и в акустике) значительно чаще используется специальная единица – децибел (1/10 часть Бела):
+1Бел – единица, характеризующая увеличение в 10 раз.
+1дБ (децибел) – соответствует увеличению в раз.

В формуле Lm(ω)=20lgA(ω) величина Lm(ω) измеряется также в децибелах. Происхождение множителя 20 таково: A(ω) – амплитуда, линейная величина, а мощность — квадратичная величина (например, напряжение в сети измеряется в Вольтах, а мощность () пропорциональна квадрату напряжения, поэтому в формуле для Lm(ω) стоит множитель 20 (чтобы привести ЛАХ (Lm(ω)) к традиционной мощностной характеристике).

Если больше на 20 дБ, то это означает, амплитуда больше амплитуды в 10 раз,

Окончательно: Lm(ω)=20lg│W(iω)│= 20lgA(ω)

Из этого следует, что +1 децибел (+1 дБ) соответствует увеличению амплитуды в раз (очень малая величина); -1 дБ – уменьшение амплитуды в раз.

Графики A(ω) и φ(ω) имеют вид:

Учитывая, что “ω” обычно изменяется на порядки и значение A(ω) – также на порядки, график Lm(ω) строится, фактически, в логарифмических координатах, т.е. Lm(ω) =Lm(lg(ω)), например:

Наклон (– 40 дБ/дек) соответствует уменьшению амплитуды в 100 раз при увеличении частоты в 10 раз.

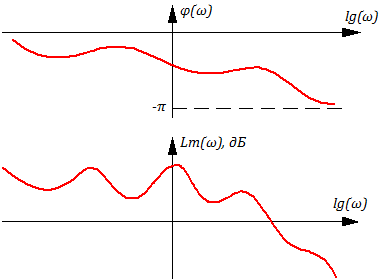
Рассмотренные характеристики Lm(ω), то есть ЛАХ и ФЧХ имеют широкое распространение при анализе динамических свойств звена (системы), например, при анализе устойчивости САР (см. раздел “Устойчивость систем автоматического управления”).

Рисунок 3.1.10 – пример ЛАХ и ФЧХ для сложной системы

Пример 1

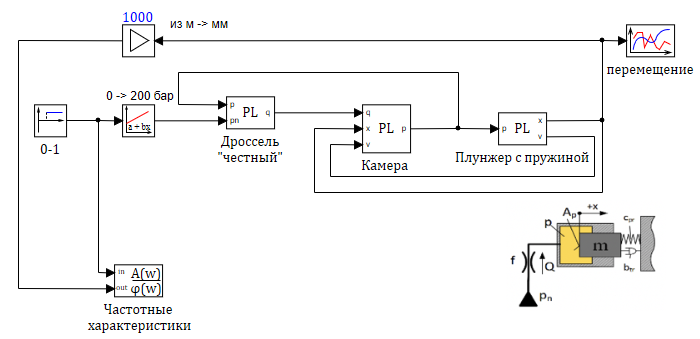
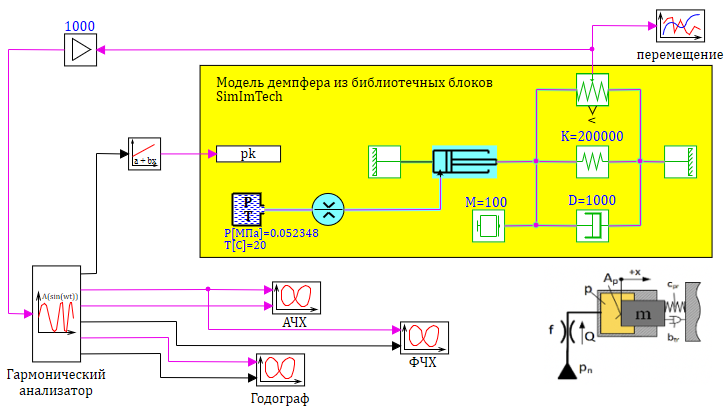
В качестве примера построим АФЧХ для демпфера, модель которого разобрана в этой статье. . Добавим на схему блок «Построение частотных характеристик», в качестве входа возьмем возмущающее воздействие, в качестве выхода — положение положение груза. Для наглядности иллюстрации примем в качестве выхода положение в миллиметрах (х1000), поскольку модель у нас размерная и результат получается в метрах уже достаточно маленьким примерно 0.004 метра. см. рис. 3.11

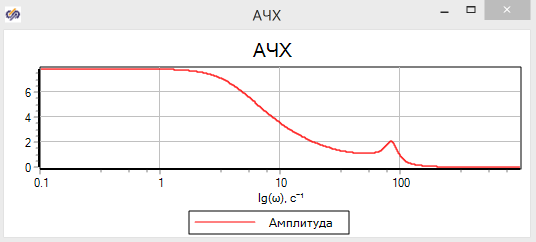
Параметры блока «Построение частотных характеристик» приведены на рисунке 3.1.12, для иллюстрации зависимости АЧХ и ЛАХ. Результат работы блока — график с выбранными параметрами — изображен на рисунке 3.1.13:

Анализ графика в линейном масштабе по ω чаще всего не очень удобен, поскольку весь график собирается в узкой области, а дальше график абсолютной амплитуды практически сливается с 0. Если мы хотим исследовать частоты хотя бы до 1000 Гц, мы увидим практически вертикальные и горизонтальные прямые. Изменения масштаба шкалы АЧХ и ω на логарифмический дает возможность лучше исследовать частотные характеристики (см. рис. 3.1.14).

На рисунке 3.1.14 представлены частотные характеристики демпфера в логарифмическом масштабе и иллюстрация соотношения между абсолютной величиной амплитуды АФЧХ и ЛАХ в децибелах.

Пример 2

Постоим частотные характеристики для чуть более сложной модели, а именно — для гидравлического демпфера, рассмотренного в предыдущей лекции.

Для начала посмотрим на модель в виде блоков.

Модель, подготовленная для анализа, представлена на рисунке 3.1.15. В отличие от исходной модели, описанной ранее, входное воздействие задается блоком «ступенька» с скачком с 0 до 1 на 10 секунде расчёта. В блоке «линейная функция» происходит пересчет сигнала «ступенька»:
0 — соответствует 200 бар в камере (конечное состояние в предыдущем примере)
1 — соответствует 400 бар в камере.
Это сделано для того, чтобы можно было подавать синусоидальный сигнал и не получать отрицательное давление в камере плунжера. Также для наглядности графика мы усиливаем выходное перемещение, переводя его из метров в миллиметры.

Частотные характеристики, получаемые в конце расчёта, приведены на рисунке 3.1.16. Видно что характеристики отличаются от простого пружинного демпфера (сравните с 3.1.14)

Блок «Построение частотных характеристик» осуществляет расчет характеристик для линеаризованной модели в окрестности заданной точки. Это означает, что частотные характеристики системы в разные моменты времени могут отличаться для нелинейных моделей. Например, в нашем случае характеристики в начале расчёта будут отличаться от характеристик, полученных в конце расчёта.

Для подробных и нелинейных моделей, блок «Построение частотных характеристик» может не работать из за наличия разрывов и нелинейностей в модели. Как например, для «точной» модели демпфера, которую мы проверяли в предыдущей статье. В этом случае возможно построить частотные характеристики непосредственно моделированием, путем подачи синусоидального сигнала с разной частотой и измерения отклика. В SimInTech для этого используется блок «Гармонический анализатор», который подключается ко входу модели и генерирует синусоидальное воздействие. В этот же блок направляется отклик системы, и производится вычисление необходимых параметров для построения различных характеристик системы, которые можно вывести на графики с помощью блока «фазовый портрет».

Модель гидравлического демпфера, собранного из библиотечных блоков SimInTech, представлена на рисунке 3.1.7

Расчеты с моделью показывают, что при сохранении общего вида графиков значения, полученные для «подробной модели», отличаются от линеаризованной модели (см. рис. 3.18 — 3.19)

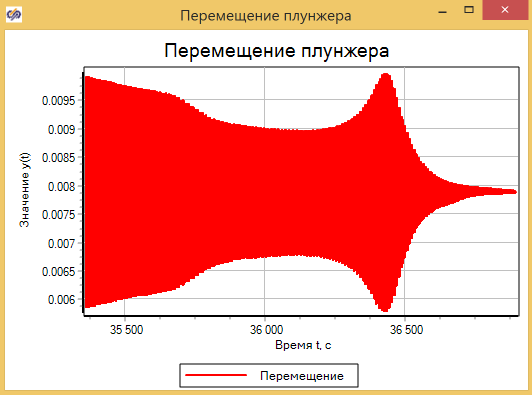
Использование прямого моделирования для получения характеристик является более надежным способом и работает не только с линейными моделями, но также может быть применимо для построения характеристик некоторых реальных объектов, если их можно подключить к среде моделирования и воздействовать в реальном режиме времени. Однако затраты на вычисления значительно будут больше. Например, для получения характеристик демпфера пришлось выполнить процесс в 40 000 секунд модельного времени, на обычном компьютере это заняло порядка 35 минут. График процесса перемещения плунжера в процессе вычисления характеристик приведен на рисунке 3.1.20.

Блок «Гармонический анализатор» имеет выходы:
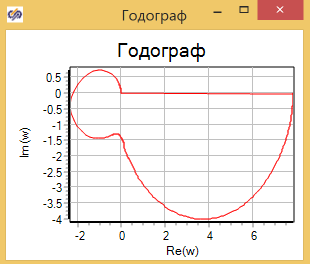
Re(w*t) – текущее значение действительной части амплитудно-фазовой частотной характеристики исследуемой системы;
Im(w*t) – текущее значение мнимой части амплитудно-фазовой частотной характеристики.
Это позволяет построить годограф исследуемой системы с помощью фазового портрета. (см. рис. 3.1.21)

Модели, использованные для иллюстрации в лекции можно взять здесь…

Видео:c03 8, Динамические звенья 1: амплитудно фазовая частотная характеристикаСкачать

Что такое АЧХ и ФЧХ

Видео:9) ТАУ для чайников. Части 3.7 и 3.8: Частотные характеристики.Скачать

Амплитудно-частотная характеристика

Аббревиатура АЧХ расшифровывается как амплитудно-частотная характеристика. На английском этот термин звучит как «frequency response», что в дословном переводе означает «частотный отклик». Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов. АЧХ устройства определяется по зависимости коэффициента передачи (или коэффициента усиления) от частоты.

Коэффициент передачи

Что такое коэффициент передачи? Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Или формулой:

U_вых — напряжение на выходе цепи

U_вх — напряжение на входе цепи

В усилительных устройствах коэффициент передачи больше единицы. Если устройство вносит ослабление передаваемого сигнала, то коэффициент передачи меньше единицы.

Коэффициент передачи может быть выражен через децибелы:

Строим АЧХ RC-цепи в программе Proteus

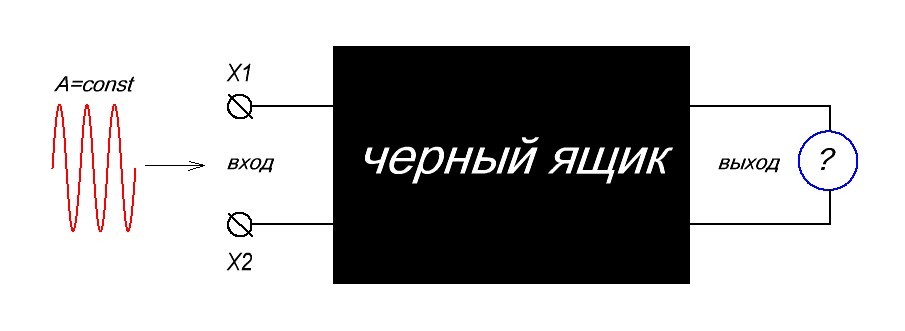
Для того, чтобы досконально разобраться, что такое АЧХ, давайте рассмотрим рисунок ниже.

Итак, имеем «черный ящик», на вход которого мы будем подавать синусоидальный сигнал, а на выходе черного ящика мы будем снимать сигнал. Должно соблюдаться условие: нужно менять частоту входного синусоидального сигнала, но его амплитуда должна быть постоянной.

Что нам делать дальше? Надо измерить амплитуду сигнала на выходе после черного ящика при интересующих нас значениях частоты входного сигнала. То есть мы должны изменять частоту входного сигнала от 0 Герц (постоянный ток) и до какого-либо конечного значения, которое будет удовлетворять нашим целям, и смотреть, какая амплитуда сигнала будет на выходе при соответствующих значениях на входе.

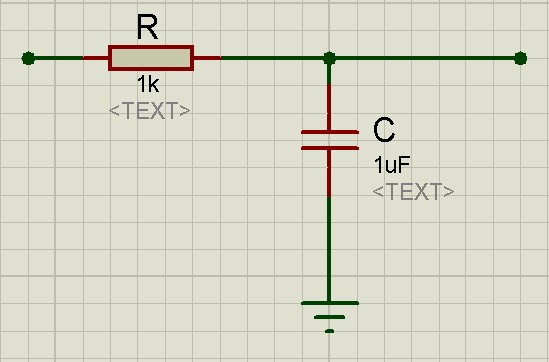
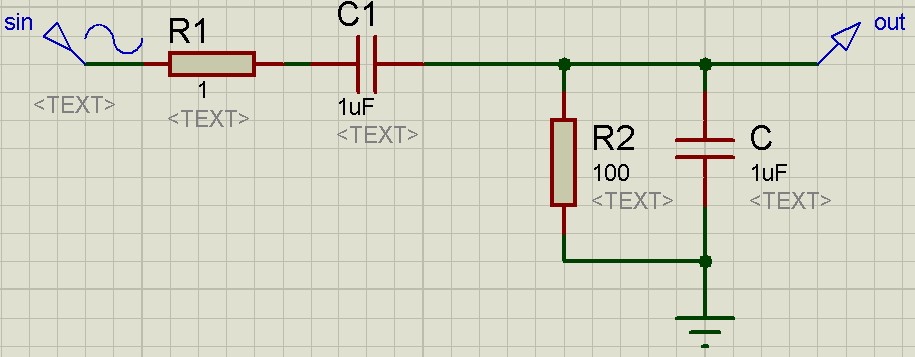
Давайте разберем все это дело на примере. Пусть в черном ящике у нас будет самая простая RC-цепь с уже известными номиналами радиоэлементов.

Как я уже говорил, АЧХ может быть построено экспериментально, а также с помощью программ-симуляторов. На мой взгляд, самый простой и мощный симулятор для новичков — это Proteus. С него и начнем.

Собираем данную схему в рабочем поле программы Proteus

Для того, чтобы подать на вход схемы синусоидальный сигнал, мы кликаем на кнопочку «Генераторы», выбираем SINE, а потом соединяем его со входом нашей схемы.

Для измерения выходного сигнала достаточно кликнуть на значок с буквой «V» и соединить выплывающий значок с выходом нашей схемы:

Для эстетики, я уже поменял название входа и выхода на sin и out. Должно получиться как-то вот так:

Ну вот, пол дела уже сделано.

Теперь осталось добавить важный инструмент. Он называется «frequency response», как я уже говорил, в дословном переводе с английского — «частотный отклик». Для этого нажимаем кнопочку «Диаграмма» и в списке выбираем «frequency»

На экране появится что-то типа этого:

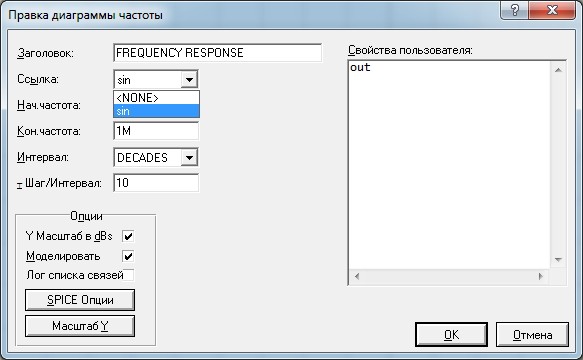
Кликаем ЛКМ два раза и открывается вот такое окошко, где в качестве входного сигнала мы выбираем наш генератор синуса (sin), который у нас сейчас задает частоту на входе.

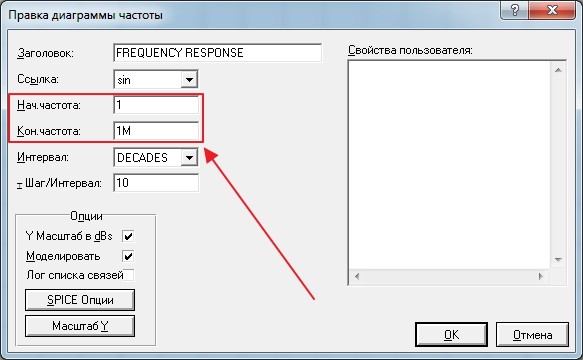
Здесь же выбираем диапазон частоты, который будем «загонять» на вход нашей цепи. В данном случае это диапазон от 1 Гц и до 1 МГц. При установке начальной частоты в 0 Герц Proteus выдает ошибку. Поэтому, ставьте начальную частоту близкую к нулю.

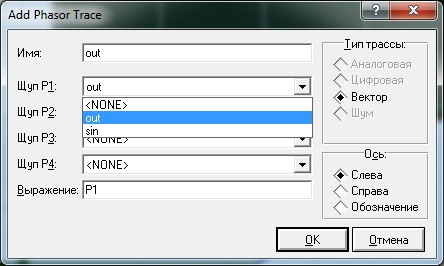
Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out

и в результате должно появится окошко с нашим выходом

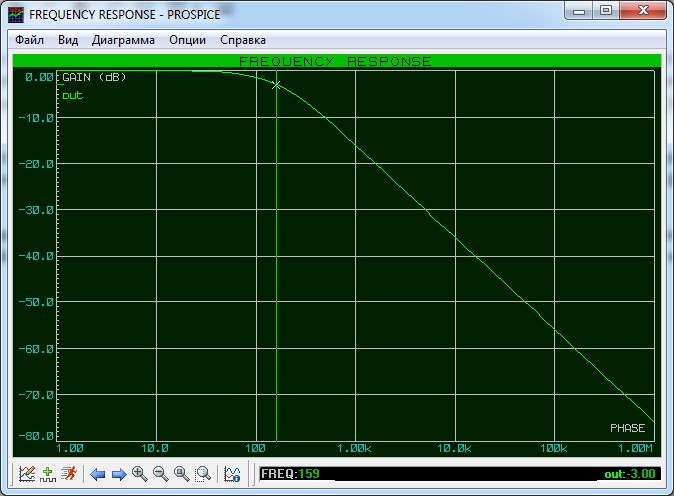
Нажимаем пробел и радуемся результату

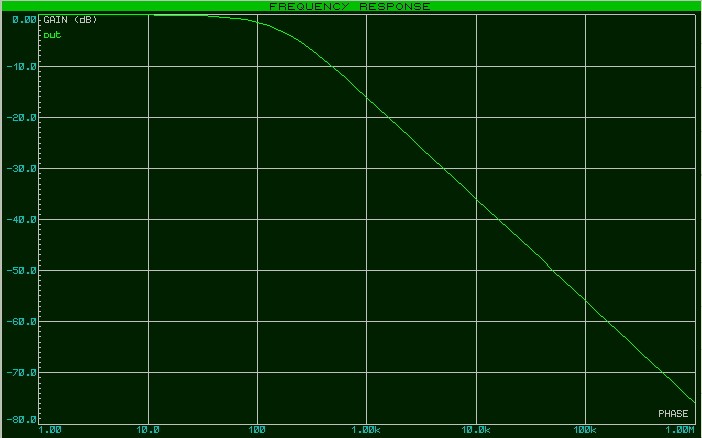
Итак, что интересного можно обнаружить, если взглянуть на нашу АЧХ? Как вы могли заметить, амплитуда на выходе цепи падает с увеличением частоты. Это означает, что наша RC-цепь является своеобразным частотным фильтром. Такой фильтр пропускает низкие частоты, в нашем случае до 100 Герц, а потом с ростом частоты начинает их «давить». И чем больше частота, тем больше он ослабляет амплитуду выходного сигнала. Поэтому, в данном случае, наша RC-цепь является самым простейшим фильтром низкой частоты (ФНЧ).

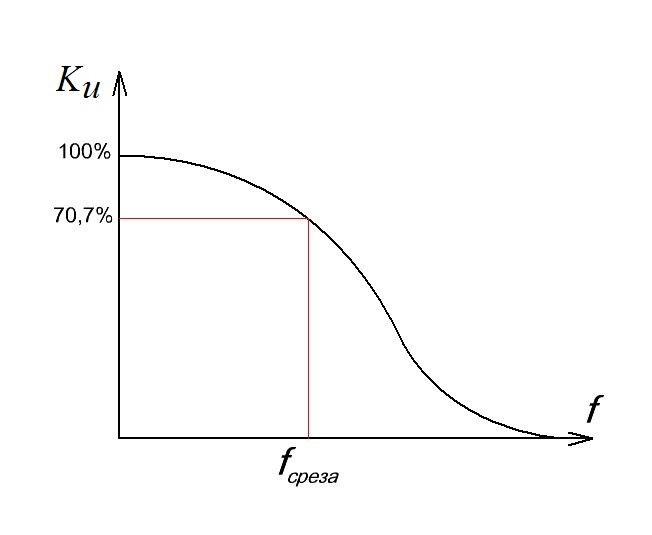
Полоса пропускания

В среде радиолюбителей и не только встречается также такой термин, как полоса пропускания. Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы.

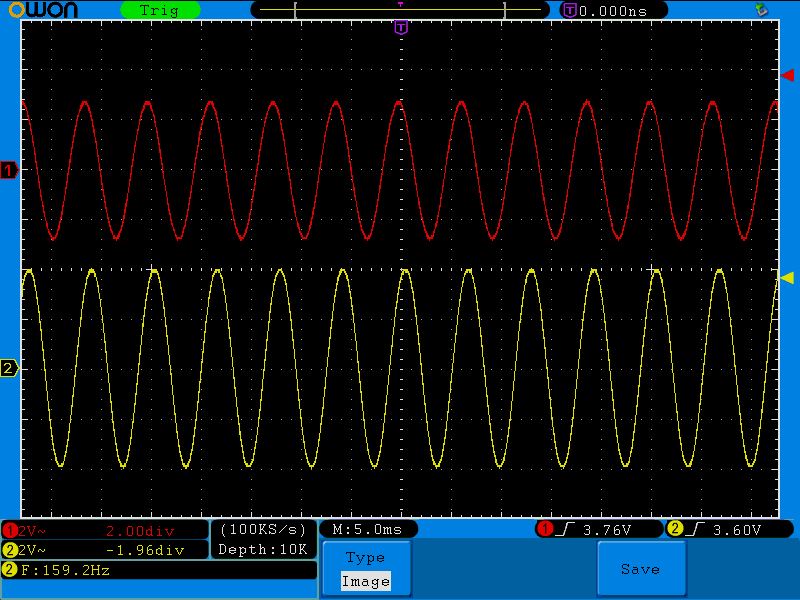
Как же определить полосу пропускания? Это сделать довольно легко. Достаточно на графике АЧХ найти уровень в -3 дБ от максимального значения АЧХ и найти точку пересечения прямой с графиком. В нашем случае это можно сделать легче пареной репы. Достаточно развернуть нашу диаграмму на весь экран и с помощью встроенного маркера посмотреть частоту на уровне в -3 дБ в точке пересечения с нашим графиком АЧХ. Как мы видим, она равняется 159 Герц.

Частота, которая получается на уровне в -3 дБ, называется частотой среза. Для RC-цепи ее можно найти по формуле:

Для нашего случая расчетная частота получилась 159,2 Гц, что подтверждает и Proteus.

Кто не желает связываться с децибелами, то можно провести линию на уровне 0,707 от максимальной амплитуды выходного сигнала и смотреть пересечение с графиком. В данном примере, для наглядности, я взял максимальную амплитуду за уровень в 100%.

Как построить АЧХ на практике?

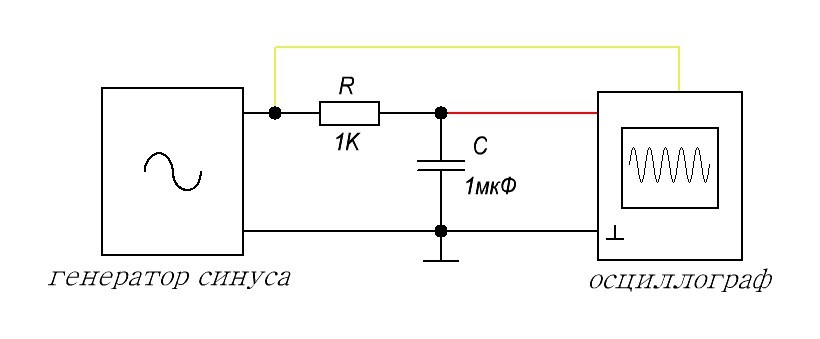
Как построить АЧХ на практике, имея в своем арсенале генератор частоты и осциллограф?

Итак, поехали. Собираем нашу цепь в реале:

Ну а теперь цепляем ко входу схемы генератор частоты, а с помощью осциллографа следим за амплитудой выходного сигнала, а также будем следить за амплитудой входного сигнала, чтобы мы были точно уверены, что на вход RC-цепи подается синус с постоянной амплитудой.

Для экспериментального изучения АЧХ нам потребуется собрать простенькую схемку:

Наша задача состоит в том, чтобы менять частоту генератора и уже наблюдать, что покажет осциллограф на выходе цепи. Мы будем прогонять нашу цепь по частотам, начиная от самой малой. Как я уже сказал, желтый канал предназначен для визуального контроля, что мы честно проводим опыт.

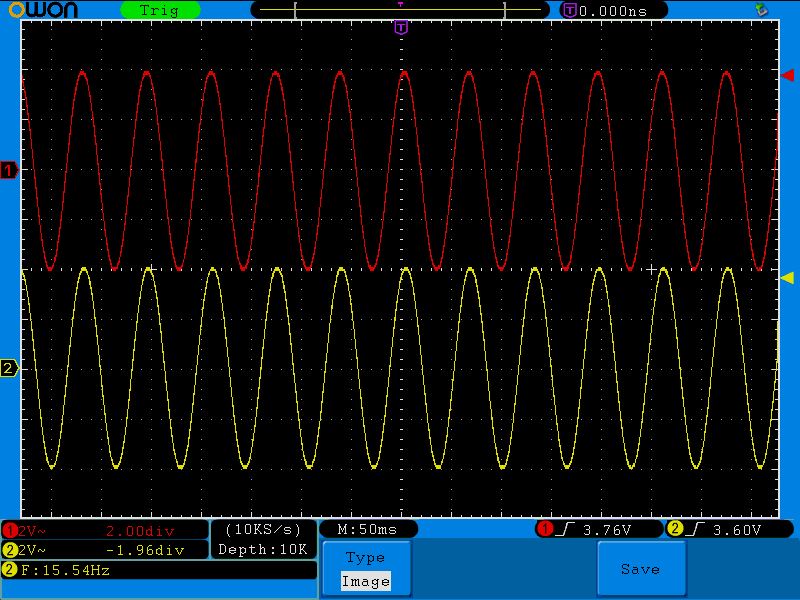
Постоянный ток, проходящий через эту цепь, на выходе будет давать амплитудное значение входного сигнала, поэтому первая точка будет иметь координаты (0;4), так как амплитуда нашего входного сигнала 4 Вольта.

Следующее значение смотрим на осциллограмме:

Частота 15 Герц, амплитуда на выходе 4 Вольта. Итак, вторая точка (15;4)

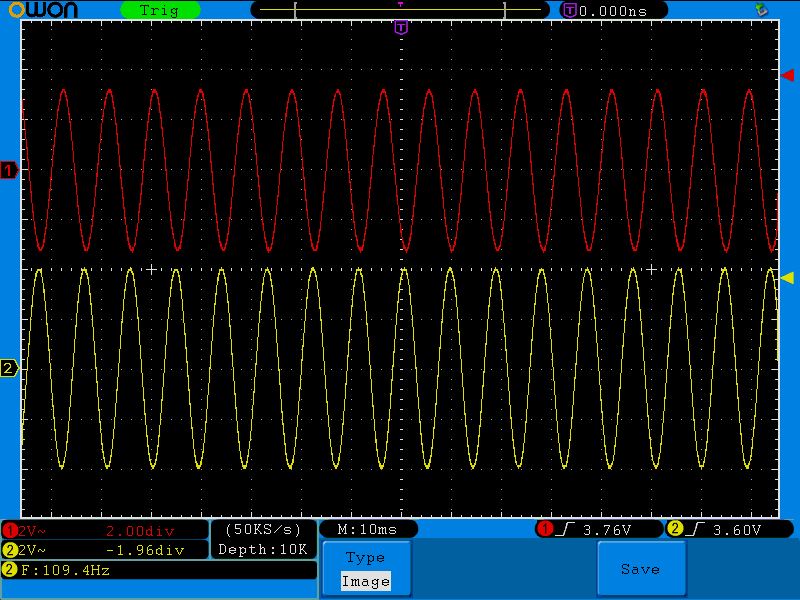
Третья точка (72;3.6). Обратите внимание на амплитуду выходного красного сигнала. Она начинает проседать.

Четвертая точка (109;3.2)

Пятая точка (159;2.8)

Шестая точка (201;2.4)

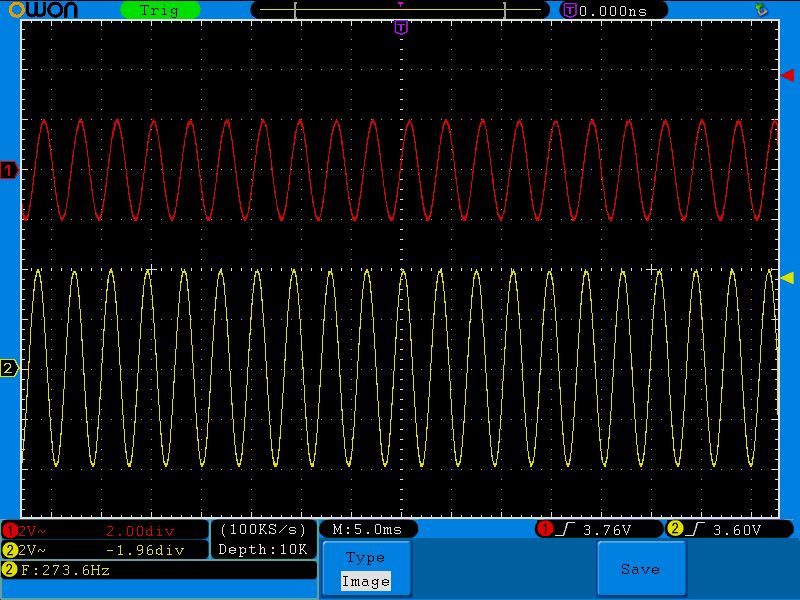
Седьмая точка (273;2)

Восьмая точка (361;1.6)

Девятая точка (542;1.2)

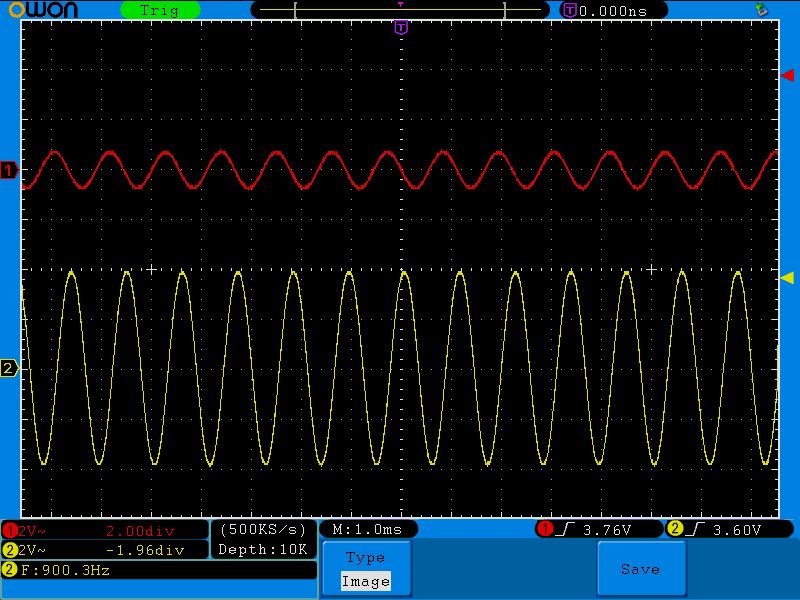
Десятая точка (900;0.8)

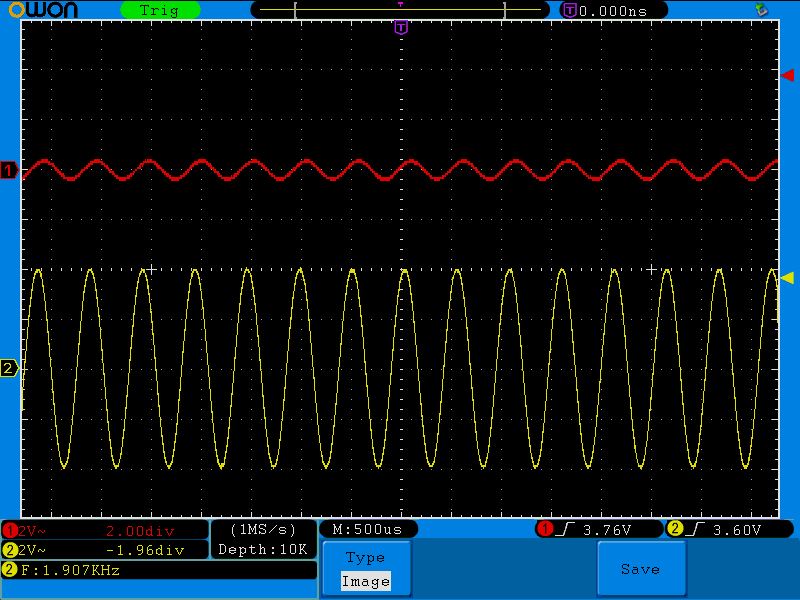
Ну и последняя одиннадцатая точка (1907;0.4)

В результате измерений у нас получилась табличка:

Строим график по полученным значениям и получаем нашу экспериментальную АЧХ 😉

Получилось не так, как в технической литературе. Оно и понятно, так как по Х берут логарифмический масштаб, а не линейный, как у меня на графике. Как вы видите, амплитуда выходного сигнала будет и дальше понижаться с увеличением частоты. Для того, чтобы еще более точно построить нашу АЧХ, требуется взять как можно больше точек.

Давайте вернемся к этой осциллограмме:

Здесь на частоте среза амплитуда выходного сигнала получилась ровно 2,8 Вольт, которые как раз и находятся на уровне в 0,707. В нашем случае 100% это 4 Вольта. 4х0,707=2,82 Вольта.

АЧХ полосового фильтра

Существуют также схемы, АЧХ которых имеет вид холма или ямы. Давайте рассмотрим один из примеров. Мы будем рассматривать так называемый полосовой фильтр, АЧХ которого имеет вид холма.

Собственно сама схема:

Особенность таких фильтров, что они имеют две частоты среза. Определяются они также на уровне в -3дБ или на уровне в 0,707 от максимального значения коэффициента передачи, а еще точнее K_{u max}/√2.

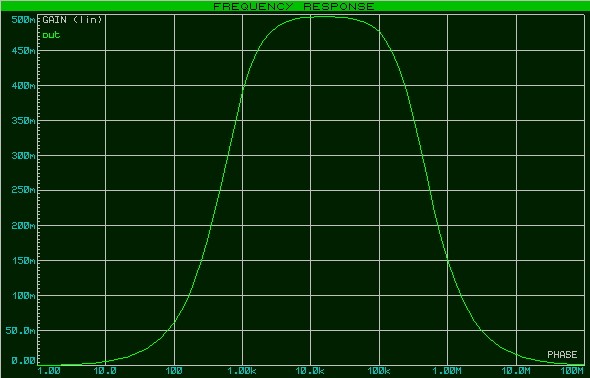
Так как в дБ смотреть график неудобно, поэтому я переведу его в линейный режим по оси Y, убирая маркер

В результате перестроения получилась такая АЧХ:

Максимальное значение на выходе составило 498 мВ при амплитуде входного сигнала в 10 Вольт. Мдя, неплохой «усилитель») Итак, находим значение частот на уровне в 0,707х498=352мВ. В результате получились две частоты среза — это частота в 786 Гц и в 320 КГц. Следовательно, полоса пропускания данного фильтра от 786Гц и до 320 КГц.

На практике для получения АЧХ используются приборы, называемые характериографами для исследования АЧХ. Вот так выглядит один из образцов Советского Союза

Видео:Амплитудно фазовая характеристикаСкачать

Фазо-частотная характеристика

ФЧХ расшифровывается как фазо-частотная характеристика, phase response — фазовый отклик. Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Разность фаз

Думаю, вы не раз слышали такое выражение, как » у него произошел сдвиг по фазе». Это выражение не так давно пришло в наш лексикон и обозначает оно то, что человек слегка двинулся умом. То есть было все нормально, а потом раз! И все :-). И в электронике такое тоже часто бывает) Разницу между фазами сигналов в электронике называют разностью фаз. Вроде бы «загоняем» на вход какой-либо сигнал, а выходной сигнал ни с того ни с сего взял и сдвинулся по времени, относительно входного сигнала.

Для того, чтобы определить разность фаз, должно выполняться условие: частоты сигналов должны быть равны. Пусть даже один сигнал будет с амплитудой в Киловольт, а другой в милливольт. Неважно! Лишь бы соблюдалось равенство частот. Если бы условие равенства не соблюдалось, то сдвиг фаз между сигналами все время бы изменялся.

Для определения сдвига фаз используют двухканальный осциллограф. Разность фаз чаще всего обозначается буквой φ и на осциллограмме это выглядит примерно так:

Строим ФЧХ RC-цепи в Proteus

Для нашей исследуемой цепи

Для того, чтобы отобразить ее в Proteus мы снова открываем функцию «frequency response»

Все также выбираем наш генератор

Не забываем проставлять испытуемый диапазон частот:

Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out

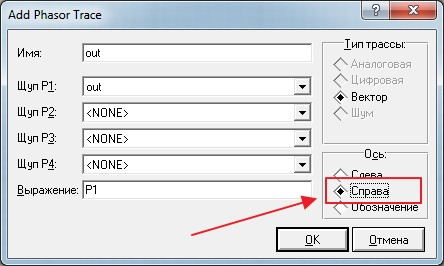
И теперь главное отличие: в колонке «Ось» ставим маркер на «Справа»

Нажимаем пробел и вуаля!

Можно его развернуть на весь экран

При большом желании эти две характеристики можно объединить на одном графике

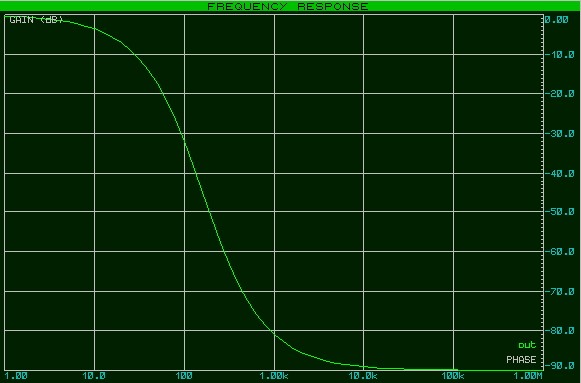
Обратите внимание, что на частоте среза сдвиг фаз между входным и выходным сигналом составляет 45 градусов или в радианах п/4 (кликните для увеличения)

В данном опыте при частоте более 100 КГц разность фаз достигает значения в 90 градусов (в радианах π/2) и уже не меняется.

Строим ФЧХ на практике

ФЧХ на практике можно измерить также, как и АЧХ, просто наблюдая разность фаз и записывая показания в табличку. В этом опыте мы просто убедимся, что на частоте среза у нас действительно разность фаз между входным и выходным сигналом будет 45 градусов или π/4 в радианах.

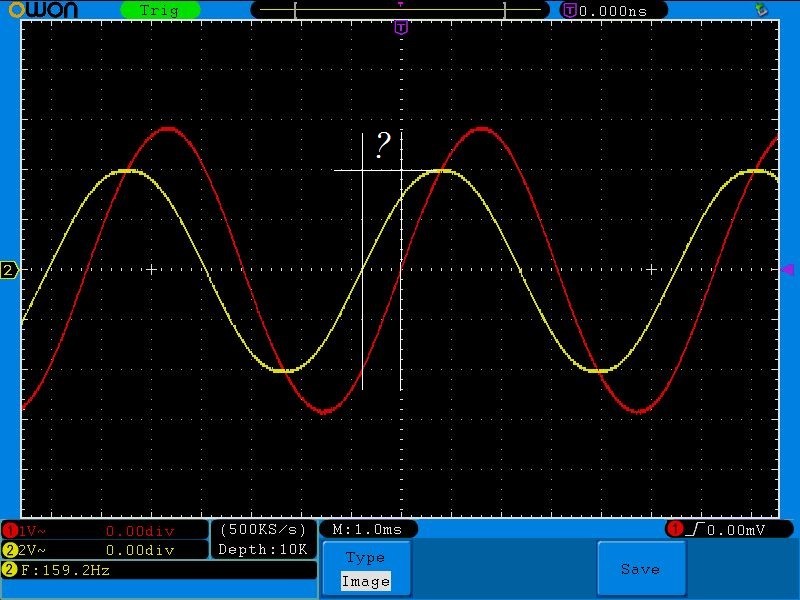
Итак, у меня получилась вот такая осциллограмма на частоте среза в 159,2 Гц

Нам надо узнать разность фаз между этими двумя сигналами

Весь период — это 2п, значит половина периода — это π. На полупериод у нас приходится где-то 15,5 делений. Между двумя сигналами разность в 4 деления. Составляем пропорцию:

Отсюда х=0,258п или можно сказать почти что 1/4п. Следовательно, разница фаз между двумя этими сигналами равняется п/4, что почти в точности совпало с расчетными значениями в Proteus.

Если Вы лучше воспринимаете информацию через видео, то к Вашему вниманию:

Видео:Теория автоматического регулирования. Лекция 4. Частотные характеристики САУСкачать

Резюме

Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.

Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Если коэффициент передачи больше единицы, то электрическая цепь усиливает входной ссигнал, если же меньше единицы, то ослабляет.

Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы. Определяется по уровню 0,707 от максимального значения АЧХ.

📽️ Видео

Частотные характеристики | Утро с теорией управления, лекция 5Скачать

Что такое АЧХ(Амплитудно Частотная Характеристика)Скачать

Частотное и временное представление сигналов. Спектр. МодуляцияСкачать

10) ТАУ для чайников Части 4.1. и 4.2. Типовые динамические звенья. Усилитель. Апериодическое звено.Скачать

23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

c04 3, Динамические звенья 2: типовые звенья и их АФЧХСкачать

Преобразования #7: амплитудный и фазовый спектры преобразования ФурьеСкачать

Расчёт и построение амплитудно-частотной и фазо-частотной характеристики RLC цепиСкачать

№10. Структурные схемы, уравнения и частотные характеристики стационарных линейных систем.Скачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Как построить асимптотическую ЛАФЧХ ч. 2Скачать

Теория автоматического управления. Лекция 7. Типовые звенья САУСкачать

AGalilov: Преобразование Фурье "на пальцах"Скачать