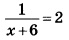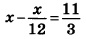Уравнения 9 класс огэ с ответами

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Задание №9 ОГЭ по математике

В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными. Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию. Ответом в задании №9 является целое число или конечная десятичная дробь.

Теория к заданию №9

Ниже я привел теорию по решениям линейных и квадратных уравнений:

Схема решения, правила и алгоритм действий при решении линейного уравнения:

Схема решения, правила и порядок действий при решении квадратного уравнения:

В трех типовых вариантах я разобрал данные случаи – в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем – решение полного квадратного уравнения с вычислением дискриминанта.

Найдите корень уравнения:

Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.

Для начала следует раскрыть скобки: 10x – 90 = 7

Затем переносим 90 в правую часть (не забываем поменять знак):

Затем делим обе части на 10:

pазбирался: Даниил Романович | обсудить разбор | оценить

Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:

Произведение множителей тогда равно нулю, когда один из множителей равен нолю:

Так как в ответе просят указать наименьший корень, то это -4.

pазбирался: Даниил Романович | обсудить разбор | оценить

Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:

Далее вычисляем дискриминант:

x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25

x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1

Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25

pазбирался: Даниил Романович | обсудить разбор | оценить

В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой – всё, что известно переносим в правую часть, всё, что неизвестно – оставляем в левой. Далее выполняем необходимое арифметическое действие.

Переносим 9 в правую часть (не забываем про смену знака):

7х = 40 + 9, что эквивалентно

х в нашем случае – это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите корень уравнения:

режде всего, исключим

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Выполним умножение в левой части уравнения и раскроем скобки справа:

Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:

Переносим 12 из левой части в правую:

ОДЗ это значение не исключает, поэтому оно является искомым результатом.Ответ: -5,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите корень уравнения:

Обе части уравнения приводим к единому знаменателю 12: 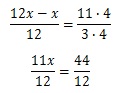Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем: 11х=44 х=44:11 х=4

pазбирался: Даниил Романович | обсудить разбор | оценить

Имеем линейное уравнение:

Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.

Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.

Запись решения выглядит так:

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:ОГЭ для НОЛИКОВ, Уравнения N-9Скачать

Задачник с ответами для подготовки к ОГЭ по математике ( задание № 9 , уравнения и системы уравнений)
материал для подготовки к егэ (гиа) по алгебре (9 класс)

Данная система заданий позволяет отработать навыки по решению задания № 9 ОГЭ по математике. Для проверки в конце сборника публикуются ответы.

Видео:Задание №9 на ОГЭ. Как решать уравнения? Какие типы будут?Скачать

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Система упражнений по теме: «Уравнения и системы уравнений».

В данном пособии предложена система упражнений с решениями по теме : «Уравнения и системы уравнений» для учащихся старшей школы.

Уравнения и системы уравнений

Элективный курс по алгебре в 9 классе по теме: «Уравнения и системы уравнений».

8 класс урок-зачёт по теме «Линейные уравнения и системы уравнений»

рассмотрены разные типы текстовых задач, которые решаются с помощью линейных уравнений и систем уравнений.

Урок-зачет в 10 классе по теме «Тригонометрические уравнения, неравенства, системы уравнений»

Цель урока: Проверить знания и умение применений формул для решения тригонометрических уравнений.Вид работы: «Смотр знаний», состоящий из 5 этапов, проводится в течение двух уроков. За каждый эт.

Программа прикладного курса по алгебре «Уравнения и системы уравнений»

Программа прикладного курса по алгебре «Уравнения и системы уравнений» для 11 класса.

Тест по алгебре для 9 класса с углубленным изучением математики по теме «СИСТЕМЫ УРАВНЕНИЙ И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ» .

Тест по алгебре для 9 класса с углубленным изучением математики по теме «СИСТЕМЫ УРАВНЕНИЙ И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ» .Задания теста соответствуют содержанию учебника «Алгебра. 9 .

Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.

Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.

Видео:Все типы задания 6 | Математика ОГЭ 2023 | УмскулСкачать

Алгебра. Урок 4. Уравнения, системы уравнений

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Линейные уравнения

Видео:Разбор реального варианта ОГЭ по математике 2024 на 5 за часСкачать

Линейные уравнения

Линейное уравнение – уравнение вида a x = b , где x – переменная, a и b некоторые числа, причем a ≠ 0 .

Примеры линейных уравнений:

1. 3 x = 2

1. 2 7 x = − 5

Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.

Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .

Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.

Для того, чтобы решить линейное уравнение , необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного линейного уравнения: x = b a .

Примеры решения линейных уравнений:

1. 2 x + 1 = 2 ( x − 3 ) + 8

Это линейное уравнение, так как переменная стоит в первое степени.

Попробуем преобразовать его к виду a x = b :

Для начала раскроем скобки:

2 x + 1 = 4 x − 6 + 8

В левую часть переносятся все слагаемые с x , в правую – числа:

Теперь поделим левую и правую часть на число ( -2 ) :

− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5

Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.

Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:

x 2 + 3 x − 8 = x − 1

Это уравнение не является линейным уравнением.

Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)

1. 2 x − 4 = 2 ( x − 2 )

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2 x − 2 x = − 4 + 4

И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2 x − 4 = 2 x − 16

2 x − 2 x = − 16 + 4

В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.

Видео:Как сдать ОГЭ по математике за 4 минуты? | УмскулСкачать

Квадратные уравнения

Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .

Алгоритм решения квадратного уравнения:

1. Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
2. Выписать, чему равны в числах коэффициенты: a = … b = … c = …
3. Вычислить дискриминант по формуле: D = b 2 − 4 a c
4. Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
5. Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
6. Если D 0, решений нет: x ∈ ∅

Примеры решения квадратного уравнения:

1. − x 2 + 6 x + 7 = 0

a = − 1, b = 6, c = 7

D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64

D > 0 – будет два различных корня:

x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7

Ответ: x 1 = − 1, x 2 = 7

a = − 1, b = 4, c = − 4

D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0

D = 0 – будет один корень:

x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2

a = 2, b = − 7, c = 10

D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31

D 0 – решений нет.

Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!

Видео:Задание №20. Уравнение 2 часть ОГЭ по математике 2023 | УмскулСкачать

Разложение квадратного трехчлена на множители

Квадратный трехчлен можно разложить на множители следующим образом:

a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )

где a – число, коэффициент перед старшим коэффициентом,

x – переменная (то есть буква),

x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.

Если квадратное уравнение имеет только один корень , то разложение выглядит так:

a x 2 + b x + c = a ⋅ ( x − x 0 ) 2

Примеры разложения квадратного трехчлена на множители:

1. − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7

− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )

1. − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2

− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2

Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:

• c = 0 ⇒ a x 2 + b x = x ( a x + b )

• b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.

Видео:Разбор реального варианта ОГЭ по математике 2023 | Математика ОГЭ 2023 | УмскулСкачать

Дробно рациональные уравнения

Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .

Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .

Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.

ОДЗ – область допустимых значений переменной.

В выражении вида f ( x ) g ( x ) = 0

ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).

Алгоритм решения дробно рационального уравнения:

1. Привести выражение к виду f ( x ) g ( x ) = 0 .
2. Выписать ОДЗ: g ( x ) ≠ 0.
3. Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
4. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Пример решения дробного рационального уравнения:

Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.

Решение:

Будем действовать в соответствии с алгоритмом.

1. Привести выражение к виду f ( x ) g ( x ) = 0 .

Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:

x 2 − 4 2 − x − 1 2 − x = 0

x 2 − 4 2 − x − 2 − x 2 − x = 0

x 2 − 4 − ( 2 − x ) 2 − x = 0

x 2 − 4 − 2 + x 2 − x = 0

x 2 + x − 6 2 − x = 0

Первый шаг алгоритма выполнен успешно.

Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2

1. Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:

x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.

a = 1, b = 1, c = − 6

D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25

D > 0 – будет два различных корня.

x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3

1. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Корни, полученные на предыдущем шаге:

Значит, в ответ идет только один корень, x = − 3.

Видео:ОГЭ по математике. Решаем уравнения | МатематикаСкачать

Системы уравнений

Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y ) , которые объединены в общую систему фигурной скобкой.

Пример системы уравнений

Решить систему уравнений – найти пару чисел x и y , которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.

Существует два метода решений систем линейных уравнений:

1. Метод подстановки.
2. Метод сложения.

Алгоритм решения системы уравнений методом подстановки:

1. Выразить из любого уравнения одну переменную через другую.
2. Подставить в другое уравнение вместо выраженной переменной полученное значение.
3. Решить уравнение с одной неизвестной.
4. Найти оставшуюся неизвестную.

Решить систему уравнений методом подстановки

Решение:

1. Выразить из любого уравнения одну переменную через другую.

1. Подставить в другое уравнение вместо выраженной переменной полученное значение.

1. Решить уравнение с одной неизвестной.

3 ( 8 − 2 y ) − y = − 4

y = − 28 − 7 = 28 7 = 4

1. Найти оставшуюся неизвестную.

x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0

Ответ можно записать одним из трех способов:

Решение системы уравнений методом сложения.

Метод сложения основывается на следующем свойстве:

Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.

Решить систему уравнений методом сложения

Давайте избавимся в данном примере от переменной x . Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3 . Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент ( − 3 ) . Для этого домножим левую и правую часть первого уравнения на ( − 3 ) .

Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.

( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )

− 3 x − 6 y + 3 x − y = − 24 − 4

y = − 28 − 7 = 28 7 = 4

Осталось найти переменную x . Для этого подставим y = 4 в любое из двух уравнений системы. Например, в первое.

Ответ можно записать одним из трех способов:

Видео:ВСЕ ТИПЫ 20 ЗАДАНИЕ 2 ЧАСТЬ ОГЭ МАТЕМАТИКА 2023Скачать

Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.

🌟 Видео

Сложные уравнения. Как решить сложное уравнение?Скачать

Задание 9 ОГЭ 2023 математика | Решаем уравненияСкачать

Линейные уравнения в ОГЭ | Математика ОГЭ 2022 | УмскулСкачать

Как решать уравнения на ОГЭ 2021? / Подробный разбор всех видов уравнений на ОГЭ по математикеСкачать

Разбор 1 вариант нового сборника Ященко Листы ОГЭ по математике 2024Скачать

Проверь свои знания по математике за 11 классСкачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Не сдал ОГЭ Устное Собеседование shorts #shortsСкачать