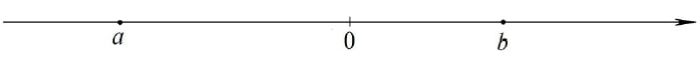Решение и ответы заданий демонстрационного варианта ВПР 8 класс по математике. Образец всероссийской проверочной работы 2022 год.
Задание 1.
Найдите значение выражения
ИЛИ
Найдите значение выражения 4,5·5,4 – 6,1
Задание 2.
Решите уравнение (5х – 2)(–х + 3) = 0
Задание 3.
Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 72 га и распределена между зерновыми и зернобобовыми культурами в отношении 7 : 2 соответственно. Сколько гектаров занимают зернобобовые культуры?
Задание 4.
На координатной прямой отмечены числа a и b. Отметьте на прямой какую-нибудь точку x так, чтобы при этом выполнялись три условия: x – a > 0, x – b 2 x > 0.
Задание 5.
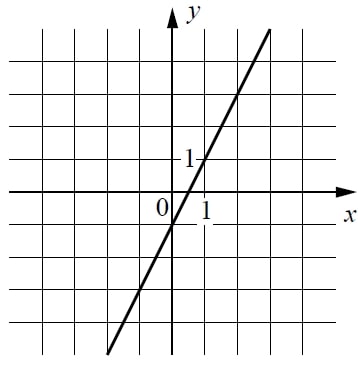
На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию.
Задание 6.
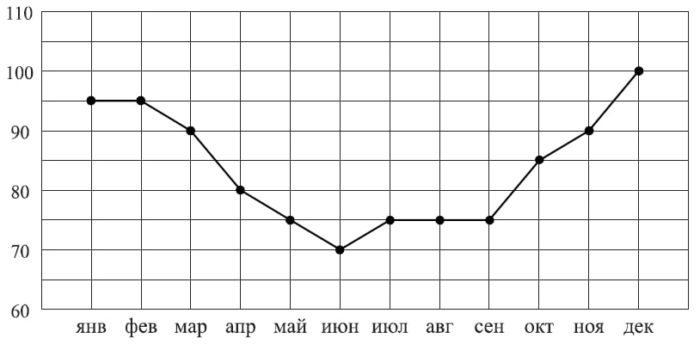
Потребление электроэнергии измеряется в киловатт-часах ( кВт⋅ч). Жирными точками показано потребление электроэнергии в некоторой стране в течение 2016 года в миллиардах кВт⋅ч. Для наглядности точки соединены линиями. Данные округлены до 5 млрд кВт⋅ч.
На диаграмме видно, что потребление электроэнергии в середине года существенно ниже, чем в начале и конце года. Чем это можно объяснить? Можно ли предположить, в каком полушарии находится эта страна – в Южном или в Северном? Можно ли что-то сказать о том, суровые ли зимы в этой стране? Напишите два-три предложения, в которых кратко выскажите и обоснуйте своё мнение по этим вопросам.
Задание 7.
На соревнованиях по фигурному катанию каждый элемент имеет базовую стоимость и судейскую оценку. Девять судей независимо друг от друга выставляют за каждый элемент свои оценки от –5 до +5 баллов. Затем самая высокая и самая низкая оценки отбрасываются. Среднее арифметическое оставшихся семи оценок, округлённое до сотых, прибавляется к базовой стоимости. Полученная сумма является итоговой оценкой за элемент. Фигуристу Артёму Петрову судьи поставили оценки за три элемента. Эти оценки и базовая стоимость каждого элемента показаны в таблице. Определите, за какой элемент Артём Петров получил наиболее высокую оценку. В ответе запишите этот элемент и оценку за него.
Задание 8.
Отметьте на координатной прямой числа √10 и √34
Задание 9.
Найдите значение выражения при х = √3, y = –5,2.
Задание 10.
На фестивале выступают группы – по одной от каждой из заявленных стран, среди этих стран Румыния, Болгария и Греция. Порядок выступления определяется жребием. Какова вероятность того, что группа из Румынии будет выступать до группы из Болгарии, но после группы из Греции?
Задание 11.
Свежие абрикосы содержат 88% воды, а сушеные абрикосы (курага) – 30%. Сколько требуется свежих абрикосов для приготовления 72 кг кураги?
Задание 12.
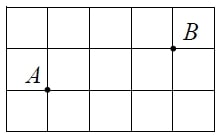
На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. Найдите расстояние между этими точками.
Задание 13.
Дан треугольник ABC. Известно, что AB = BC = 25, AC = 40. Найдите синус угла A.
Задание 14.
Укажите номер верного утверждения.
1) Если в параллелограмме две стороны равны, то такой параллелограмм является ромбом.
2) Если в четырёхугольнике две диагонали равны и перпендикулярны, то такой четырёхугольник — квадрат.
3) Если в ромбе диагонали равны, то такой ромб является квадратом.
4) Углы при меньшем основании трапеции тупые.
Задание 15.
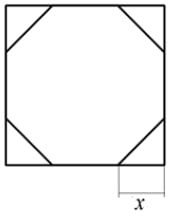
У стекольщика есть квадратное стекло. Сторона квадрата равна 40 см. Нужно вырезать из этого стекла восьмиугольник, у которого все стороны равны и все углы равны. Для этого нужно наметить линии и по этим линиям отрезать от квадрата четыре одинаковых прямоугольных треугольника по углам (см. рисунок). Найдите приближённо длину катета одного такого треугольника в миллиметрах, считая, что √2 равен 1,41.
Запишите решение и ответ.
Задание 16.
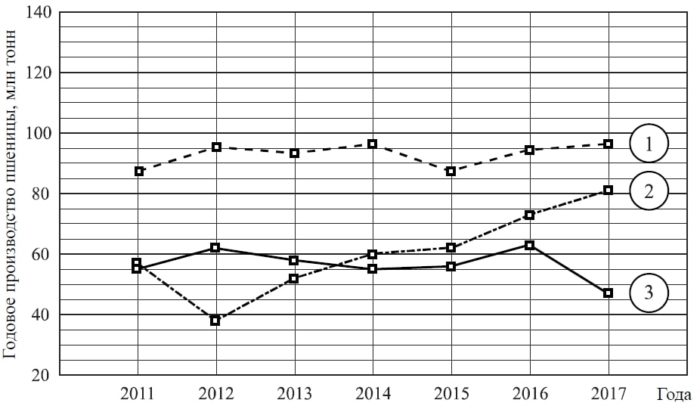
Годовое производство пшеницы – это суммарная масса всех сортов пшеницы, выращенной в стране в течение года. Обычно измеряется в млн тонн. На диаграмме показано производство пшеницы в млн тонн в России, США и Индии за семь лет начиная с 2011 года. Рассмотрите диаграмму и прочтите фрагмент сопровождающей статьи.
В 2012 году на основных хлебородных территориях России случилась аномальная засуха. Она повсеместно нанесла значительный ущерб посевам пшеницы, а на 8% площадей полностью погубила урожай. Погодные условия мешали не только российским хлеборобам.
В 2015 году в Индии длительная жара привела к выгоранию части площадей, занятых пшеницей. Кроме того, на урожайности пшеницы в Индии в том году негативно сказались чрезмерные осадки и град, последовавшие за засухой.
В США из-за падения закупочных цен на пшеницу в 2017 году фермеры сократили на 1,5 млн га посевные площади, отведённые под пшеницу. Засуха и поздние метели в США в том же году стали причиной рекордно низкой урожайности зерновых.
В Китайской Народной Республике в большинстве хлебородных районов на протяжении последних десяти лет погода благоприятствовала сельскому хозяйству. Постепенно повышающаяся культура земледелия в КНР способствует небыстрому устойчивому росту производства пшеницы, составляющей наряду с рисом основу рациона населения. В 2015 году урожай составил 130 млн тонн – на 10 млн тонн больше, чем четырьмя годами раньше. Однако 2016 год оказался менее удачным и суммарный урожай снизился на 2 млн тонн по сравнению с 2015 годом. Но уже в 2017 году снова наблюдался резкий рост по сравнению с прошлым годом, а суммарный урожай пшеницы в 2017 году оказался на 10% выше, чем в 2011 году.
1) На основании прочитанного определите, какой стране соответствует каждый из трёх графиков.
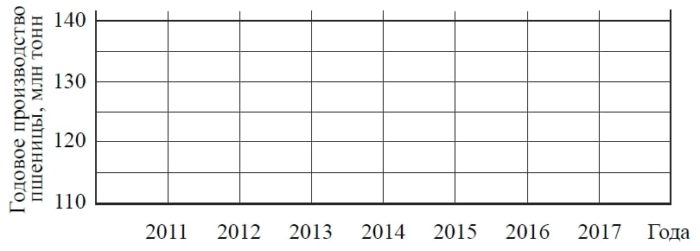
2) По имеющемуся описанию постройте схематично график производства пшеницы в Китае в 2011–2017 гг.
Задание 17.
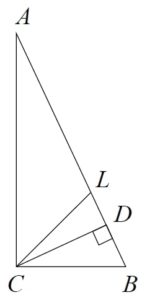
В прямоугольном треугольнике ABC с гипотенузой AB провели высоту CD и биссектрису CL. Найдите величину угла DCL, если ∠CAB = 25°. Ответ дайте в градусах. Запишите решение и ответ.
Задание 18.
Расстояние между пунктами А и В по реке равно 45 км. Из А в В одновременно отправились плот и моторная лодка. Моторная лодка, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 28 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Запишите решение и ответ.
Задание 19.
Сумма ста натуральных чисел равна 5000. Все эти числа разбили на три группы, причём во всех группах разное количество чисел. Известно, что:
– в первой группе 29 чисел, их среднее арифметическое равно 21;
– среднее арифметическое чисел второй группы равно 50;
– среднее арифметическое чисел третьей группы – целое число.
Найдите количество чисел в третьей группе.
Запишите решение и ответ.
- Реальные варианты ВПР 2021 по математике 8 класс с ответами
- ПОДЕЛИТЬСЯ
- Варианты ВПР 2021 по математике 8 класс с ответами:
- Вариант №1 ВПР 2021 по математике 8 класс с ответами
- Вариант №2 ВПР 2021 по математике 8 класс с ответами
- Вариант №3 ВПР 2021 по математике 8 класс с ответами
- Вариант №4 ВПР 2021 по математике 8 класс с ответами
- Вариант №5 ВПР 2021 по математике 8 класс с ответами
- Вариант №6 ВПР 2021 по математике 8 класс с ответами
- Вариант №7 ВПР 2021 по математике 8 класс с ответами
- Вариант №8 ВПР 2021 по математике 8 класс с ответами
- Вариант №9 ВПР 2021 по математике 8 класс с ответами
- Вариант №10 ВПР 2021 по математике 8 класс с ответами
- Вариант №11 ВПР 2021 по математике 8 класс с ответами
- Вариант №12 ВПР 2021 по математике 8 класс с ответами
- Вариант №13 ВПР 2021 по математике 8 класс с ответами
- Вариант №14 ВПР 2021 по математике 8 класс с ответами
- Вариант №15 ВПР 2021 по математике 8 класс с ответами
- Вариант №16 ВПР 2021 по математике 8 класс с ответами
- Вариант №17 ВПР 2021 по математике 8 класс с ответами
- Вариант №18 ВПР 2021 по математике 8 класс с ответами
- Вариант №19 ВПР 2021 по математике 8 класс с ответами
- Вариант №20 ВПР 2021 по математике 8 класс с ответами
- Интересные задания и ответы с вариантов ВПР:
- ВПР по математике 8 класс 2021 Варианты с ответами
- 🌟 Видео
Видео:Алгебра 8 класс с нуля | Математика ОГЭ 2023 | УмскулСкачать

Реальные варианты ВПР 2021 по математике 8 класс с ответами
ПОДЕЛИТЬСЯ
ВПР 2021 по математике 8 класс официальные задания с ответами реальных вариантов всероссийской проверочной работы для проведения с 15 марта по 21 мая 2021 года.
P.S дату проведения ВПР школа выбирает самостоятельно
На выполнение работы по математике даётся 90 минут. Работа содержит 19 заданий. В заданиях, после которых есть поле со словом «Ответ», запишите ответ в указанном месте. В заданиях, после которых есть поле со словами «Решение» и «Ответ», запишите решение и ответ в указанном месте. В заданиях 4 и 8 нужно отметить точки на числовой прямой.
Варианты ВПР 2021 по математике 8 класс с ответами:
Вариант №1 ВПР 2021 по математике 8 класс с ответами
Вариант №2 ВПР 2021 по математике 8 класс с ответами
Вариант №3 ВПР 2021 по математике 8 класс с ответами
Вариант №4 ВПР 2021 по математике 8 класс с ответами
Вариант №5 ВПР 2021 по математике 8 класс с ответами
Вариант №6 ВПР 2021 по математике 8 класс с ответами
Вариант №7 ВПР 2021 по математике 8 класс с ответами
Вариант №8 ВПР 2021 по математике 8 класс с ответами
Вариант №9 ВПР 2021 по математике 8 класс с ответами
Вариант №10 ВПР 2021 по математике 8 класс с ответами
Вариант №11 ВПР 2021 по математике 8 класс с ответами
Вариант №12 ВПР 2021 по математике 8 класс с ответами
Вариант №13 ВПР 2021 по математике 8 класс с ответами
Вариант №14 ВПР 2021 по математике 8 класс с ответами
Вариант №15 ВПР 2021 по математике 8 класс с ответами
Вариант №16 ВПР 2021 по математике 8 класс с ответами
Вариант №17 ВПР 2021 по математике 8 класс с ответами
Вариант №18 ВПР 2021 по математике 8 класс с ответами
Вариант №19 ВПР 2021 по математике 8 класс с ответами
Вариант №20 ВПР 2021 по математике 8 класс с ответами
Интересные задания и ответы с вариантов ВПР:
1)В спортивном зале находятся футбольные и волейбольные мячи. Число футбольных мячей относится к числу волейбольных как 4:8. Сколько всего мячей в спортивном зале, если волейбольных мячей 24?
2)Соревнования по фигурному катанию проходят 3 дня. Всего запланировано 50 выступлений: в первый день — 14 выступлений, остальные распределены поровну между вторым и третьим днями. В соревнованиях участвует спортсмен Н. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что спортсмен Н. будет выступать в последний день соревнований?
3)Турист прошёл 20% всего маршрута, а затем 25% оставшегося расстояния. Сколько километров нужно ещё пройти туристу, если длина всего маршрута составляет 132 км?
4)Выберите верное утверждение и запишите в ответе его номер. 1) Диагональ трапеции делит её на два равных треугольника. 2) В тупоугольном треугольнике все углы тупые. 3) Существуют три прямые, которые проходят через одну точку.
5)Механический одометр (счётчик пройденного пути) для велосипеда — это прибор, который крепится на руле и соединён тросиком с редуктором, установленным на оси переднего колеса. При движении велосипеда спицы колеса вращают редуктор, это вращение по тросику передаётся счётчику, который показывает пройденное расстояние в километрах. У Димы был велосипед с колёсами диаметром 24дюйма и с одометром, который был настроен под данный диаметр колеса. Когда Дима вырос, ему купили дорожный велосипед с колёсами диаметром 28 дюймов. Дима переставил одометр со своего старого велосипеда на новый, но не настроил его под диаметр колеса нового велосипеда. В воскресенье Дима поехал кататься на велосипеде в парк. Когда он вернулся, одометр показал пройденное расстояние — 13,2 км. Какое расстояние на самом деле проехал Дима?
6)Мотоциклист выехал из пункта А в пункт В. Проехав весь путь с постоянной скоростью, он отправился обратно со скоростью больше прежней на 9 км/ч. Проехав половину обратного пути, он уменьшил скорость до 30 км/ч, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость мотоциклиста на пути из А в В. Ответ дайте в км/ч. Запишите решение и ответ
7)В многоподъездном доме в каждом подъезде одинаковое число этажей, а на каждом этаже по 6 квартир. Петя живёт в третьем подъезде на шестом этаже в квартире № 238. Даша живёт в пятом подъезде того же дома и тоже на шестом этаже. Какой номер квартиры у Даши, если он делится на число этажей дома без остатка?
8)В школе открыты две спортивные секции: по футболу и по лёгкой атлетике. Заниматься можно только в одной из них. Число школьников, занимающихся в секции по футболу, относится к числу школьников, занимающихся в секции по лёгкой атлетике, как 11:8. Сколько школьников занимаются в секции по футболу, если всего в двух секциях занимаются 57 школьников?
9)На диаграмме жирными точками показан расход электроэнергии в однокомнатной квартире в период с января по декабрь 2018 года в кВт ч⋅ . Для наглядности точки соединены линией. На сколько примерно киловатт-часов больше было израсходовано в сентябре, чем в августе? Чем, по вашему мнению, можно объяснить снижение расхода электроэнергии в летний период? Напишите несколько предложений, в которых обоснуйте своё мнение по этому вопросу.
10)Вероятность того, что за год в гирлянде перегорит хотя бы одна лампочка, равна 0,97. Вероятность того, что перегорит больше двух лампочек, равна 0,92. Найдите вероятность того, что за год перегорит одна или две лампочки.
11)Товар на распродаже уценили на 30%, а затем ещё на 15%. Сколько рублей стал стоить товар, если до распродажи он стоил 1800 рублей?
12)Выберите неверные утверждения и запишите в ответе их номера. 1) Все углы прямоугольника равны. 2) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника. 3) Если две параллельные прямые пересечены третьей, то сумма накрест лежащих углов всегда равна 180°.
13)Пассажирский поезд, двигаясь со скоростью 30 км/ч, полностью проезжает туннель за 90 секунд. Сколько метров составляет длина этого туннеля, если длина поезда 600 метров?
14)На товарищеском турнире школьников по шахматам каждый школьник сыграл с каждым другим не более одной партии, кроме того, каждый из них сыграл с приглашённым гроссмейстером не более одной партии. Всего было сыграно 40 партий. Какое наименьшее количество школьников могло участвовать в этом турнире?
15)В аквариуме плавают сомики и радужницы. Число сомиков относится к числу радужниц как 4:5. Сколько сомиков в этом аквариуме, если радужниц в нём 20?
16)При изготовлении шоколадных батончиков номинальной массой 60 г вероятность того, что масса батончика будет в пределах от 59 г до 61 г, равна 0,57. Найдите вероятность того, что масса батончика отличается от номинальной больше чем на 1 г.
17)Бак автомобиля вмещает 90 л бензина. Перед поездкой бак был заполнен бензином наполовину. За время поездки было израсходовано 40% бензина. Сколько литров бензина нужно долить, чтобы бак стал полным?
18)Выберите неверное утверждение и запишите в ответе его номер. 1) Существуют две различные точки плоскости, через которые нельзя провести прямую. 2) Если один из углов равнобедренного треугольника равен 120°, то другой его угол равен 30°. 3) Центром окружности, описанной около правильного треугольника, является точка пересечения его высот.
19)Два каменщика укладывают плиткой два одинаковых участка мостовой, каждый площадью 420 2 м . Первый каменщик в день укладывает на 7 2 м плитки больше, чем второй, и выполняет всю работу на 5 дней быстрее. Сколько квадратных метров плитки укладывает в день первый каменщик?
20)По бортику круглого цветочного горшка ползут гусеница и улитка в одном направлении с постоянными скоростями. Когда за ними начал наблюдать Игорь, они были в диаметрально противоположных точках бортика. Время от времени гусеница обгоняет улитку. Третий обгон произошёл через 12 минут после начала наблюдения. Через сколько минут после третьего обгона произойдёт четвёртый?
21)В спортивном зале находятся футбольные и волейбольные мячи. Число футбольных мячей относится к числу волейбольных как 5:9. Сколько всего мячей в спортивном зале, если волейбольных мячей 45?
22)На диаграмме жирными точками показан расход электроэнергии в трёхкомнатной квартире в период с января по декабрь 2018 года в кВт ч⋅ . Для наглядности точки соединены линией. На сколько примерно киловатт-часов больше было израсходовано в сентябре, чем в августе? Чем, по вашему мнению, можно объяснить снижение расхода электроэнергии в летний период? Напишите несколько предложений, в которых обоснуйте своё мнение по этому вопросу. На сколько примерно киловатт часов больше было израсходовано в сентябре, чем в августе? Чем, по вашему мнению, можно объяснить снижение расхода электроэнергии в летний период? Напишите несколько предложений, в которых обоснуйте своё мнение по этому вопросу.
23)В таблице указано содержание витаминов (в миллиграммах) в 100 г фруктов. Какое наименьшее количество граммов киви содержит не менее 0,3 мг витамина Е и 150 мг витамина С?
24)Вероятность того, что за год в гирлянде перегорит хотя бы одна лампочка, равна 0,98. Вероятность того, что перегорит больше трёх лампочек, равна 0,91. Найдите вероятность того, что за год перегорит не меньше одной, но не больше трёх лампочек.
25)Турист прошёл 30% всего маршрута, а затем 20% оставшегося расстояния. Сколько километров нужно ещё пройти туристу, если длина всего маршрута составляет 85 км?
26)Выберите верные утверждения и запишите в ответе их номера. 1) Существуют две различные прямые, не имеющие общих точек. 2) Если расстояние между центрами двух окружностей больше суммы их радиусов, то эти окружности касаются. 3) Диагонали равнобедренной трапеции равны.
27)Моторная лодка прошла против течения реки 176 км и вернулась в пункт отправления, затратив на обратный путь на 3 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч. Ответ дайте в км/ч. Запишите решение и ответ.
28)В среднем 28 керамических горшков из 200 после обжига имеют дефекты. Найдите вероятность того, что случайно выбранный после обжига горшок не имеет дефекта.
29)Выберите неверное утверждение и запишите в ответе его номер. 1) Равнобедренный треугольник всегда является остроугольным. 2) Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник. 3) Любые два диаметра окружности пересекаются.
30)Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 30 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 9 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
31)В цветнике растут только крокусы и нарциссы. Крокусы составляют пять девятых всех растений цветника, а нарциссов растёт 20 штук. Сколько всего растений в цветнике?
32)В коробке лежат одинаковые на вид шоколадные конфеты: 7 с карамелью, 6 с орехами и 7 без начинки. Миша наугад выбирает одну конфету. Найдите вероятность того, что он выберет конфету без начинки.
33)Выберите верное утверждение и запишите в ответе его номер. 1) В параллелограмме сумма противолежащих углов равна 180°. 2) Если при пересечении двух прямых третьей соответственные углы равны, то эти две прямые перпендикулярны. 3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
34)В классе 27 учащихся. Известно, что среди любых 14 учащихся имеется хотя бы одна девочка, а среди любых 15 учащихся — хотя бы один мальчик. Сколько мальчиков в классе? Запишите решение и ответ.
35)В среднем 5 керамических горшков из 250 после обжига имеют дефекты. Найдите вероятность того, что случайно выбранный после обжига горшок не имеет дефекта.
36)Турист прошёл 35% всего маршрута, а затем 20% оставшегося расстояния. Сколько километров нужно ещё пройти туристу, если длина всего маршрута составляет 105 км?
37)Выберите неверные утверждения и запишите в ответе их номера. 1) Если угол равен 60°, то вертикальный ему угол равен 30°. 2) Если все стороны параллелограмма равны, то этот параллелограмм является ромбом. 3) Все хорды одной окружности равны между собой.
38)Два велосипедиста одновременно отправляются в 100-километровый пробег. Первый едет со скоростью на 15 км/ч большей, чем второй, и прибывает к финишу на 6 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
39)На доске написано 48 различных целых чисел. Каждое число возвели либо в квадрат, либо в куб и результат записали вместо первоначального числа. Какое наименьшее количество различных чисел могло оказаться записано на доске?
40)На диаграмме жирными точками показано количество мороженого, произведённого в России в каждом месяце с января по октябрь 2017 года, в тоннах. Для наглядности точки соединены линией. По диаграмме видно, что производство мороженого в некоторые месяцы выше, чем в другие. Чем это можно объяснить? Сделайте предположение о том, в каких регионах нашей страны и в какие месяцы самое высокое потребление мороженого. Напишите несколько предложений, в которых обоснуйте своё мнение по этому вопросу.
41)Бак автомобиля вмещает 95 л бензина. Перед поездкой бак был заполнен бензином на 80%. За время поездки было израсходовано 25% бензина. Сколько литров бензина нужно долить, чтобы бак стал полным?
42)Выберите верные утверждения и запишите в ответе их номера. 1) Если расстояние от центра окружности до прямой равно диаметру окружности, то прямая касается окружности. 2) Если при пересечении двух данных прямых третьей внутренние накрест лежащие углы равны, то данные прямые параллельны. 3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
43)Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите периметр параллелограмма ABCD, если АB = 7. Запишите решение и ответ.
44)Путь длиной 34 км первый велосипедист проезжает на 50 минут дольше второго. Найдите скорость второго велосипедиста, если известно, что она на 5 км/ч больше скорости первого. Ответ дайте в км/ч. Запишите решение и ответ.
45)Дима написал пять натуральных (необязательно различных) чисел, а потом Варя вычислила все возможные попарные суммы этих чисел. Получилось всего три различных значения: 55, 74 и 93. Посмотрев на полученные Варей значения, Максим смог точно назвать наибольшее из написанных Димой чисел. Какое это число? Запишите решение и ответ.
46)На кружок по математике записались семиклассники и восьмиклассники. Количество семиклассников, записавшихся на кружок, относится к количеству восьмиклассников как 3:5 соответственно. Сколько всего школьников записалось на кружок по математике, если среди них 9 семиклассников?
47)Вероятность того, что за год в гирлянде перегорит больше одной лампочки, равна 0,97. Вероятность того, что перегорит больше четырёх лампочек, равна 0,86. Найдите вероятность того, что за год перегорит больше одной, но не больше четырёх лампочек.
48)Натуральное число сначала увеличили на 20%, а потом результат уменьшили на 45%, получилось число 1452. Найдите исходное натуральное число
49)Велосипед приводится в движение с помощью двух звёздочек и цепи, натянутой между ними (см. рис.). Велосипедист вращает педали, которые закреплены на передней звёздочке, далее усилие с помощью цепи передаётся на заднюю звёздочку, которая вращает заднее колесо. На передней звёздочке велосипеда 42 зубца, на задней — 14. Диаметр заднего колеса равен 65 см. Какое расстояние проедет велосипед за один полный оборот педалей? При расчёте округлите π до 3,14. Результат округлите до десятых долей метра.
50)Двое рабочих одновременно начали выполнять два одинаковых заказа, состоящих из одинакового количества деталей. Первый рабочий выполнял весь заказ равномерно, изготавливая определённое число деталей в день. Второй сначала изготавливал на 11 деталей в день меньше, чем делал первый рабочий, а когда выполнил половину заказа, то стал делать по 66 деталей в день, в результате чего закончил работу одновременно с первым. Какое количество деталей в день делал первый рабочий, если известно, что оно больше 40? Запишите решение и ответ.
51)Дети водят хоровод вокруг новогодней ёлки. Все девочки нарядились принцессами, а все мальчики мушкетёрами. Рядом с каждым мушкетёром обязательно есть хотя бы одна принцесса. Какое наибольшее число мушкетёров может быть в хороводе, если всего детей 37? Свой ответ обоснуйте. Запишите решение и ответ.
52)Соревнования по фигурному катанию проходят 4 дня. Всего запланировано 50 выступлений: в первые два дня — по 12 выступлений, остальные распределены поровну между третьим и четвёртым днями. В соревнованиях участвует спортсмен Л. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что спортсмен Л. будет выступать в третий день соревнований?
53)Товар на распродаже уценили на 15%, а затем ещё на 20%. Сколько рублей стал стоить товар, если до распродажи он стоил 2200 рублей?
54)Выберите верные утверждения и запишите в ответе их номера. 1) Если три угла четырёхугольника равны 40°, 80° и 110°, то четвёртый угол равен 130°. 2) Через любые три различные точки плоскости можно провести не менее одной окружности. 3) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную данной.
55)Два каменщика укладывают плиткой два одинаковых участка мостовой, каждый площадью 336 2 м . Первый каменщик в день укладывает на 3 2 м плитки больше, чем второй, и выполняет всю работу на 2 дня быстрее. Сколько квадратных метров плитки укладывает в день первый каменщик? Запишите решение и ответ.
56)Паша написал пять натуральных (необязательно различных) чисел, а потом Лена вычислила все возможные попарные суммы этих чисел. Получилось всего три различных значения: 43, 54 и 65. Посмотрев на полученные Леной значения, Петя смог точно назвать наибольшее из написанных Пашей чисел. Какое это число? Запишите решение и ответ.
57)На кружок по черчению записались семиклассники и восьмиклассники, всего 36 человек. Количество семиклассников, записавшихся на кружок, относится к количеству восьмиклассников как 5:4 соответственно. Сколько восьмиклассников записалось на кружок по черчению?
58)Напишите уравнение прямой, которая проходит через точку 5;19 и параллельна прямой y= 3x .
59)В кулинарии используются меры: стакан, столовая ложка, чайная ложка. В таблице указана соответствующая данной мере масса продукта. Для приготовления одной порции каши нужно взять 1 стакан молока, 3 столовые ложки овсяных хлопьев, 1 столовую ложку сахара, 1/4 чайной ложки соли. Приготовленную кашу нужно заправить сливочным маслом из расчёта 1 чайная ложка на порцию. Найдите общую массу молока, которое потребуется для приготовления 65 порций каши. Ответ дайте в килограммах.
60)Бак автомобиля вмещает 80 л бензина. Перед поездкой бак был заполнен бензином на три четверти. За время поездки было израсходовано 35% бензина. Сколько литров бензина нужно долить, чтобы бак стал полным?
61)Выберите верное утверждение и запишите в ответе его номер. 1) Основания трапеции параллельны. 2) Любые три различные прямые проходят через одну общую точку. 3) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
62)Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 1 км/ч. Ответ дайте в км/ч. Запишите решение и ответ.
63)11 апреля на запись в первый класс независимо друг от друга пришли два будущих первоклассника. Считая, что приходы мальчика или девочки равновероятны, найдите вероятность того, что оба пришедших будущих первоклассника оказались девочками.
64)Стоимость проезда в электричке составляет 120 рублей. Школьникам предоставляется скидка 50%. Сколько рублей будет стоить билет на электричку для школьника после подорожания проезда на 15%?
65)Выберите неверное утверждение и запишите в ответе его номер. 1) Длина каждой стороны треугольника меньше разности длин двух других его сторон. 2) Центром окружности, вписанной в правильный треугольник, является точка пересечения его высот. 3) Если при пересечении двух данных прямых третьей соответственные углы равны, то данные две прямые параллельны.
66)В параллелограмме ABCD биссектриса угла А, равного 60 , ° пересекает сторону ВС в точке М. Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если АB = 5.
67)Двое рабочих одновременно начали выполнять два одинаковых заказа, состоящих из одинакового количества деталей. Первый рабочий выполнял весь заказ равномерно, изготавливая определённое число деталей в день. Второй сначала изготавливал на 6 деталей в день меньше, чем делал первый рабочий, а когда выполнил половину заказа, то стал делать по 56 деталей в день, в результате чего закончил работу одновременно с первым. Какое количество деталей в день делал первый рабочий, если известно, что оно больше 40?
68)На кружок по географии записались шестиклассники, семиклассники и восьмиклассники, всего 31 человек. Среди записавшихся на кружок 9 шестиклассников, а количество семиклассников относится к количеству восьмиклассников как 7:4 соответственно. Сколько семиклассников записалось на кружок по географии?
69)Вероятность того, что в случайный момент времени атмосферное давление в некотором городе не ниже 752 мм рт. ст., равна 0,74. Найдите вероятность того, что в случайный момент времени давление составляет менее 752 мм рт. ст.
70)Стоимость проезда в электричке составляет 150 рублей. Студентам предоставляется скидка 40%. Сколько рублей будет стоить билет на электричку для студента после подорожания проезда на 10%?
71)Выберите верные утверждения и запишите в ответе их номера. 1) Через любые три различные точки плоскости можно провести не более одной окружности. 2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный. 3) Основания любой трапеции параллельны.
72)Путь длиной 39 км первый велосипедист проезжает на 24 минуты дольше второго. Найдите скорость второго велосипедиста, если известно, что она на 2 км/ч больше скорости первого. Ответ дайте в км/ч.
73)В чемпионате мира по футболу участвуют 32 команды. С помощью жребия их делят на восемь групп, по четыре команды в каждой. Группы называют латинскими буквами от A до H. Какова вероятность того, что команда Аргентины, участвующая в чемпионате, окажется в группе A?
74)Натуральное число сначала увеличили на 30%, а потом результат уменьшили на 35%, получилось число 2704. Найдите исходное натуральное число.
75)Выберите верное утверждение и запишите в ответе его номер. 1) Сумма углов выпуклого четырёхугольника равна 180°. 2) Существует точка плоскости, через которую можно провести прямую. 3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
76)Первый рабочий за час делает на 8 деталей больше, чем второй, и выполняет заказ, состоящий из 96 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
77)На доске написано 18 различных целых чисел. Каждое число возвели либо в квадрат, либо в куб и результат записали вместо первоначального числа. Какое наименьшее количество различных чисел могло оказаться записано на доске?
78)Пассажирский поезд, двигаясь со скоростью 36 км/ч, полностью проезжает туннель за 60 секунд. Сколько метров составляет длина этого туннеля, если длина поезда 500 метров? Запишите решение и ответ.
79)На доске написано 75 различных целых чисел. Каждое число возвели либо в квадрат, либо в куб и результат записали вместо первоначального числа. Какое наименьшее количество различных чисел могло оказаться записано на доске? Запишите решение и ответ.
80)Из пункта А в пункт В, расстояние между которыми равно 208 км, вышел катер. Дойдя до пункта В, он вернулся в пункт отправления, затратив на обратный путь на 5 часов меньше. Найдите собственную скорость катера, если скорость течения реки равна 5 км/ч. Ответ дайте в км/ч.
81)Дети водят хоровод вокруг новогодней ёлки. Все девочки нарядились принцессами, а все мальчики — мушкетёрами. Рядом с каждой принцессой обязательно есть хотя бы один мушкетёр. Какое наименьшее число мушкетёров может быть в хороводе, если всего детей 19? Свой ответ обоснуйте.
82)Из А в В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 51 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 34 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
83)Футбольная команда «Черёмушки» по очереди проводит товарищеские матчи с командами «Коньково» и «Ясенево». В начале каждого матча судья бросает монетку, чтобы определить, какая из команд начнёт игру, то есть будет первая владеть мячом. Какова вероятность того, что команда «Черёмушки» по жребию не будет начинать ни один из матчей?
84)Стоимость билетов на поезда дальнего следования одного направления зависит от нескольких факторов и меняется в течение года. В периоды, когда спрос наибольший, цены выше, при понижении спроса в определенные месяцы железнодорожные билеты стоят дешевле. Изменение цен по сравнению с базовым тарифом определяется с помощью сезонных коэффициентов. Например, если обычная цена билета 1000 рублей, но действует коэффициент 1,1, то билет будет стоить на 10% дороже, то есть 1100 рублей. А если действует коэффициент 0,9, то билет будет стоить 900 рублей. На графике показаны цены на железнодорожные билеты в купейные вагоны в разные периоды 2019 года. На сколько рублей выросла цена билетов в купейные вагоны 11 июня по сравнению со второй половиной мая? Чем, по вашему мнению, можно объяснить повышенный спрос на билеты во второй половине лета? Напишите несколько предложений, в которых обоснуйте своё мнение по этому вопросу.
85)Углы треугольника относятся как 3 : 6 : 11. Найдите меньший из этих углов. Ответ дайте в градусах.
86)В магазине продаются цветные карандаши в наборах двух видов — по 10 и по 12 карандашей. В магазине всего 22 набора, а карандашей в них 250. Сколько наборов по 10 карандашей есть в магазине? Запишите решение и ответ.
87)Моторная лодка прошла против течения реки 234 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч. Запишите решение и ответ
88)Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 72 га и распределена между зерновыми и зернобобовыми культурами в отношении 7:2 соответственно. Сколько гектаров занимают зернобобовые культуры?
Ответ: 16.
89)Флакон шампуня стоит 170 рублей. Какое наибольшее число флаконов можно купить на 1100 рублей во время распродажи, когда скидка составляет 35%?
Ответ: 9
90)Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет кефира стоит в магазине 40 рублей. Пенсионер заплатил за пакет кефира 38 рублей. Сколько процентов составляет скидка для пенсионеров?
Ответ: 5
91)В школе 124 учеников изучало французский язык, что составляет 25% от числа всех учеников. Сколько учеников учится в школе?
Ответ: 496
92)Городской бюджет составляет 27 млн рублей, а расходы на одну из его статей составили 10%. Сколько рублей потрачено на эту статью бюджета?
Ответ: 2700000
93)В выборах участвовали два кандидата. Голоса избирателей распределились между ними в отношении 3:2. Сколько процентов голосов получил проигравший?
Ответ: 40
94)На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 189 человек. Голоса между кандидатами распределились в отношении 2:7. Сколько голосов получил победитель?
Ответ: 147
95)Магазин делает пенсионерам скидку. Десяток яиц стоит в магазине 40 рублей, а пенсионер заплатил за них 35 рублей 60 копеек. Сколько процентов составила скидка для пенсионера?
Ответ: 11
96)В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 15 % от стоимости купленной мебели. Шкаф стоит 3000 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
Ответ: 3450
97)Ежемесячная плата за телефон составляет 300 рублей в месяц. В следующем году она увеличится на 6%. Сколько рублей будет составлять ежемесячная плата за телефон в следующем году?
Ответ: 318
98)Магазин делает пенсионерам скидку. Батон хлеба стоит в магазине 20 рублей, а пенсионер заплатил за него 19 рублей 40 копеек. Сколько процентов составила скидка для пенсионера?
Ответ: 3
99)Число хвойных деревьев в парке относится к числу лиственных как 7:13 соответственно. Сколько процентов деревьев в парке составляют хвойные?
Ответ: 45
100)В цветнике растут только тюльпаны, гиацинты и пионы. Их количества относятся как 2 : 6 : 8 соответственно. Всего в цветнике 64 растения. Сколько пионов растет в цветнике.
Ответ: 32
101)На фестивале выступают группы — по одной от каждой из заявленных стран, среди этих стран Румыния, Болгария и Греция. Порядок выступления определяется жребием. Какова вероятность того, что группа из Румынии будет выступать до группы из Болгарии, но после группы из Греции?
Ответ: 1/6
102)На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.
Ответ: 0,88
103)Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
Ответ: 0,2
104)Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.
Ответ: 0,85
105)На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Ответ: 0,25
106)В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Ответ: 0,2
107)В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
Ответ: 0,9
108)Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.
Ответ: 0,5
109)Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
Ответ: 0,18
110)В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
Ответ: 0,9
111)В театральной студии 35 учеников, среди них 9 человек изучают ораторское искусство, а 12 — актерское мастерство. При этом нет никого, кто бы занимался и тем, и другим. Найдите вероятность того, что случайно выбранный ученик театральной студии занимается ораторским искусством или актерским мастерством.
Ответ: 0,6
112)В среднем из 40 карманных фонариков, поступивших в продажу, шесть неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Ответ: 0,85
113)В среднем из 50 карманных фонариков, поступивших в продажу, семь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Ответ: 0,86
114)В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку.
Ответ: 0,56
115)Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.
Ответ: 0,5
116)В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Ответ: 0,3
117)Из 1600 пакетов молока в среднем 80 протекают. Какова вероятность того, что случайно выбранный пакет молока не течёт?
Ответ: 0,95
118)Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Ответ: 0,5
119)Из каждых 1000 электрических лампочек 5 бракованных. Какова вероятность купить исправную лампочку?
Ответ: 0,995
120)В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Ответ: 0,45
121)Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.
Ответ: 0,25
122)У Алисы в копилке лежат монеты по 2 рубля и по 5 рублей. Если все двухрублевые монеты, которые лежат в копилке, сложить в стопки по 11 монет, то получится три полных стопки, а четвёртая неполная. Если же сложить пятирублёвые монеты в стопки по 3 монеты, то получится четыре полных стопки, а пятая неполная. Сколько всего рублей у Алисы в копилке, если двухрублёвые монеты составляют такую же сумму (в рублях), что и пятирублёвые?
Ответ: 140
123)Паша выписал на доску пять натуральных (не обязательно различных) чисел и вычислил всевозможные попарные суммы этих чисел. Получилось всего три различных значения: 63, 56 и 49. Чему равно наибольшее из написанных на доске чисел?
Ответ: 35
124)Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 0 до 10 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма — это среднее арифметическое всех оценок экспертов. По новойсистеме оценивания рейтинг кинофильма оценивают следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое оставшихся оценок. Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.
Ответ: 4/7
125)Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11. Приведите все примеры задуманных чисел, для которых на доске будет записан набор 9, 10, 11, 19, 20, 21, 22, 30, 31, 32, 33, 41, 42, 43, 52.
Ответ: 9, 10, 11, 11, 11
126)У Лены три набора, в каждом из которых одинаковое количество ручек (больше 1). У Юли несколько (больше 1) наборов ручек, по 5 штук в каждом. Можно ли разложить все ручки Юли и Лены в k наборов по k ручек в каждом (k > 3)?
Ответ: да
127)Известно, что в кошельке лежало n монет, каждая из которых могла иметь достоинство 2, 5 или 10 рублей. Лена сделала все свои покупки, расплатившись за каждую покупку отдельно без сдачи только этими монетами, потратив при этом все монеты из кошелька. Какое наименьшее количество пятирублёвых монет могло быть в кошельке, если Лена купила только альбом за 96 рублей и n = 19?
Ответ: 6
128)Красный карандаш стоит 18 рублей, синий — 14 рублей. Нужно купить карандаши, имея всего 495 рублей и соблюдая дополнительное условие: число синих карандашей не должно отличаться от числа красных карандашей больше чем на пять. Какое наибольшее число карандашей можно купить при таких условиях?
Ответ: 31
129)На станцию привезли некоторое количество контейнеров. В каждом контейнере находилось одно и то же число телевизоров (большее 1). Телевизоры перегрузили в вагоны. Получилось 12 полных вагонов и еще один вагон, в котором всего 5 телевизоров. Через несколько дней привезли такие же контейнеры. Телевизоры снова перегрузили в вагоны. На этот раз получилось 5 вагонов, причем в последнем до полного вагона не хватало одного телевизора. Сколько телевизоров вмещает один контейнер?
Ответ: 37
130)Мастер делает за один час целое число деталей, большее 18, а ученик — на 10 деталей меньше. Мастер выполняет заказ за целое число часов, а три ученика вместе — на два часа быстрее. Из какого числа деталей состоит заказ?
Ответ: 120
131)В турнире по шахматам принимают участие мальчики и девочки. За победу в шахматной партии начисляют 1 очко, за ничью — 0,5 очка, за проигрыш — 0 очков. По правилам турнира каждый участник играет с каждым другим дважды. Сколько девочек могло принимать участие в турнире, если известно, что их в 9 раз меньше, чем мальчиков, и что мальчики набрали в сумме ровно в четыре раза больше очков, чем девочки?
Ответ: 1 девочка
132)На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18. Каких чисел написано больше: положительных или отрицательных?
133)На складе находятся музыкальные центры двух типов. Музыкальный центр первого типа весит 15 кг, второго типа — 18 кг. Музыкальный центр первого типа стоит 6000 рублей, музыкальный центр второго типа — 8000 рублей. Общий вес музыкальных центров равен 279 кг. Найдите минимальную и максимальную возможные суммарные стоимости находящихся на складе музыкальных центров в рублях.
Ответ: 122000 рублей
134)Если построить солдат по 15 человек в шеренге, то последняя шеренга окажется неполной. Если же построить их по 14 человек в шеренге, то все шеренги окажутся полными, но их число будет больше на 1. Если же построить тех же солдат в шеренги по 9 в каждой, то последняя шеренга опять будет неполной, а число шеренг увеличится еще на 9. Сколько всего солдат?
Ответ: 224
135)Назовем натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично (совпадают первая и последняя цифра,вторая и предпоследняя, и т. д.). Например числа 121 и 953 359 являются палиндромами, а числа 10 и 953 953 не являются палиндромами. Найдите 37−е по порядку число-палиндром, которое делится на 15.
Видео:Разбор ВПР 8 класс по математике. Вебинар | МатематикаСкачать

ВПР по математике 8 класс 2021 Варианты с ответами
В период с 15 марта по 21 мая 2021 года состоялись всероссийские проверочные работы по математике в 8 классах.
После проведения ВПР в школах стали доступны реальные варианты и критерии оценки.
Для каждой школы варианты формировались индивидуально из банка заданий ВПР.
ВПР 2021 по математике для 8 класса с ответами
| Комплект ВПР 1 | |
| Вариант 1 | Скачать ответы |
| Вариант 2 | Скачать ответы |
| Комплект ВПР 2 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект ВПР 3 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект ВПР 4 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект ВПР 5 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект ВПР 6 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект ВПР 7 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект ВПР 8 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект ВПР 9 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект ВПР 10 | |
| variant 1 | otvet |
| variant 2 | otvet |
Типы заданий, сценарии выполнения заданий ВПР 2021 по математике 8 класс
В задании 1 проверяется владение понятиями «отрицательное число», «обыкновенная дробь», «десятичная дробь», вычислительными навыками.
В задании 2 проверяется умение решать линейные, квадратные уравнения, а также системы уравнений.
В задании 3 проверяется умение решать задачи на части.
В задании 4 проверяется знание свойств целых чисел и правил арифметических действий.
Задание 5 проверяет владение понятиями «функция», «график функции», «способы задания функции».
Задание 6 направлено на проверку умения извлекать и анализировать информацию, представленную в таблицах, на диаграммах, графиках.
В задании 7 проверяются умения читать информацию, представленную в таблицах, на диаграммах, графиках и определять статистические характеристики данных.
В задании 8 проверяется умение сравнивать действительные числа.
В задании 9 проверяется умение выполнять преобразования буквенных дробно-рациональных выражений.
Задание 10 направлено на проверку умения в простейших случаях оценивать вероятность события.
Задание 11 проверяет умение решать текстовые задачи на проценты, в том числе задачи в несколько действий.
Задания 12–15 и 17 проверяют умение оперировать свойствами геометрических фигур, а также знание геометрических фактов и умение применять их при решении практических задач.
В задании 16 проверяются умения извлекать из текста необходимую информацию, представлять данные в виде диаграмм, графиков.
Задание 18 направлено на проверку умения решать текстовые задачи на производительность, движение.
Задание 19 является заданием высокого уровня сложности и направлено на проверку логического мышления, умения проводить математические рассуждения.
🌟 Видео
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Разбор ВПР по математике 8 класс | Задачи, в которых ошибаются все | Средняя школа | УмскулСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

ВПР 8 класс математикаСкачать

Разбор ВПР по математике. 8 класс. Вебинар | МатематикаСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

ВПР 8 КЛАСС ЗАДАНИЕ 13 #математика #2023 #огэ #mathematicsСкачать

8 класс. ВПР-2022 по МАТЕМАТИКЕ . Часть 1Скачать

Впр-2023. Математика, 8 класс. Задание №5. Формула линейной функцииСкачать

Разбор варианта ВПР 8 класс 2022Скачать

УРАВНЕНИЕ ЛИНЕЙНОЙ ФУНКЦИИ. ВПР. 7 - 8 КЛАСС.Скачать

ВПР 2023 // Математика 8 класс // Типовой вариант // Решение, ответы, баллы // Сборник ЛысенкоСкачать

Разбор демо-версии ВПР 2022 по математике. 8 класс.Скачать

Вся алгебра 8 класса в одном задании | МатематикаСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

ВПР-2023. Математика, 8 класс. Задание №1Скачать

ВПР по математике 8 класс. На троечкуСкачать