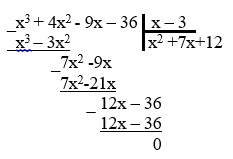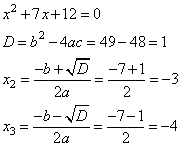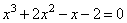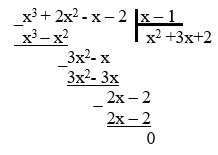- Решение уравнений
- Разбор типовых вариантов задания №21 ОГЭ по математике
- Демонстрационный вариант ОГЭ 2019
- Первый вариант задания
- Второй вариант задания
- Решение кубических уравнений
- Решение двучленного кубического уравнения вида A x 3 + B = 0
- Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
- Решение кубических уравнений с рациональными корнями
- Решение кубических уравнений по формуле Кардано
- Алгебраические уравнения и способы их решения. Уравнения третьей и четвертой степени
- 🎥 Видео
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение уравнений
В данном задании необходимо решить уравнение степени больше двух — это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий!
Разбор типовых вариантов задания №21 ОГЭ по математике
Демонстрационный вариант ОГЭ 2019
Алгоритм решения:
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
Решение:
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x 4 — (4x — 5) 2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х 2 – (4х-5))( х 2 + (4х-5)) = 0, или (х 2 – 4х+5)(х 2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х 2 – 4х+5 = 0 и х 2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b 2 -4ac = 16-20 = — 4, это означает, что первое уравнение х 2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
Определим корни второго уравнения:
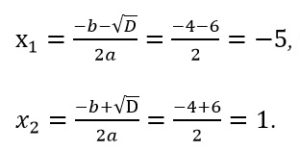
Первый вариант задания
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
Решение:
1. Перед нами уравнение третьей степени общего типа.
2. Найдем делители свободного члена данного уравнения. Это числа: 1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12;.18; -18; 36; -36.
3. Рассмотрим числа 1; -1; 2; -2; 3; -3. Это наименьшие среди найденных делителей. Подставим их по очереди в уравнение вместо х:
- для x=1:
— не подходит;
- для x=-1:
— не подходит;
- для х=2: 2 3 +4∙2 2 -9∙2=8=16-18-36=-38≠0 — не подходит;
- для х=-2: (-2) 3 +4∙(-2) 2 -9∙(-2)-36=-8+16+18-36=-10≠0 – не подходит;
- для x=3:
— подходит.
Мы нашли один корень.
4. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
| 1 | 4 | -9 | -36 | |
| 3 | 1 | 7 | 12 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
5. После деления получаем квадратный трехчлен:
Составим квадратное уравнение для вычисления оставшихся двух корней:
6. Решим его с помощью формул корней и дискриминанта
7. Получили три корня 3; -3; -4.
Второй вариант задания
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: 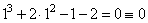
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
5. Получаем квадратный трехчлен
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Решение кубических уравнений
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Видео:ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Видео:ВСЕ ТИПЫ 20 ЗАДАНИЕ 2 ЧАСТЬ ОГЭ МАТЕМАТИКА 2023Скачать

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Видео:Задание №20. Уравнение 2 часть ОГЭ по математике 2023 | УмскулСкачать

Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Видео:Задание 20 ОГЭ математика 2024 2 часть. Кубические уравненияСкачать

Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгебраические уравнения и способы их решения. Уравнения третьей и четвертой степени
Что делать, если вам – например, на Профильном ЕГЭ по математике – встретилось не квадратное уравнение, а кубическое? Или даже уравнение четвертой степени? Ведь для уравнений третьей, четвертой и более высоких степеней нет таких простых формул, как для квадратного уравнения.
В этой статье – способы решения сложных алгебраических уравнений. Замена переменной, использование симметрии и даже деление многочлена на многочлен.
Вспомним основные понятия.
Корень уравнения – такое число, которое мы можем подставить вместо переменной в уравнение и получить истинное равенство.
Например, число 3 – корень уравнения 2x = 6.
Решить уравнение – значит найти его корни или доказать, что их нет.
Равносильными называются уравнения, множества решений которых совпадают. Другими словами, у них одни и те же корни.
Например, уравнения и равносильны. Их корни совпадают: или
Замена переменной – ключ к решению многих задач.
Если приводить обе части к одному знаменателю, получим уравнение четвертой степени. Вряд ли мы с ним справимся.
Сделаем замену Тогда
С новой переменной уравнение стало проще:
Умножим обе части на 10t. Получим квадратное уравнение:
Корни этого уравнения: или
Вернемся к переменной
Дискриминант этого уравнения отрицателен, корней нет.
Если , то Получим квадратное уравнение для :
У этого уравнения два корня: или Это ответ.
Не будем спешить раскрывать скобки. Ведь раскрыв их, мы получили бы уравнение четвертной степени.
Посмотрим на уравнение внимательно.
На координатной прямой точки 1; 3; –5; –7 расположены симметрично относительно точки
Сделаем замену , тогда .
Мы выразили все «скобки», то есть все множители, через новую переменную. Вот что это дает:
И еще одна замена: .
Обычное квадратное уравнение. Замечательно!
Подберем его корни по теореме Виета. Заметим, что
Если , то нет решений.
Если , то Тогда или
Дальше – еще интереснее.
3. Решите уравнение
Сделаем замену . То, что в правой части в скобках, заменили на новую переменную.
Получили квадратное уравнение:
Следующее уравнение решим с помощью группировки слагаемых.
4. Решите уравнение
Разложим левую часть уравнения на множители. Сгруппируем слагаемые:
Первые два слагаемых – сумма кубов. Применим формулу: . Получим:
Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Записывается это так:
У нас появилось новое обозначение: — знак совокупности.
Такой знак означает «или».
Запись читается как « или или ».
Решая уравнения и особенно неравенства, мы будем постоянно пользоваться знаками системы и совокупности. Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.
5. Решите уравнение
Разложить левую часть на множители с первой попытки не удается.
Оказывается, если уравнение третьей (четвертой, пятой…) степени имеет целые корни, то находятся они среди делителей свободного члена (слагаемого, не содержащего x). В данном случае – среди целых делителей числа 24.
Выпишем целые делители числа 24:
1; –1; 2; –2; 3; –3; 4; –4; 6; –6; 8; –8; 12; –12; 24; –24
Подставляя их по очереди в уравнение, при получаем верное равенство:
Это значит, что левую часть уравнения можно разложить на множители:
Чтобы найти , поделим выражение на . В столбик. Так же, как мы делим друг на друга числа.
Немного непривычно, да? Потренируйтесь – у вас получится!
6. Решите уравнение
А если сделать замену ?
Получаем квадратное уравнение: . Удачная замена!
Если , то 
7. Решите уравнение
Разложить на множители? Но как? И замена не видна сразу. Посмотрим на уравнение внимательно. Его коэффициенты: 1, — 5, 4, — 5, 1.
Такое уравнение называется симметрическим.
Разделим обе его части на . Мы можем это сделать, поскольку не является корнем нашего уравнения.
🎥 Видео
ОГЭ. Задание 21. Уравнение третей степени. Разложение на множители.Скачать

Математика| СтепениСкачать

Все типы 8 задания ОГЭ 2022 | Свойства корнейСкачать

ОГЭ №21 Как решать уравнение (x-3)^4-3(x-3)^2-10=0 Уравнение 4 степени Уравнение с одинаковыми скобкСкачать

Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Все типы задания 6 | Математика ОГЭ 2023 | УмскулСкачать

Возвратные уравнения 3 степениСкачать

Огэ математика. Решение уравнений третьей степени. Кубические уравнения. Группировка. Вторая частьСкачать

ОГЭ ДЛЯ НОЛИКОВ. СТЕПЕНИ, ЗАДАНИЕ-8Скачать

Решение уравнения третьей степени x³-9x-12=0Скачать

Все типы 20 задания ОГЭ по математике | Молодой репетиторСкачать

ОГЭ задача 21 (системы уравнений) #3Скачать

Разбор всех типов задания №6 из ОГЭ по математике 2024Скачать

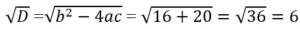
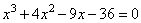
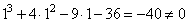 — не подходит;
— не подходит;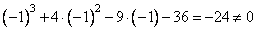 — не подходит;
— не подходит;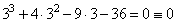 — подходит.
— подходит.