ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ — колебания, происходящие под действием внешней переменной силы (вынуждающей силы).
Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.
Рассмотрим вынужденные колебания на примере реального (с трением) пружинного маятника. Будем отталкиваться от уравнения движения (второй закон Ньютона) , которое мы написали для затухающих колебаний. При наличии дополнительной вынуждающей силы F(t) необходимо дописать ее в правую часть уравнения. В каноническом виде дифференциальное уравнение вынужденных механических колебаний имеет вид:
Для пружинного маятника:

Для того, чтобы возникли периодические колебания, вынуждающая сила сама должна быть периодической. Пусть 


Общее решение этого неоднородного дифференциального уравнения представляет собой, как известно из теории дифференциальных уравнений, сумму общего решения однородного уравнения и любого частного решения неоднородного. Общее решение однородного уравнения нам известно, это — уравнение затухающих колебаний. Оно нас не интересует, так как при 
где А — амплитуда вынужденных колебаний, j ۪ — сдвиг фаз между смещением и приложенной силой.
Получившиеся колебания подчиняются закону синуса (или косинуса), то есть являются синусоидальными или гармоническими. Но это не свободные колебания в системе без трения; здесь вынуждающая сила постоянно поставляет энергию в систему, в точности компенсирующую потери на преодоление сил трения.
Необходимо теперь найти амплитуду вынужденных колебаний и сдвиг фаз. Для этого необходимо подставить выражение для х в дифференциальное уравнение вынужденных колебаний. Обратите внимание, что необходимо найти два неизвестных из одного уравнения. Это возможно, если в процессе вычислений воспользоваться дополнительным (очевидным в процессе выкладок) условием. Попытайтесь проделать это.
Для амплитуды и сдвига фаз получаются следующие выражения:

здесь w0 — частота свободных (незатухающих) колебаний маятника; b — коэффициент затухания.
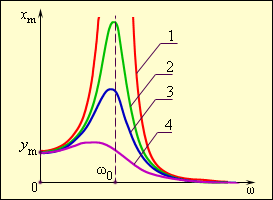
Обратите внимание, что амплитуда вынужденных колебаний зависит от соотношения частоты вынуждающей силы и собственной частоты маятника. Максимальное значение амплитуды получается, если
Частота 
Помимо поведения амплитуды при резонансной частоте рассмотрим ещё два предельных случая: 
В первом мы получим обычное статическое смещение маятника под действием постоянной силы F0 (статическое растяжение пружины):
Во втором случае амплитуда равна нулю: инерция маятника не может успевать реагировать на бесконечную частоту.
Зависимость сдвига фаз от соотношения частот представлена на рисунке. Сдвиг фаз между смещением и вынуждающей силой обусловлен инерцией маятника.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Уравнений вторым законом ньютона для вынужденных колебаний является
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными .
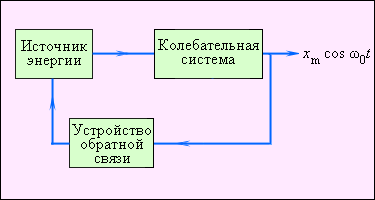
В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой , воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте .
Если свободные колебания происходят на частоте , которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте внешней силы .
После начала воздействия внешней силы на колебательную систему необходимо некоторое время для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания свободных колебаний в колебательной системе.
В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте и свободные колебания на собственной частоте . Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте внешней вынуждающей силы.
Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила 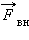
| m cos . |
где m – амплитуда колебаний, – круговая частота.
Такой закон перемещения можно обеспечить с помощью шатунного механизма, преобразующего движение по окружности в поступательно-возвратное движение (рис. 2.5.1).
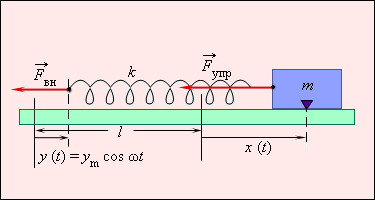 | ||||||||||||
| Рисунок 2.5.1. Если левый конец пружины смещен на расстояние , а правый – на расстояние от их первоначального положения, когда пружина была недеформирована, то удлинение пружины равно:
Второй закон Ньютона для тела массой принимает вид :
В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой . Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой:
где
Уравнение (**) не учитывает действия сил трения. В отличие от уравнения свободных колебаний (*) (см. §2.2) уравнение вынужденных колебаний (**) содержит две частоты – частоту свободных колебаний и частоту вынуждающей силы. Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону
Амплитуда вынужденных колебаний m и начальная фаза зависят от соотношения частот и и от амплитуды ym внешней силы. На очень низких частотах, когда , движение тела массой , прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом , и пружина остается практически недеформированной. Внешняя сила Если частота внешней силы приближается к собственной частоте , возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом . Зависимость амплитуды m вынужденных колебаний от частоты вынуждающей силы называется резонансной характеристикой или резонансной кривой (рис. 2.5.2). При резонансе амплитуда m колебания груза может во много раз превосходить амплитуду m колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе. У колебательных систем с не очень высокой добротностью () резонансная частота несколько смещается в сторону низких частот. Это хорошо заметно на рис. 2.5.2. Явление резонанса может явиться причиной разрушения мостов, зданий и других сооружений, если собственные частоты их колебаний совпадут с частотой периодически действующей силы, возникшей, например, из-за вращения несбалансированного мотора.
|








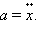 Тогда уравнение вынужденных колебаний запишется в виде
Тогда уравнение вынужденных колебаний запишется в виде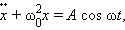
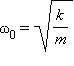 – собственная круговая частота свободных колебаний, – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина определяется выражением:
– собственная круговая частота свободных колебаний, – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина определяется выражением: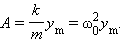
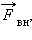 приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при стремится к нулю.
приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при стремится к нулю.