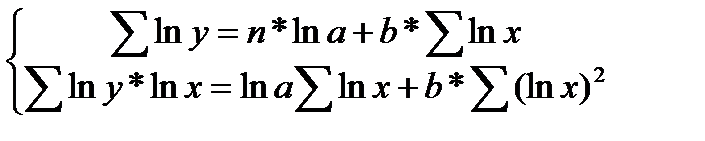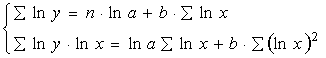Уравнением нелинейной регрессии являющейся нелинейной по параметрам (6 видео)

Уравнение нелинейной регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

Содержание

Виды нелинейной регрессии
Эконометрика
Тема 4. Множественная регрессия.
Вопросы
1. Нелинейная регрессия. Нелинейные модели и их линеаризация.
Нелинейная регрессия
Виды нелинейных регрессионных моделей, расчет их параметров
📹 Видео

Видео:Эконометрика. Нелинейная регрессия. Гипербола.Скачать

Виды нелинейной регрессии

Вид	Класс нелинейных моделей
Полиномальное уравнение регрессии: y = a + bx + cx 2 (см. метод выравнивания) Гиперболическое уравнение регрессии: Квадратичное уравнение регрессии:	Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам
Показательное уравнение регрессии: Экспоненциальное уравнение регрессии: Степенное уравнение регрессии: Полулогарифмическое уравнение регрессии: y = a + b lg(x)	Нелинейные по оцениваемым параметрам

Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.

Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.

Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .

Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .

Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):

Замена переменных.
Логарифмирование обеих частей уравнения.
Комбинированный.

y = f(x)	Преобразование	Метод линеаризации
y = b x a	Y = ln(y); X = ln(x)	Логарифмирование
y = b e ax	Y = ln(y); X = x	Комбинированный
y = 1/(ax+b)	Y = 1/y; X = x	Замена переменных
y = x/(ax+b)	Y = x/y; X = x	Замена переменных. Пример
y = aln(x)+b	Y = y; X = ln(x)	Комбинированный
y = a + bx + cx 2	x₁ = x; x₂ = x 2	Замена переменных
y = a + bx + cx 2 + dx 3	x₁ = x; x₂ = x 2 ; x₃ = x 3	Замена переменных
y = a + b/x	x₁ = 1/x	Замена переменных
y = a + sqrt(x)b	x₁ = sqrt(x)	Замена переменных

Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:

Построить поле корреляции и сформулировать гипотезу о форме связи.
Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
Оценить тесноту связи с помощью показателей корреляции и детерминации.
Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
Оценить с помощью средней ошибки аппроксимации качество уравнений.
Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
Оценить полученные результаты, выводы оформить в аналитической записке.

Год	Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y	Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х
1995	872	515,9
2000	3813	2281,1
2001	5014	3062
2002	6400	3947,2
2003	7708	5170,4
2004	9848	6410,3
2005	12455	8111,9
2006	15284	10196
2007	18928	12602,7
2008	23695	14940,6
2009	25151	16856,9

Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x

Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626

Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706

Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535

Видео:Эконометрика. Нелинейная регрессия: парабола.Скачать

Эконометрика

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ

Кафедра экономико-метематических моделей

Тема 4. Множественная регрессия.

Вопросы

1. Нелинейная регрессия. Нелинейные модели и их линеаризация.

Нелинейная регрессия

При рассмотрении зависимости экономических показателей на основе реальных статистических данных с использованием аппарата теории вероятности и математической статистики можно сделать выводы, что линейные зависимости встречаются не так часто. Линейные зависимости рассматриваются лишь как частный случай для удобства и наглядности рассмотрения протекаемого экономического процесса. Чаще встречаются модели которые отражают экономические процессы в виде нелинейной зависимости.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам: регрессии, нелинейные по оцениваемым параметрам.

Нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам

Данный класс нелинейных регрессий включает уравнения, в которых зависимая переменная линейно связана с параметрами. Примером могут служить:

полиномы разных степеней

(полином k-й степени)

и равносторонняя гипербола

При оценке параметров регрессий нелинейных по объясняющим переменным используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной регрессии. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК).

Полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез.

Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.

Равносторонняя гипербола, для оценки параметров которой используется тот же подход «замены переменных» (1/x заменяют на переменную z) хорошо известна в эконометрике.

Она может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции. Также примером использования равносторонней гиперболы являются кривые Филлипса и Энгеля..

Регрессии нелинейные по оцениваемым параметрам

К данному классу регрессий относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами. Примером таких нелинейных регрессий являются функции:

• степенная — ;

• показательная — ;

• экспоненциальная —

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции и для оценки её параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении спроса от цен: , где у — спрашиваемое количество; х — цена;

Данная модель нелинейна относительно оцениваемых параметров, т. к. включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду . Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой а и b могут быть найдены МНК.

Широкое использование степенной функции связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.

Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b.

По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений ( Х, млн. руб. ).

Видео:Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Виды нелинейных регрессионных моделей, расчет их параметров

Хотя во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат, однако ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Так близость линейного коэффициента корреляции к нулю еще не значит, что связь между соответствующими экономическими переменными отсутствует. При слабой линейной связи может быть очень тесной, например, не линейная связь. Поэтому необходимо рассмотреть и нелинейные регрессии, построение и анализ которых имеют свою специфику.

В случае, когда между экономическими явлениями существует нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных эконометрических моделей.

Различает две группы нелинейных регрессионных моделей:

модели, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

модели нелинейные по оцениваемым параметрам.

К первой группе относятся, например, следующие виды функций:

— полином 2-й степени;

— полином 3-й степени;

— гипербола.

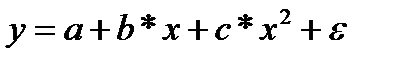
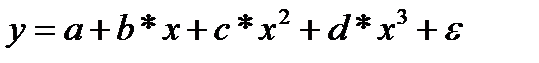
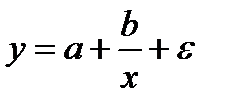
Ко второй группе относятся:

— степенная;

— показательная;

— экспоненциальная

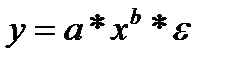
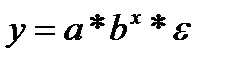
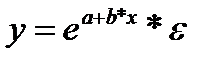
и др. виды функций.

Классическим примером функций, относящихся к первой группе, являются кривые Филипса и Энгеля:

и , соответственно.

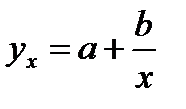
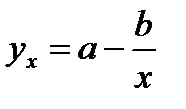
Первая функция характеризует нелинейные соотношения между нормой безработицы x и процентом прироста заработной платы у. Из данной зависимости следует, что с ростом уровня безработицы темпы роста заработной платы в пределе стремится к нулю.

Вторая функция устанавливает закономерность – с ростом дохода доля расходов на продовольствие — уменьшается. Здесь у, обозначает — долю расходов на непродовольственные товары; х – доходы.

Первая группа нелинейных функций легко может быть линеаризована (приведены к линейному виду). Например, для полинома к-го порядка

производя замену:

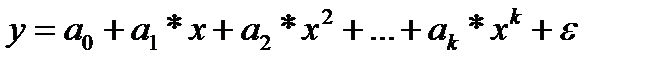
х=х₁, х 2 =х₂, х 3 =х₃,…,х к =х_к получим линейную модель вида

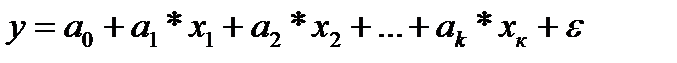
32. Модели регрессии, нелинейные по оцениваемым коэффициентам

Модели регрессии, нелинейные по оцениваемым коэффициентам могут быть линеаризованы путем соответствующих замен.

Для оценки параметров нелинейных функций первой группы можно использовать, обычный МНК, аналогично, как и в случае линейных функций.

Иначе обстоит дело с группой регрессионных, нелинейных функций по оцениваемым параметрам. Данную группу функций можно разбить на две подгруппы:

нелинейные модели внутренне линейные;

нелинейные модели внутренне нелинейные.

Рассмотрим степенную функцию 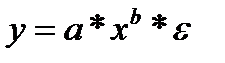. Она нелинейна относительно параметров а и b. Однако ее можно считать внутренне линейной, так как, прологарифмировав ее можно привести к линейному виду:

ln y =ln a+b*ln x +ln ε .

Следовательно, ее параметры могут быть найдены обычным МНК.

Если модель представить в виде:

y = a *x b +ε , то модель становится внутренне нелинейной, т.к. ее невозможно преобразовать в линейный вид.

Внутренне нелинейной будет и модель вида

В эконометрических исследованиях, часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые легко преобразуются в линейный вид, относятся к группе линейных моделей. Например, к линейным относят модель:

y = e a + bx *ε , так как

Если, модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные методы, успешность которых зависит от вида функции и особенностей применяемого итеративного подхода.

МНК в случае нелинейных функций, рассмотрим на примере оценки параметров степенной функции y =a*x b *ε.

Прологарифмировав данную функцию, получим:

ln y =ln a+b *ln x + ln ε или, производя обозначения:

Применив МНК к полученному уравнению:

, или

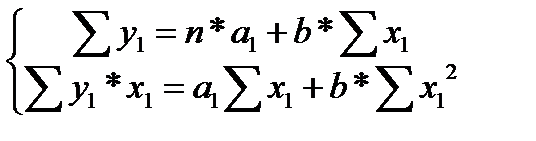
Параметр b определяется непосредственно из системы, а параметр а – косвенным путем: a=e a 1

33. Метод наименьших квадратов для моделей регрессии, нелинейных по факторным переменным

Применение МНК для оценки параметров моделей регрессии, нелинейных по факторным переменным рассмотрим на примере параболы второй степени. При метод МНК видоизменяет первоначальные уравнения и приводит их к следующей системе нормальных уравнений:

(36.1)

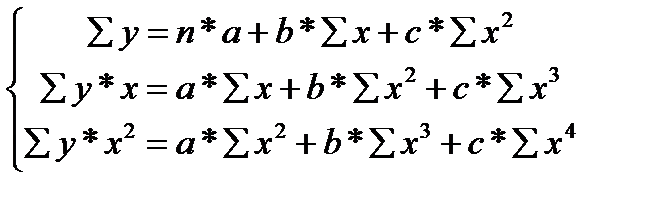
Решить данную систему относительно параметров а, b, с можно методом определителей:

(36.2)

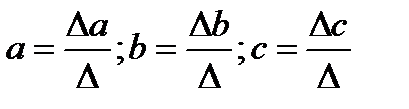
где Δ — определитель системы;

Δа, Δb, Δс — частные определители для каждого из параметров.

При b > О и с 0 имеем обратную зависимость, которая при х → ∞ характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр а.