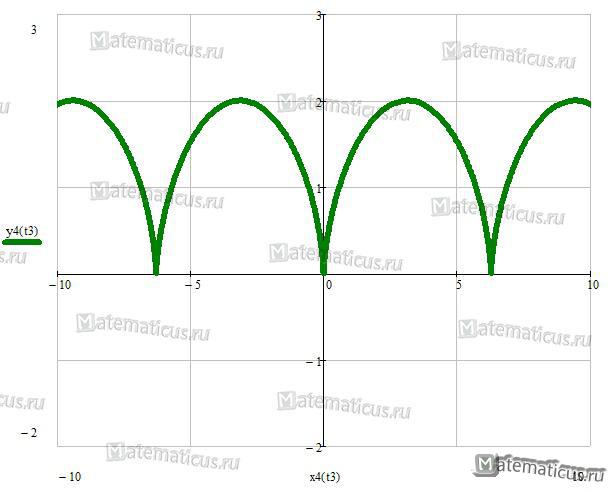
Уравнение звезды в декартовой системе координат (4 видео)

Содержание

Замечательные кривые
Логарифмическая спираль
Кардиоида
Астроида
Строфоида
Декартов лист
Циссоида
Циклоида
Кохлеоида
Уравнения кривых. Астроида.
Уравнение звезды в декартовой системе координат
Полярная система координат
Фигуры в полярных координатах
Окружность
«Пируэты» окружности
Астроида (Astroid)
Эпициклоиды
💥 Видео

Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Замечательные кривые

Семейство роз Гранди

Уравнение имеет вид:

a — радиус лепестка;

k — положительный параметр, отвечает за количество лепестков.

Рисунок 1 — роза с тремя лепестками ρ=sin3φ

Рисунок 2 — роза с 16 лепестками ρ=sin8φ

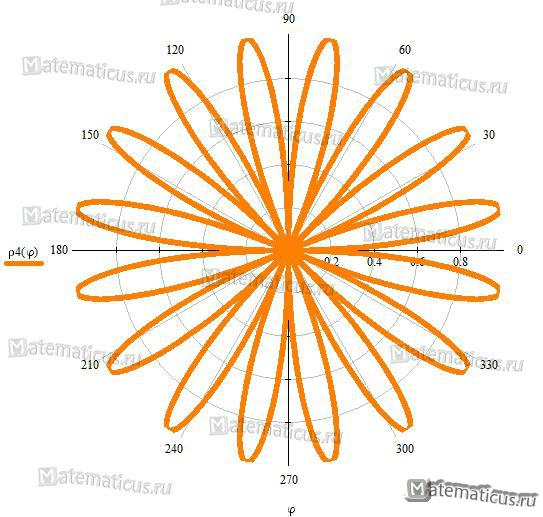
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ

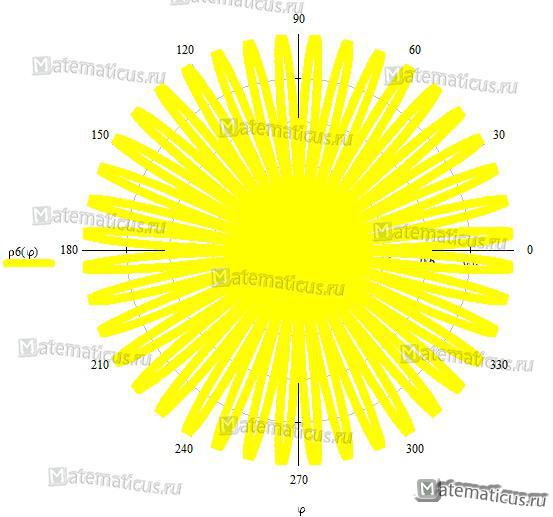
Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ

Видео:Построение кривой в полярной системе координатСкачать

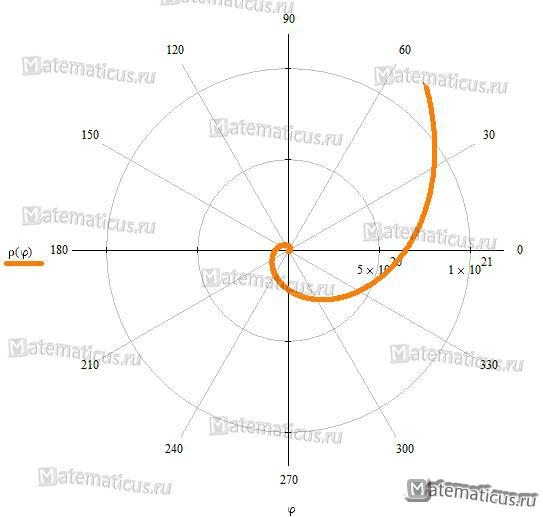
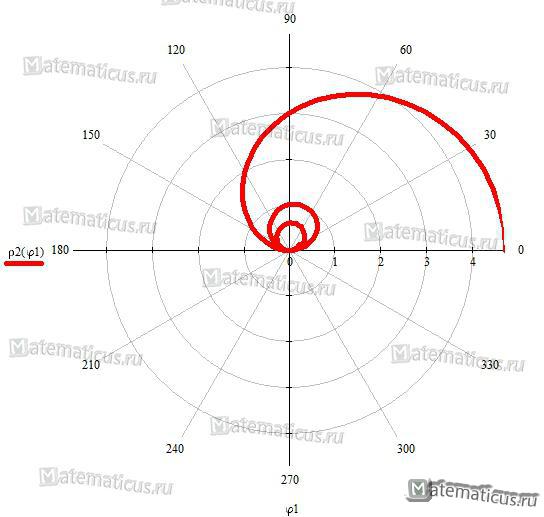
Логарифмическая спираль

Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

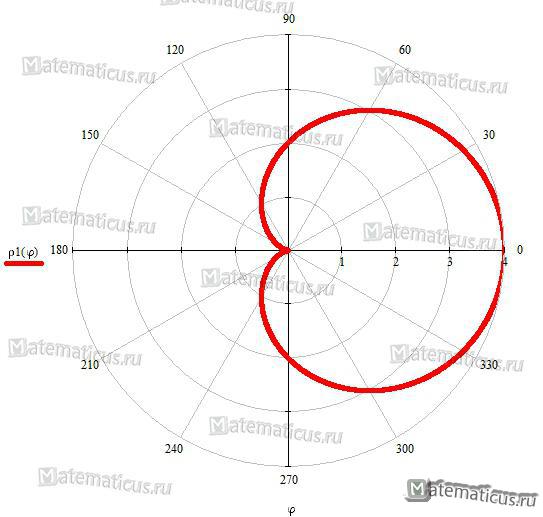
Кардиоида

Уравнение кардиоиды (перев. греч. сердце и вид) в полярных координатах:

Видео:Модель декартовой системы координат.Скачать

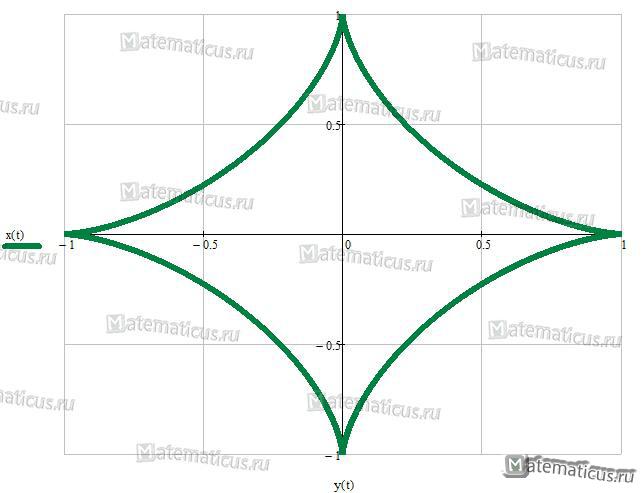
Астроида

Уравнение астроиды (перев. греч. звезда и вид) :

x 2/3 + y 2/3 = a 2/3

Видео:Видеоурок "Преобразование координат"Скачать

Строфоида

Уравнение строфоиды (перев. греч. крученая лента, поворот) :

y 2 (a — x)= x 2 (a + x)

Уравнение строфоиды в полярной системе координат:

Видео:Полярная система координатСкачать

Видео:A.6.6 Переход между декартовой и другими системами координатСкачать

Декартов лист

Уравнение декартова листа :

x 2 + y 2 — 3axy = 0

Уравнение декартова листа в полярной системе координат:

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Циссоида

Уравнение циссоиды Диоклеса (перев. греч. плющ, вид) в прямоугольной системе координат :

Параметрическое уравнение циссоиды:

x = a t 2 /(1 + t 2 )

x = a t 3 /(1 + t 2 )

Уравнение циссоиды в полярной системе координат:

Видео:Видеоурок "Полярная система координат"Скачать

Циклоида

Параметрическое уравнение циклоиды :

Видео:Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Кохлеоида

Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:

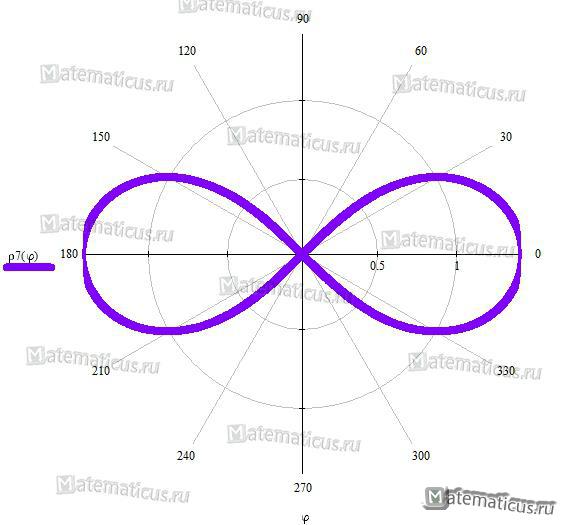
Лемниската Бернулли

Уравнение лемниската Бернулли в прямоугольных координатах:

(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )

Уравнение лемниската Бернулли в полярных координатах:

Архимедова спираль рассмотрена здесь подробно.

Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.

Видео:Сферические координатыСкачать

Уравнения кривых. Астроида.

Астроида – плоская кривая, которую формирует траектория точки, расположенной на окружности радиуса r, катящейся без трения по внутренней стороне неподвижной окружности радиуса R = 4r.

Параметрическое уравнение:

Уравнение в алгебраическом виде:

Длина дуги от точки с 0 до t ≤ π/2:

Длина всей кривой равна 6R.

Радиус кривизны описывается формулой:

Площадь, ограниченная кривой представлена такой формулой:

Объем тела вращения относительно любой координатной оси описан формулой:

Видео:Значение Янтр и Мандал: Влияние и Различия в Магической ПрактикеСкачать

Уравнение звезды в декартовой системе координат

Примеры для статьи — polar.zip

Кроме привычной нам прямоугольной декартовой системы координат, в математике используются и другие способы задания положения точки в пространстве или на плоскости. Чаще всего применяются полярные, цилиндрические и сферические координаты. Все эти системы родственны. В них присутствует центральная точка или полюс, от которого расходятся концентрические окружности (полярная система координат), цилиндры (цилиндрическая система) или сферы (сферические координаты). Положение точки определяется при помощи луча, выходящего из полюса и пересекающего в заданном месте соответствующую окружность, цилиндр или сферу. В такие координаты очень естественно укладываются многие природные формы. Перечисленные криволинейные системы координат идеально приспособлены для отображения форм, построенных вокруг единой центральной точки. Такая организация характерна для многих биологических объектов. Их формы порой самым удивительным образом напоминают фигуры, образуемые в криволинейных координатах достаточно простыми и лаконичными математическими выражениями. Это сходство указывает на то, что тела живых организмов, биологические структуры, образуются по принципам, сходным с принципами построения «полярных» объектов. Живой организм «начинается» из одной исходной точки, и затем развивается и растет во все стороны по определенному математическому закону. По крайней мере такое предположение совсем не противоречит наблюдаемому в природе обилию «математических», «полярных» форм. Природа как бы сама использует полярные координаты, что особенно бросается в глаза на примере растений, примитивных многоклеточных животных и насекомых. Вероятно поэтому фигуры, построенные в полярных координатах, обладают неповторимой эстетической привлекательностью. Они плотно ассоциируются с формами цветов, бабочек, словом, всем тем, что так много удовольствия доставляет нашему взору в живой природе.

Полярная система координат

В полярной системе координат положение точки определяется полярным радиусом R и углом theta , образуемым полярным радиусом с полярной осью. Если в декартовой системе координат предельно простое выражение y=kx определяет прямую линию, то это же выражение, переписанное в форме R=k*theta , уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. В цилиндрической системе к полярному радиусу и углу добавляется еще одна координата — z, которую можно интерпретировать как высоту точки над плоскостью, в которой вращается полярный радиус.

Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы:

Соответственно, для перехода от декартовой системы к полярной применяют формулу:

Фигуры в полярных координатах

Формулы кривых, записанных в полярной системе координат, вычисляются гораздо проще, чем в декартовой. Например, уравнение окружности с радиусом 0.9 вокруг точки отчета выглядит очень просто

R=0.9 , что подразумевает следующие вычисления: где угол theta изменяется от 0 до 2π радиан и определяет декартовы координаты X и Y окружности в полярной системе

Для объяснения вышесказанного приведем небольшой листинг программы, рисующей окружность:

Полярные координаты позволяют рисовать намного более сложные и красивые фигуры. Например, можно нарисовать четырехлистный клевер. Его формула выглядит как R = Cos (2*theta) , где угол theta меняется от 0 до 2π радиан (от 0 до 360 градусов)

Листинг для клевера

Для трехлистного цветка используйте формулу R = Cos (3*theta)

Окружность

Итак, формула R=a определяет обычную окружность, а коэффициент a влияет на ее радиус

«Пируэты» окружности

Возьмем теперь одну окружность и поместим ее внутрь другой. Все кривые, которые будет вычерчивать точка на окружности, катящейся внутри другой окружности, будут относиться к семейству гипоциклоид (от греч. гипо — под, внизу и киклоидес — кругообразный). Как вы думаете, какую траекторию опишет точка окружности, которая катится внутри другой окружности? Как это ни странно звучит, но она может быть даже прямой! Для этого радиус внутренней окружности должен быть в два раза меньше радиуса внешней. Первым это заметил и описал Николай Коперник. Если же радиус внутренней окружности меньше радиуса большой окружности в три раза, то точка опишет кривую Штейнера (дельтоиду).

Уменьшив радиус теперь в четыре раза, мы получим астроиду

Астроида (Astroid)

Астроида (греч. астрон — звезда) — кривая, которая внешне напоминает стилизованное изображение звезды.

Формула x = a* cos(t)^3, y = a* sin(t)^3 рисует астроиду,
где коэффициент a влияет на вытянутость фигуры.

Эпициклоиды

Рассмотрим другой случай. Будем вращать окружность не внутри другой (опорной) окружности, а по ее внешней стороне. Теперь, все получаемые кривые будут относиться к семейству эпициклоиды (греч.эпи — на, над). К таким фигурам относятся кардиодида и улитка Паскаля