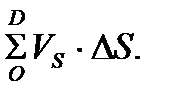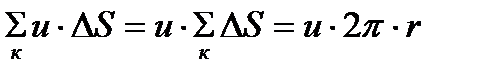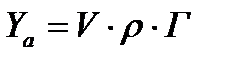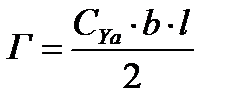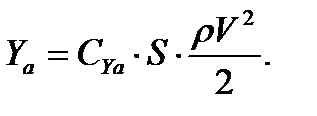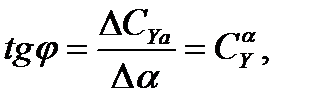Первая попытка исследовать природу подъёмной силы была сделана итальянским учёным и художником Леонардо да Винчи в 1505 г. Он считал, что подъемная сила, поддерживающая птицу, возникает из-за уплотнения воздуха под крыльями.
В 1852г. Магнус, член-корреспондент Петербургской академии наук, провёл серию опытов для объяснения явления отклонения от вертикальной плоскости вращающихся артиллерийских снарядов. Он показал, что поперечная сила, вызывающая это отклонение, возникает из-за взаимодействия двух потоков воздуха:
· набегающего на снаряд;
· вращающегося вместе со снарядом.
Это явление, получившее название эффект Магнуса, было исследовано в 1902-1906 гг Николаем Егоровичем Жуковским.
В 1906году в своей работе « О присоединённых вихрях» он публикует знаменитую «Теорему Жуковского», объясняющую образование подъемной силы.
Важным понятием, лежащим в основе понимания теоремы Жуковского, является вихрь и определяемая им циркуляция.
Рассмотрим обтекание вращающегося цилиндра (рис. 2.10).
| Рис. 2.10. Эффект Магнуса (вращающийся цилиндр) |
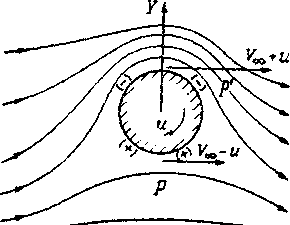
Из-за неравенства скоростей над и под цилиндром возникает разность давлений, порождающая подъемную силу.
Вследствие вязкости воздух увлекается вращающимся цилиндром и создает вокруг него вихрь.
Вихрем будем называть массу воздуха, вращаюуюся вокруг тела.
Вихрь вовлекает во вращение окружающие его массы воздуха и индуцирует (вызывает) скорости
в окружающей среде. Эти окружные скорости называются индуктивными.
Для определения действующих на цилиндр аэродинамических сил его можно заменить вихрем, дающим то же поле скоростей, что и цилиндр.
Замена вращающегося цилиндра вихрем, который Н.Е.Жуковский назвал присоединенным, и позволила Н.Е. Жуковскому создать вихревую теорию крыла. Согласно этой теории подъемная сила крыла возникает вследствие наложения присоединенного вихря на основной поток.
Интенсивность воздействия вихря на окружающую среду, а значит, и величина подъемной силы, определяется циркуляцией скорости.
| Рис. 2.10. К понятию «циркуляция скорости» |
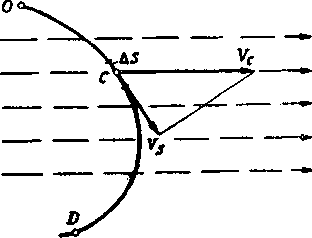
Циркуляция скорости по контуру ОD будет равна сумме элементарных циркуляций.
Г =
Вычислим циркуляцию скорости по замкнутому контуру в виде окружности радиусом r. Индуктивные скорости в каждой точке окружности, создаваемой вихрем, направлены по касательной к этой окружности и постоянны по величине. Поэтому
Г=
Чем больше циркуляция скорости, тем больше разность скоростей и давлений при наложении циркулярного потока на основной поток, т.е. тем больше подъемная сила.
Циркуляция скорости вокруг цилиндра возникает только при его вращении. Циркуляция вокруг крыла возникает самостоятельно, без помощи вращения.
В расчётной схеме Жуковского крылозаменялось вихрем, вокруг которого образуется циркуляция скорости.
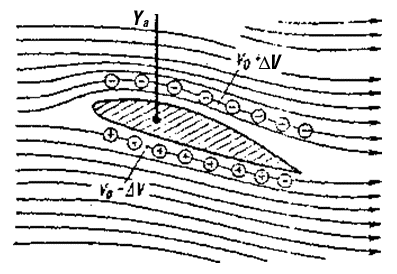
При взаимодействии вихря с плоскопараллельным потоком скорости их суммируются. Над крылом скорость частиц увеличивается, под крылом – уменьшается (рис. 2.11).
Рис. 2.11. Создание подъемной силы
V 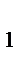
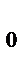
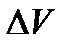
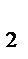
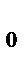
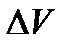
где V 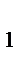
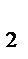
Из-за разности скоростей над крылом и под крылом возникает циркуляция скорости.
В соответствии с законом Бернулли разность скоростей приводит к появлению разности давлений над
и под крылом, т.е. к созданию подъемной силы.
Н. Е. Жуковский вывел формулу для определения величины подъемной силы.
Подъёмная сила единицы длины крыла бесконечного размаха равна произведению циркуляции скорости вокруг профиля крыла на плотность и скорость набегающего потока:
где Г – циркуляция скорости воздуха вокруг профиля крыла;
Yl=1— подъёмная сила для единицы длины крыла.
Теорему Н.Е.Жуковского можно сформулировать так:
Подъемная сила единицы длины крыла бесконечного размаха равна произведению циркуляции скорости вокруг профиля крыла на плотность и скорость набегающего потока.
А для крыла с размахом 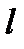
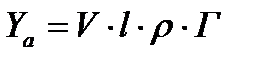
Из формулы видно, что для увеличения подъемной силы крыла при данной скорости нужно увеличить циркуляцию скорости Г. Это достигается увеличением кривизны профиля, управлением пограничным слоем.
Циркуляция скорости Г пропорциональна хорде профиля крыла b и скорости потока и определяется по формуле:
Подставляем Г в формулу Y 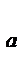
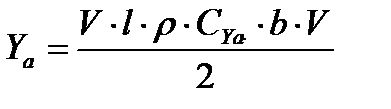
но так как lb = S, то
Таким образом, получили знакомую формулу подъемной силы.
Коэффициент подъемной силы СY 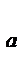
зависимость подъемной силы от формы крыла и его положения в потоке.
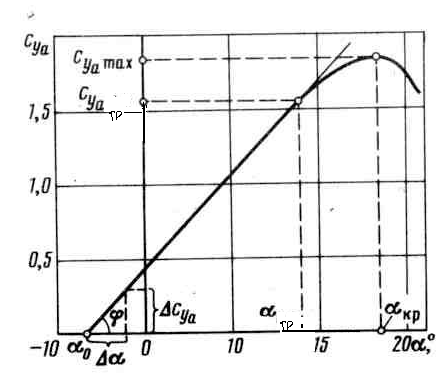
График зависимости коэффициента подъемной силы CY 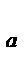
Рис. 2.12. График зависимости Су 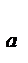
Характерные точки графика:
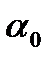
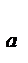
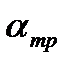
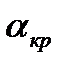
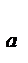
График зависимости CY 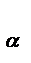
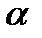
1) при малых углах атаки пограничный слой плотно прилегает к поверхности крыла и зависимость CY 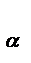
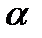
2) 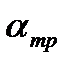
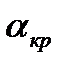
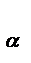
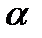
3) α > 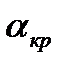
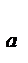
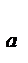
Для симметричного профиля кривая CY 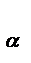
( 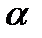
Если угол наклона кривой CY 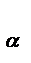
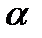
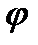
где CY 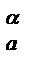
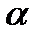
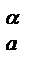
Дата добавления: 2016-12-27 ; просмотров: 12175 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Подъёмная сила крыла ● 4Скачать

Почему и как возникает подъемная сила
Почему могут летать птицы, несмотря на то что они тяжелее воздуха? Какие силы поднимают огромный пассажирский самолет, который может летать быстрее, выше и дальше любой птицы, ведь крылья его неподвижны? Почему планер, не имеющий мотора, может парить в воздухе? На все эти и многие другие вопросы дает ответ аэродинамика — наука, изучающая законы взаимодействия воздуха с движущимися в нем телами.
В развитии аэродинамики у нас в стране выдающуюся роль сыграл профессор Николай Егорович Жуковский (1847—1921) —«отец русской авиации», как назвал его В. И. Ленин.
Заслуга Жуковского состоит в том, что он первый объяснил образование подъемной силы крыла и сформулировал теорему для вычисления этой силы. Им была решена и другая проблема теории полета — объяснена сила тяги воздушного винта. Жуковский не только открыл законы, лежащие в основе теории полета, но и подготовил почву для бурного развития авиации в нашей стране. Он связал теоретическую аэродинамику с практикой авиации, дал возможность инженерам использовать достижения ученых-теоретиков.
В основанных Жуковским лабораториях и в созданных при них кружках выросла целая плеяда ученых, исследователей и конструкторов, обогативших своими трудами и открытиями не только русскую, но и мировую науку. Под научным руководством Жуковского был организован под Москвой Аэрогидродинамический институт. В этом институте удалось провести много весьма ценных исследований.
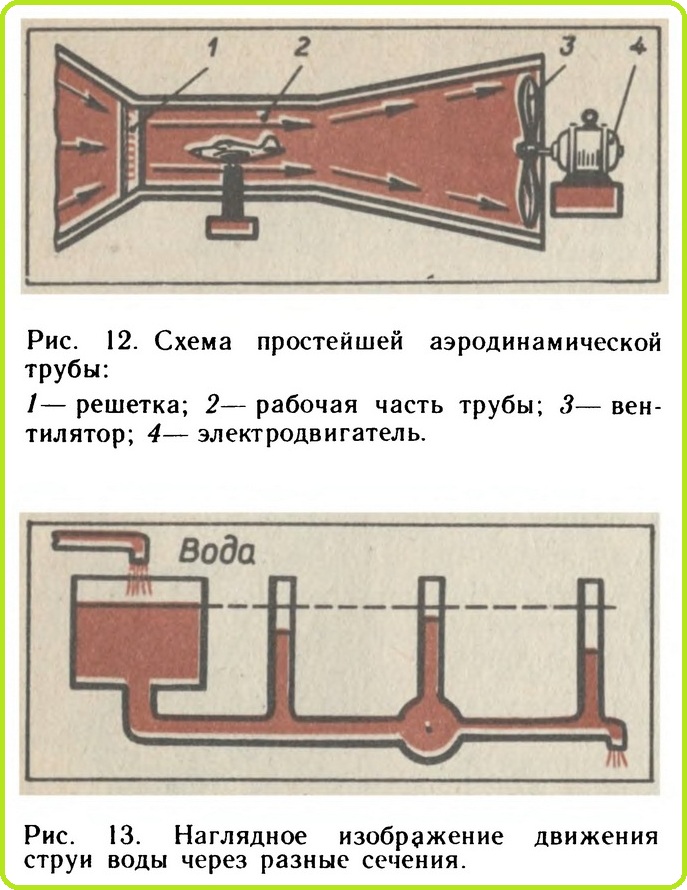
Основным приспособлением, служащим для изучения законов движения тел в воздухе, является аэродинамическая труба. Простейшая аэродинамическая труба представляет собой профилированный канал (рис. 12). В одном конце трубы установлен мощный вентилятор, приводимый во вращение электродвигателем. Когда вентилятор начинает работать, в канале трубы образуется воздушный поток. В зависимости от диаметров канала трубы и воздушного винта и мощности двигателя вентилятора можно получить различные скорости воздушного потока вплоть до сверхзвуковых. Современные аэродинамические трубы достигают гигантских размеров. В их каналах можно помещать для исследования не только модели, но и реальные самолеты.
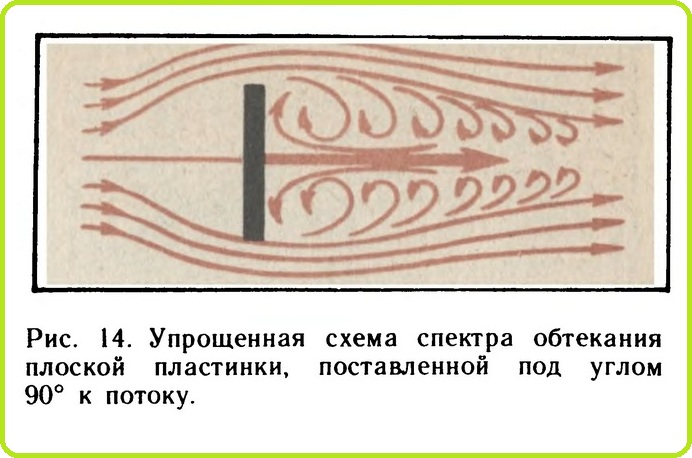
Важнейшими законами аэродинамики являются закон сохранения массы (уравнение неразрывности) и закон сохранения энергии (уравнение Бернулли). Оба эти закона справедливы и для движущегося газа (воздуха), и для жидкости, поэтому проще будет ознакомиться с ними на примере движения воды. На рис. 13 изображена схема прибора, состоящего из открытого резервуара с водой, соединенного с трубкой, имеющий разные сечения. Согласно закону постоянства массы через каждое из этих сечений будет протекать в одну секунду одинаковый объем воды. Но если через неравные сечения в единицу времени протекает одинаковый объем воды, то, значит, через эти сечения вода движется с разными скоростями: чем меньше сечение, тем больше скорость воды (воздуха). В этом можно также убедиться, наблюдая за течением реки. Там, где русло узкое, течение воды быстрее.
Если к потокам жидкости в разных сечениях трубки подключить манометры, то они покажут, что при сужении струи, то есть при увеличении скорости воды (воздуха), давление в струе уменьшается, и наоборот. Это явление, описанное математиком Бернулли, позволяет установить связь между скоростью потока в данном сечении струи жидкости (газа) и давлением в этом же сечении.
Видео:Урок 136. Подъемная сила крыла самолета (часть 2)Скачать

Возникновение подъемной силы
Описанное уравнением Бернулли явление позволяет объяснить возникновение аэродинамических сил, а главное подъемной силы крыла. В литературе это уравнение иногда называют законом Бернулли
Рассмотрим природу возникновения подъемной силы. Опыты, проведенные в аэродинамических лабораториях, позволили установить, что при набегании на тело воздушного потока частицы воздуха обтекают тело. Картину обтекания тела воздухом легко наблюдать, если поместить тело в аэродинамической трубе, в подкрашенном потоке воздуха, кроме того, ее можно сфотографировать. Полученный снимок называют спектром обтекания.
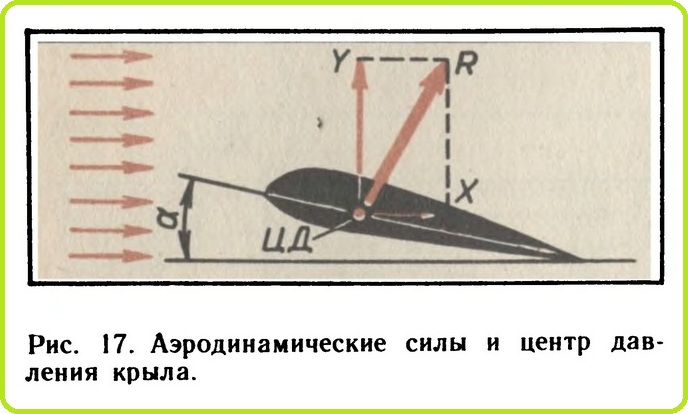
Упрощенная схема спектра обтекания плоской пластинки, поставленной под углом 90° к направлению потока, изображена на рис. 14.
Из рисунка видно, что в этом случае никакой подъемной силы не возникает. Воздух впереди пластинки создает подпор, плотность его струек повышается, а сзади пластинки воздух оказывается разреженным. Повышенной давление воздуха впереди пластинки и разрежение позади нее приводят к тому, что струйки воздуха с силой устремляются в разреженное пространство, закручиваются и образуют сзади пластинки те завихрения, которые мы и видим на спектре.
На рис. 15 дано схематическое изображение спектра обтекания пластинки, поставленной под острым углом к потоку. Под пластинкой давление повышается, а над ней вследствие срыва струй получается разрежение воздуха, т. е. давление понижается. Благодаря образующейся разности давлений и возникает аэродинамическая сила. Она направлена в сторону меньшего давления, т. е. назад и вверх. Отклонения аэродинамической силы от вертикали зависит от угла, под которым пластинка поставлена к потоку. Этот угол получил название угла атаки (его принято обозначать греческой буквой α — альфа).
Свойство плоской пластинки создавать подъемную силу, если на нее набегает под острым углом воздух (или вода), известно уже с давних времен. Примером тому служит воздушный змей и руль корабля, время изобретения которых теряется в веках.
Подъемная сила крыла (обозначим ее Y) возникает не только за счет угла атаки а, но также и благодаря, тому, что поперечное сечение крыла представляет собой чаще всего не симметричный профиль с более выпуклой верхней частью.
Крыло самолета или планера, перемещаясь, рассекает воздух. Одна часть струек встречного потока воздуха пойдет под крылом, другая— над ним (рис. 16). У крыла верхняя часть более выпуклая, чем нижняя, следовательно, верхним струйкам придется пройти больший путь, чем нижним. Однако количество воздуха, набегающего на крыло и стекающего с него, одинаково. значит, верхние струйки, чтобы не отстать от нижних, должны двигаться быстрее. В соответствии с уравнением Бернулли, если скорость воздушного потока под крылом меньше, чем над крылом, то давление под крылом, наоборот, будет больше, чем над ним. Эта разность давлений и создает аэродинамическую силу R (рис. 17), одной из составляющих которой является подъемная сила. Y. Подъемная сила крыла тем больше, чем больше угол атаки, кривизна профиля (его несущие свойства), площадь крыла, плотность воздуха и скорость полета υ, причем от скорости подъемная сила зависит в квадрате. Но следует помнить, что угол атаки должен быть меньше некоторого критического значения акр, при превышении которого подъемная сила падает.
Развивая подъемную силу, крыло всегда испытывает и лобовое сопротивления. Сила лобового сопротивления X направлена по потоку прямо против движения и, значит, тормозит его. Подъемная сила всегда перпендикулярна набегающему потоку. Из рисунка видно, что сила лобового сопротивления X и подъемная сила Y являются составляющими силы R по направлению скорости v и перпендикулярно ей. Сила R называется полной аэродинамической силой крыла. Точку приложения полной аэродинамической силы называют центром давления крыла (ЦД).
Подъемная сила летательного аппарата, уравновешивая его вес, дает возможность осуществлять полет, лобовое же сопротивление тормозит его движение. Отсюда ясно, что крылу надо придать такую форму, чтобы оно развивало как можно большее значение подъемной силы и в то же время давало малое лобовое сопротивление. Число, показывающее, во сколько раз подъемная сила больше лобового сопротивления, называется аэродинамическим качеством и обозначается буквой K.
А теперь подробнее рассмотрим природу возникновения сил сопротивления. Во время купания вы все, конечно, замечали, что в воде двигаться труднее. Это объясняется силой сопротивления воды. Как уже было сказано, воздух — газообразная среда, которая имеет определенную плотность и массу. И, перемещаясь в воздухе, мы также встречаем его сопротивление. Сила, которая мешает нам передвигаться в воздухе, называется силой сопротивления воздуха.
Движется ли тело с некоторой скоростью в неподвижном воздухе или, наоборот, тело неподвижно, а на него набегает поток воздуха с той же скоростью, сила сопротивления воздуха в обоих случаях будет одинаковой. Все дело в том, что воздух и тело движутся один относительно другого.
От каких же причин зависит сопротивление воздуха? Этих причин несколько. На рис. 18 изображена картина обтекания круглой пластинки. Если к этой пластинке спереди сделать конусообразную приставку, которая заполнила бы всю ту область перед пластинкой, где давление было повышено, то спереди давление значительно снизится. И хотя срыв струй и понижение давления позади составного тела будут такими же, как и за пластинкой, все же разность давлений и лобовое сопротивление значительно уменьшатся.
Чтобы избежать срыва струй, следует сделать еще и кормовую конусообразную приставку, заполнив ею всю область пониженного давления за пластиной.
Одновременное использование носовой и кормовой приставок определенной формы позволяет резко снизить лобовое сопротивление по сравнению с лобовым сопротивлением пластинки (примерно в 20—25 раз). Таким образом можно получить тело наиболее выгодной аэродинамической формы. В этом случае поток плавно разделяется передней частью тела, обтекает его и плавно стекает с кормовой части. Тела подобной формы называет удобообтекаемыми. Они и получили наибольшее распространение в авиации.
Что касается влияния размеров тела на сопротивление воздуха, то кажется ясным: чем больше тело, тем сильнее сопротивление. Однако здесь надо уточнить следующее: основной величиной, связанной с размерами тела и определяющей силу сопротивления при его движении, является наибольшая площадь сечения тела, перпендикулярного к направлению движения. какое сечение называется миделевым (рис. 19).
Но еще большее влияние на сопротивление оказывает скорость движения тела в воздухе. При движении тела с небольшой скоростью это сопротивление мало, а с ее увеличением быстро возрастает. При полете самолета на дозвуковых скоростях сопротивление растет прямо пропорционально квадрату скорости. Это значит, что если, например, скорость движения увеличить в два раза, то сопротивление возрастет в четыре раза, если скорость увеличить в три раза, то сопротивление возрастет в девять раз, и т. д. Аналогично, как об этом говорилось выше, скорость влияет и на значение подъемной силы.
Однако для скоростей, близких к скорости звука (340 м/с или 1224 км/ч), из-за влияния сжимаемости воздуха характер обтекания тел изменяется, сопротивление резко возрастает и этот закон уже не действует.
Таким образом, как и подъемная сила, сила лобового сопротивления зависит от угла атаки, формы профиля, плотности воздуха, площади сечения и квадрата скорости, хотя эти зависимости и имеют свои особенности.
Более методичная информация об подъемной силе можно прочитать в материале «Аэродинамические характеристики крыла», а так же, что такое САХ и как найти центр тяжести.
Видео:Подъёмная сила крыла ● 1Скачать

Часть-3. Сказочная Теоретическая аэродинамика
Теория вихря от Жуковского Н.Е., или до какого маразма дожила Физика.
Как я уже писал ранее в Части.1 и Части.2 «Сказочная теоретическая аэродинамика», после того как выяснилось что формула Ньютона непригодна для расчета по нахождению Подъемной Силы (ПС) на крыле, начались теоретические поиски этой самой ПС. Из псевдо уравнения Бернулли следовало: «что там где скорость больше, там Давление меньше», а аэродинамическая труба показывала, что давление меньше над крылом. Логика была убийственной: раз давление над крылом меньше – значит скорость потока над крылом должна быть больше (типо по Бернулли).
Аэродинамисты придумали ускорение потока над крылом, за счет «более длинного пути» над крылом, который верхний поток проходит по отношению к нижнему потоку под крылом. И применили математику: «Скорость – это Расстояние деленное на Время». Фундаментальная Физика эту дурь проглотила.
— — — — — — — —
Совершенно глупая теория о том, что для создания разности давлений (над и под крылом) нужно создать разницу скоростей – родилась.
— — — — — — — —
Эту теорию продолжил и развил будущий «отец Русской авиации» тов. Жуковский Н.Е.(1847-1921) – математик по образованию.
Где то в 1904-1906 году он озвучил мысль о «Бесконечном вихре на бесконечном размахе крыла».
В чем же принципиальное отличие этой теории от теории «типо по Бернулли», а вот в чем:
По Бернулли «аэродинамисты» ускоряли только верхний поток, а нижний поток не трогали, он был базовым.
Маленький пример: предположим, что самолет летит на скорости 50м/сек, тогда:
— нижний поток будет тоже 50м/сек, а верхний как бы 55м/сек. Вот и получается разница в скоростях: 55 – 50 = 5м/сек.
По Жуковскому и ускорялся верхний поток и тормозился нижний.
Маленький пример: предположим, что самолет летит на скорости 50м/сек, тогда:
— нижний поток будет как бы 45м/сек, а верхний как бы 55м/сек. Вот и получается разница в скоростях: 55 – 45 = 10м/сек.
Другими словами теория по Жуковскому была более революционная и более крутая, чем теория по Бернулли, ведь чем больше перепад по скоростям, тем больше будет перепад по давлениям.Теперь когда Вы знаете в чем заключалась «изюминка» теории Жуковского, я Вам расскажу как он к ней пришел.
За основу своей теории Жуковский взял две вещи, а именно:
— теорию сохранения энергии (которую называют «законом»)
— и Эффект Магнуса – 1853год (Генрих Густав Магнус — немецкий физик/химик 1802-1870)
Закон сохранения энергии,. . . напомню подноготную:
В «Законе Сохранения Энергии» условно Полную энергию «для удобства расчета» разбили на Кинетическую и на Потенциальную. Дальше ввели сказочное условие о том, что при переходе Кинетической энергии в Потенциальную и наоборот — потерь нет (т.е. нет сил трения которые потихонечку эту самую энергию «откусывают»). И сделали вывод: Что мол если сил трения НЕТ, то переход одной энергии в другую и наоборот происходит без потерь этой самой энергии. Обозвали эту сказку как «Закон сохранения энергии», и для красного словца заявили, что данный «закон» выполняет везде и всюду на планете Земля, но при этом забыли о том, что на планете Земля нет и не может быть отсутствия сил трения.
Посему: Так называемый «Законе Сохранения Энергии» не является законом Физики, а является теоретической математической выкладкой. Поэтому, какую бы теорию лично Вы не выводили на основании данного «закона», ваша теория будет просто смешна для применения ее в реальных условиях планеты Земля, в условиях постоянно действующих сил трения. А если учесть тот факт что полет самолета – это действие, которое осуществляется именно за счет сил трения, именно от полного аэродинамического сопротивления которое воздух оказывает на крыло, то внедрение «Закона Сохранения Энергии» в аэродинамику – просто смехотворно.
теперь Эффект Магнуса:
При стрельбе ядрами из пушек было замечено, что ядра летят не туда куда их послали, а делают отклонение в ту или в другую сторону от своей «прямолинейной» траектории. В современном мире этот эффект отклонения мы видим на примере футбольного мяча. Вопросом с ядрами в свое время занимался Магнус и вывел теорию, которая затем в последствии была названа его именем.
А мы для простоты восприятия займемся мячом. Давайте представим себе мяч, который летит с право налево, со скоростью 25м/сек (с 3 часов на 9 часов) и при этом вращается по часовой стрелки со скоростью 5м/сек. За счет того что мяч вращается, и за счет того что воздух имеет Вязкость, этот самый воздух в так называемом «пограничном слое» будет вращаться за мячом с той же самой скоростью что и вращается мяч. Как пример этого эффекта мы имеем вращение нашей атмосферы вокруг нашей Земли. Вот это вращение воздуха вокруг мяча и вместе с мячом и называется в физике или вихрем «вокруг мяча» или циркуляцией потока «вокруг мяча», (это кому как больше нравится). Но самое главное что надо знать, что данная циркуляция образуется только тогда когда мяч будет вращаться, а если мяч будет лететь и не будет вращаться, то и никакой циркуляции НЕ БУДЕТ!
Теперь о чем сама теория: А теория о том, что летящий вращающейся мяч имеет два потока и скорости этих потоков надо сложить:
Первый поток – это поток вокруг мяча (от его скорости вращения), а второй поток это поток который набегает на мяч (поток от его скорости полета). Вверху мяча (в районе 12 часов) по нашему условию и набегающий поток от полета, и поток циркуляции: направлены на 3 часа и Складывая их мы получим (25 + 5 = 30м/сек). Внизу мяча (в районе 6 часов) по нашему условию набегающий поток от полета направлен на 3 часа, а поток циркуляции направлен на 9 часов и Складывая их мы получим (25 — 5 = 20м/сек). Таким образом над мячом мы имеем суммарную скорость потока 30м/сек, а под мячом мы имеем суммарную скорость потока 20м/сек. Дальше применяется «типо уравнение Бернулли»: где скорость меньше там, давление больше. По этой причине и происходит смещение мяча из зоны повышенного давления в зону пониженного.
В нашем конкретном случае если мяч рассматривать в горизонтальном полете с боку, то у него появится подъемная сила. Если мяч рассматривать в полете сверху и от нас, то у него появится сила бокового скольжения (смещения)вправо.
Только к НАСТОЯЩЕМУ уравнению Бернулли это не имеет никакого отношения , так как вывод о том, что при увеличении скорости потока давление в потоке падает – это вывод из эффекта Эжекции, который на тот момент был неизвестен Физике, т.к. не был еще открыт. А в наше время эффект Эжекции и под запретом и оболган, т.к. разоблачает всю теоретическую аэродинамику. Ну это другая история …
— — — — — — — — — — — — — — — —
А Эффект Магнуса звучит примерно так: — это физическое явление, возникающее при обтекании движущегося И вращающегося тела потоком жидкости или газа. В результате чего образуется «Сила бокового смещения, которая направлена по нормали к набегающему потоку», в сторону где Скорость вращения совпадает со Скоростью набегающего потока .
— — — — — — — — — — — — — — — —
(Потом ,кстати, из этой фразы: «Сила бокового смещения, которая направлена по нормали к набегающему потоку» и родилось самое тупое заявление всех времен и народов от аэродинамики о том, что Подъемная Сила – ВСЕГДА перпендикулярна набегающему потоку.)
И что же сделал Жуковсктий Н.Е.?
Во времена когда Жуковский писал свой «труд», аэродинамическим трубам уже было лет так за 30. И было известно, что и во время полета, и вовремя обдува крыла ИСКУССТВЕННО СОЗДАННЫМ потоком в аэродинамической трубе — за крылом образуется вихрь.
Давайте представим крыло, которое летит с право налево, со скоростью 50м/сек (с 3 часов на 9 часов) и при этом с задней кромки срывается вихрь направленный ПРОТИВ часовой стрелки со скоростью вращения 5м/сек.
Крыло НЕ вращается, и предполагать Вихрь вокруг не вращающегося крыла по Магнусу — просто глупо. Поэтому Жуковский привлек к своим умозаключениям «Закон Сохранения Энергии».
Логика такая: «Раз с крыла срывается вихрь против часовой стрелки, то для выполнения «Закона Сохранения Энергии» должен быть еще один вихрь, который должен вращаться в обратном направлении, и этот вихрь есть и имеет место быть вокруг крыла.»
Таким образом мы получаем теорию вихря вокруг крыла ПО часовой стрелки(для нашего случая). Верхние потоки в нашем случае складываются (50+5=55м/сек), а нижние потоки в нашем случае вычитаются (50-5=45м/сек). Вот и все, все как с мячом. Вот вам подъемная сила по Жуковскому. Некоторые «особо одаренные физики» крутят ЦИЛИНДРЫ.
Хотите смейтесь, хотите плачьте, а хотите – можете верить во весь этот бред. Это кому как больше нравиться.
Про глупость о том, что Закон сохранения энергии всюду и везде работает на планете Земля, я Вам уже рассказал, а вот про вихрь, который срывается с задней кромки – надо поподробнее.
📸 Видео
Аэродинамика для всех - Часть 8 Горизонтальный полёт Кривые ЖуковскогоСкачать

Кривые ЖуковскогоСкачать

Как летает самолет? Закон Бернулли - Основы авиации #2Скачать

Функция ЖуковскогоСкачать
Подъёмная сила крыла ● 3Скачать

Как крылья создают подъемную силу?Скачать

Расчёт и построение аэродинамических профилей на примере профиля N.A.C.A.Скачать

Урок 135. Применения ур-ния Бернулли (ч.2). Подъемная сила крыла самолета (ч.1)Скачать

Подъёмная сила крыла ● 2Скачать

Подъемная сила крыла Модели Ньютона, Бернулли и ЖуковскогоСкачать

Скамья Жуковского (закон сохранения момента импульса)Скачать

Закон БернуллиСкачать

Великая наука России. Николай ЖУКОВСКИЙ.Скачать

Почему воздушный поток над аэродинамическим профилем движется быстрее, чем под ним?Скачать

Общие основы аэродинамики.Скачать

Аэродинамика для всех - Часть 2 Закон Бернулли, Угол атакиСкачать

Подъемная сила крыла самолета: заблуждение или научный обман "всех времен и народов"?Скачать