Уравнение зависимости ускорения точки от времени (4 видео)

Ускорение при равноускоренном прямолинейном движении

Содержание

теория по физике 🧲 кинематика
Проекция ускорения
Направление вектора ускорения
График ускорения
Уравнение зависимости ускорения точки от времени
Уравнение зависимости ускорения точки от времени
📸 Видео

теория по физике 🧲 кинематика

Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением ( a =const).
Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a .
Единица измерения ускорения — метр в секунду в квадрате (м/с 2 ).
Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график лежит выше оси времени , движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
Если график лежит ниже оси времени , движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t₁ = 1с ускорение a = 2 м/с 2 . В момент времени t₂ = 3 ускорение a = 0 м/с 2 .

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Записать исходные данные.
Записать формулу, связывающую известные из условия задачи величины.
Выразить из формулы искомую величину.
Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

Начальная скорость v₀ = 5 м/с.
Конечная скорость v = 15 м/с.
Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

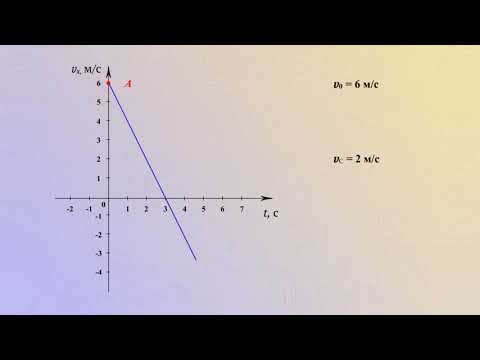
Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
Вычислить ускорение движение тела на этом участке.
Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Записать формулу ускорения.
Записать формулу для вычисления модуля ускорения.
Выбрать любые 2 точки графика.
Определить для этих точек значения времени и проекции скорости (получить исходные данные).
Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Выбираем любые 2 точки графика. Пусть это будут:

t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Уравнение зависимости ускорения точки от времени

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

V (t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.

Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Зависимость перемещения от времени. График s(t) — наклонная линия :

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

V_x — Скорость тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

a_x — Ускорение тела

t — Время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения: v_x = v_xo + a_xt

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

S_x — Перемещение тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

V_x — Скорость тела при равноускоренном движении по прямой

a_x — Ускорение тела

t — Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

Графическое представление неравномерного прямолинейного движения

V(t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости v_x = v_xo + a_xt . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:

В координатах зависимость имеет вид:

Видео:Графики зависимости пути и скорости от времениСкачать

Уравнение зависимости ускорения точки от времени

3.1. Равнопеременное движение по прямой.

3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением:

3.1.2. Ускорение () — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.

В векторном виде:

где — начальная скорость тела, — скорость тела в момент времени t.

В проекции на ось Ox:

где — проекция начальной скорости на ось Ox, — проекция скорости тела на ось Ox в момент времени t.

Знаки проекций зависят от направления векторов и оси Ox.

3.1.3. График проекции ускорения от времени.

При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.):

Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения

3.1.4. Скорость при равнопеременном движении.

В векторном виде:

В проекции на ось Ox:

Для равноускоренного движения:

Для равнозамедленного движения:

3.1.5. График проекции скорости в зависимости от времени.

График проекции скорости от времени — прямая линия.

Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox.

Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; где — изменение скорости за время

Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).

3.1.6. Геометрический смысл площади под графиком в осях

Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом.

На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции:

(3.9)

3.1.7. Формулы для расчета пути

(3.10)

(3.12)

(3.11)

(3.13)

(3.14)

Все формулы, представленные в таблице, работают только при сохранении направления движения, то есть до пересечения прямой с осью времени на графике зависимости проекции скорости от времени.

Если же пересечение произошло, то движение проще разбить на два этапа:

до пересечения (торможение):

После пересечения (разгон, движение в обратную сторону)

В формулах выше — время от начала движения до пересечения с осью времени (время до остановки), — путь, который прошло тело от начала движения до пересечения с осью времени, — время, прошедшее с момента пересечения оси времени до данного момента t, — путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t, — модуль вектора перемещения за все время движения, L — путь, пройденный телом за все время движения.

3.1.8. Перемещение за -ую секунду.

За время тело пройдет путь:

Тогда за -ый промежуток тело пройдет путь:

За промежуток можно принимать любой отрезок времени. Чаще всего с.

Если то

Тогда за 1-ую секунду тело проходит путь:

Если внимательно посмотрим, то увидим, что и т. д.

Таким образом, приходим к формуле:

Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорением движется тело. Подчеркнем, что это соотношение справедливо при

3.1.9. Уравнение координаты тела при равнопеременном движении

Знаки проекций начальной скорости и ускорения зависят от взаимного расположения соответствующих векторов и оси Ox.

Для решения задач к уравнению необходимо добавлять уравнение изменения проекции скорости на ось:

3.2. Графики кинематических величин при прямолинейном движении

3.3. Свободное падение тела

Под свободным падением подразумевается следующая физическая модель:

1) Падение происходит под действием силы тяжести:

2) Сопротивление воздуха отсутствует (в задачах иногда пишут «сопротивлением воздуха пренебречь»);

3) Все тела, независимо от массы падают с одинаковым ускорением (иногда добавляют — «независимо от формы тела», но мы рассматриваем движение только материальной точки, поэтому форма тела уже не учитывается);

4) Ускорение свободного падения направлено строго вниз и на поверхности Земли равно (в задачах часто принимаем для удобства подсчетов);

3.3.1. Уравнения движения в проекции на ось Oy

В отличии от движения по горизонтальной прямой, когда далеко не всех задач происходит смена направления движения, при свободном падении лучше всего сразу пользоваться уравнениями, записанными в проекциях на ось Oy.

Уравнение координаты тела:

Уравнение проекции скорости:

Как правило, в задачах удобно выбрать ось Oy следующим образом:

Ось Oy направлена вертикально вверх;

Начало координат совпадает с уровнем Земли или самой нижней точкой траектории.

При таком выборе уравнения и перепишутся в следующем виде:

3.4. Движение в плоскости Oxy.

Мы рассмотрели движение тела с ускорением вдоль прямой. Однако этим равнопеременное движение не ограничивается. Например, тело, брошенное под углом к горизонту. В таких задачах необходимо учитывать движение сразу по двум осям:

Или в векторном виде:

И изменение проекции скорости на обе оси:

3.5. Применение понятия производной и интеграла

Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.

где A, B и то есть постоянные величины.

Теперь посмотрим, как понятие производной и интеграла применимо к физическим величинам. В математике производная обозначается «’», в физике производная по времени обозначается «∙» над функцией.

то есть скорость является производной от радиус-вектора.

Для проекции скорости:

то есть ускорение является производной от скорости.

Для проекции ускорения:

Таким образом, если известен закон движения то легко можем найти и скорость и ускорение тела.

Теперь воспользуемся понятием интеграла.

то есть, скорость можно найти как интеграл по времени от ускорения.

то есть, радиус-вектор можно найти, взяв интеграл от функции скорости.

Таким образом, если известна функция то легко можем найти и скорость, и закон движения тела.

Константы в формулах определяются из начальных условий — значения и в момент времени

3.6. Треугольник скоростей и треугольник перемещений

3.6.1. Треугольник скоростей

В векторном виде при постоянном ускорении закон изменения скорости имеет вид (3.5):

Эта формула означает, что вектор равен векторной сумме векторов и Векторную сумму всегда можно изобразить на рисунке (см. рис.).

В каждой задаче, в зависимости от условий, треугольник скоростей будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

3.6.2. Треугольник перемещений

В векторном виде закон движения при постоянном ускорении имеет вид:

При решении задачи можно выбирать систему отсчета наиболее удобным образом, поэтому не теряя общности, можем выбрать систему отсчета так, что то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда

то есть вектор равен векторной сумме векторов и Изобразим на рисунке (см. рис.).

Как и в предыдущем случае в зависимости от условий треугольник перемещений будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.