Для равновесия между жидкостью и паром уравнение Клапейрона-Клаузиуса может быть получено следующим образом.
Согласно второму закону термодинамики если система находится в равновесии, то при данных условиях (Р, Т) работа не совершается
то есть свободные энергии Гиббса чистой жидкости и её пара равны (это условия равновесия).
Изменим одно из условий, определяющих равновесие, например, температуру (то есть нагреем систему на Т), в результате этого установится новое давление, новое равновесие жидкость-пар:
Если изменение внешнего параметра произойдет на бесконечно малую величину — dT, то и изобарно-изотермические потенциалы изменятся на бесконечно малую величину:
Изобарно-изотермический потенциал представляет собой свободную энергию системы и является функцией давления и температуры:
поэтому с его помощью можно установить количественную зависимость между давлением насыщенного пара и температурой.
После подстановки (6) в (5) имеем в состоянии равновесия
VжdP — SжdT = VпdP — SпdT (7)
откуда 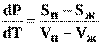
где (Sп — Sж) и (Vп— Vж) — изменение соответственно энтропии и объема системы при переходе вещества из жидкого в парообразное состояние. Согласно второму закону термодинамики изменение энтропии системы при испарении равно приведенной теплоте испарения
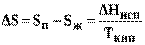
Подставив выражение (9) в (8) получим
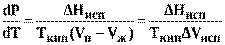
где ∆Hиспи ∆Vисп— соответственно изменение энтальпии и объема при испарении, аTкип— температура кипения.
Уравнение (10) называется уравнением Клапейрона-Клаузиуса. Согласно (10) наклон линий на фазовой диаграмме воды (рис. 1) определяется знаком производнойdP/dTили обратной ей величиныdT/dP— характеризующей изменение температуры с увеличением давления.
Из фазовых переходов рассмотрим испарение и плавление. Теплота испарения — перехода жидкой фазы в газообразную положительна. Молярной теплотой испаренияназывается количество тепла, затраченное на испарение одного моля жидкого вещества. Объем газа при испарении всегда больше соответствующего объема жидкости, то есть в уравнении (10)Vп> Vж. ПоэтомуdP/dT, а значит, иdT/dPтакже всегда положительны (dT/dP> 0). Следовательно, температура испарения всегда повышается с ростом давления (криваяОКна рис. 1 или см. табл. 1 Приложения). С увеличением температуры давление насыщенного пара над жидкостью возрастает, принимая максимальное значение при критической температуре. Последняя является предельной температурой (например, для воды она равна 374,12 о С) при которой возможно равновесие между жидкой и паровой фазой вещества. При более высоких температурах вещество может находиться только в газообразном состоянии, и понятие насыщенного пара теряет свой смысл.
Теплота плавления — перехода твердой фазы в жидкую также всегда положительна.
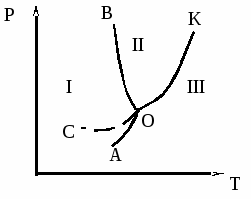
Области: 1 — твердая фаза (лед); II- жидкость; III — пар.
Кривые: АО — возгонки; ОК — испарения; ОВ — плавления.
О — тройная точка, отвечающая равновесию трех фаз.
Объем жидкой фазы в общем случае может быть больше или меньше объёма того же количества твердой фазы. Отсюда в соответствии с уравнением (10) вытекает, что величина dP/dTили обратная её величинаdT/dP, может быть положительной или отрицательной. Это значит, что температура плавления может повышаться или снижаться с увеличением давления. ВеличинаdT/dPположительна для большинства веществ. Она имеет отрицательное значение лишь для воды, висмута и немногих других веществ, для которых плотность жидкости при температуре плавления больше плотности твердой фазы (Vж—Vт) > 0 (например, для воды мольный объём в парообразном состоянии при н.у.Vп≈ 22400 см 2 , а в жидком состоянииVж≈ 18 см 3 ), то без большой погрешности можно пренебречь величинойVжи принять, что∆Vисп≈Vп.
2) При не слишком высоких давлениях и температурах (вдали от критических) можно применять уравнение состояния для идеальных газов и к реальным системам. Погрешность, получаемая при этом, оказывается незначительной.
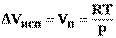
Подставив (11) в (10) получим:
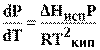
которое после преобразования
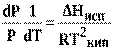
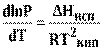
Теплота испарения зависит от температуры: с повышением температуры теплота испарения понижается. При критической температуре теплота испарения равна нулю. Однако при температурах, далеких от критической, изменения∆Ниспс температурой не очень велики. В не слишком большом интервале температур∆Ниспможно считать постоянной.
Интегрирование уравнения Клапейрона-Клаузиуса (14) в пределах температур Т1 иТ2, которым отвечают давленияР1 иР2 при постоянном значении ∆Нисп, дает
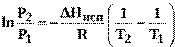
или при переходе к десятичным логарифмам
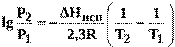
(R— универсальная газовая постоянная равная 8,314 Дж/моль · К).
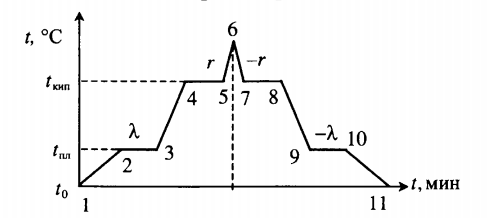
Уравнения (15), (16) позволяют рассчитать теплоту испарения. Для этого по экспериментальным данным строят зависимость lnP=f(1/T) илиlgP=f(1/T) и на полученной прямой выбирают две точки (рис. 2). Подставляют соответствующие этим точкам значения логарифма давления и обратной температуры в уравнение (17):
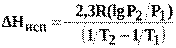
Значение∆Нисппо уравнению (17) зависит от взятого интервала температур и тем ближе к истинному, чем этот интервал меньше. Однако для такого вычисления требуется весьма точное измерение температуры кипения и давления пара.
Для вычисления∆Ниспв относительно широком интервале температур (50. 100 о С) следует выбирать точки, наиболее точно укладывающиеся на прямуюlgP=f(1/T).
Температура кипения жидкости, давление пара при данной температуре и теплота испарения являются специфическими константами вещества, значения которых необходимы для многих теоретических и практических расчетов. На основе этих данных можно определять чистоту химических веществ, провести расчет разделения смесей путем перегонки, рассчитать энергетические затраты на испарение жидкости, необходимые для проведения реакции в газовой фазе.
- Зависимость теплоты испарения жидкости от температуры
- Зависимость теплоты испарения жидкости от температуры
- Фазовые переходы и уравнение теплового баланса
- теория по физике 🧲 термодинамика
- Плавление и отвердевание
- Парообразование и конденсация
- Тепловые процессы при нагревании и охлаждении
- Частные случаи тепловых процессов
- Уравнение теплового баланса
- Взаимные превращения механической и внутренней энергии
- Примеры КПД
- 📹 Видео
Видео:Кипение, удельная теплота парообразования. 8 класс.Скачать

Зависимость теплоты испарения жидкости от температуры
Видео:Физика 8 класс (Урок№8 - Испарение и конденсация. Насыщенный пар. Кипение.)Скачать

Зависимость теплоты испарения жидкости от температуры
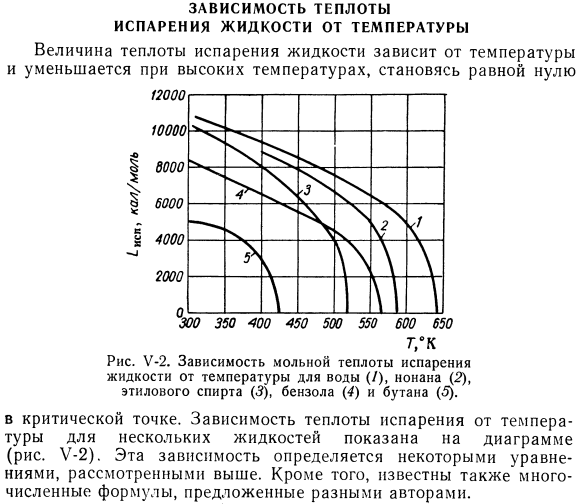
Зависимость теплоты испарения жидкости от температуры. Теплота испарения жидкости зависит от температуры, при высоких температурах она уменьшается и становится равной нулю В важный момент.
Теплота испарения с увеличением давления, а следовательно, и температура кипения жидкости, уменьшается. Людмила Фирмаль
- Температурная зависимость некоторых жидкостей от теплоты испарения показана на рисунке (рисунок U-2). Эта зависимость определяется некоторыми из рассмотренных выше уравнений. Кроме того, известно также большое количество формул, предложенных разными авторами.
Поэтому значения теплот испарения определяют обычно опытным путем и при тех или иных тепловых расчетах требуемые данные берут из справочных таблиц. Людмила Фирмаль




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Насыщенный пар. Зависимость давления пара от температуры | Физика 10 класс #35 | ИнфоурокСкачать

Фазовые переходы и уравнение теплового баланса
теория по физике 🧲 термодинамика
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Видео:Парообразование и конденсация. Практическая часть - решение задачи. 8 класс.Скачать

Плавление и отвердевание
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
Определение Отвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Видео:Урок 123 (осн). Кипение. Удельная теплота парообразованияСкачать

Парообразование и конденсация
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
Определение Конденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Видео:8 класс, 8 урок, Испарение и конденсация Удельная теплота парообразованияСкачать

Тепловые процессы при нагревании и охлаждении
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
| Процесс | Что происходит | Количество выделенной теплоты | ||||||||||||||||||||||||||||||||||||||||||||||||
| 1–2 | Нагревание твердого тела | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2–3 | Плавление при температуре плавления (tпл) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3–4 | Нагревание жидкости | |||||||||||||||||||||||||||||||||||||||||||||||||
| 4–5 | Кипение при температуре кипения (tкип) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 5–6 | Нагревание пара | |||||||||||||||||||||||||||||||||||||||||||||||||
| 6–7 | Охлаждение пара | |||||||||||||||||||||||||||||||||||||||||||||||||
| 7–8 | Кипение при температуре кипения (tкип) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 8–9 | Охлаждение жидкости | |||||||||||||||||||||||||||||||||||||||||||||||||
| 9–10 | Отвердевание при температуре плавления (tпл) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 10–11 | Охлаждение твердого тела |
| Что происходит | График | Формула количества теплоты | |||||||||||||||||||||||||||||||||||||
| Полностью растопили лед, имеющий отрицательную температуру. | 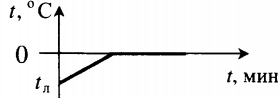 | ||||||||||||||||||||||||||||||||||||||
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 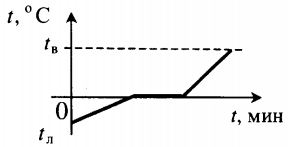 | ||||||||||||||||||||||||||||||||||||||
| Взяли лед при температуре 0 о С и полностью испарили. | 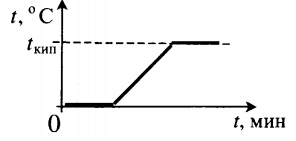 | ||||||||||||||||||||||||||||||||||||||
| Взяли воду при комнатной температуре и половину превратили в пар. | 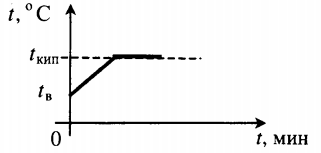 |
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 о С. |
| Объем воды 5 л | m = 5 кг, так как: m = ρ V =10 3 · 5 · 10 − 3 м 3 = 5 к г Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 о С, чтобы превратить его в воду и нагреть ее до температуры +30 о С?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q = Q 1 + Q 2 + Q 3
Q = c л m ( 0 − t 1 ) + λ m + c в m ( t 2 − 0 )
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙10 3 Дж/кг.
Q = 2050 · 2 ( 0 − ( − 10 ) ) + 333 , 5 · 10 3 · 2 + 4220 · 2 · 30 = 961200 ( д ж ) = 961 , 2 ( к Д ж )
Видео:Физика. 8 класс. Зависимость температуры кипения от внешнего давления /03.11.2020/Скачать

Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Q о т д = − Q п о л
Отданное количество теплоты меньше нуля (Qотд 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 о С. Учтите, что лед плавится, если он находится при температуре 0 о С и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 о С, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 о С, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 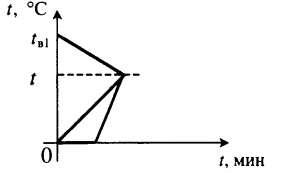 Уравнение теплового баланса: Уравнение теплового баланса:Q 1 + Q 2 + Q 3 = 0 c в m в 1 ( t − t в 1 ) + c в m в 2 ( t − 0 ) + λ m л + c в m л ( t − 0 ) = 0 | ||||||||||||||
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 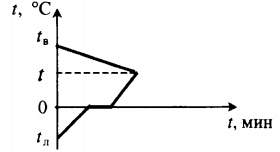 Уравнение теплового баланса: Уравнение теплового баланса:c в m в ( t − t в ) + c л m л ( 0 − t л ) + λ m л + c в m л ( t − 0 ) = 0 | ||||||||||||||
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 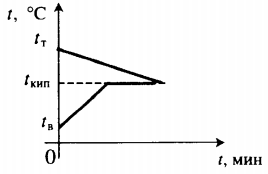 Уравнение теплового баланса: Уравнение теплового баланса:c т m т ( 100 − t т ) + c в m в ( 100 − t в ) + r m п = 0 | ||||||||||||||
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 о С. | 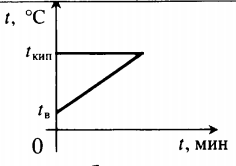 Уравнение теплового баланса: Уравнение теплового баланса:− r m п + c в m в ( 100 − t в ) = 0 | ||||||||||||||
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 о С. |  Уравнение теплового баланса: Уравнение теплового баланса:− r m п + c в m п ( t − t к и п ) + λ m л + c в m л ( t − t п л ) = 0 Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 о С, долили 3 л кипятка. Какая температура воды установилась? Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому: c m 1 ( t − t 0 ) = − c m 2 ( t − t к и п ) m 1 ( t − t 0 ) = − m 2 ( t − t к и п ) m 1 t + m 2 t = m 1 t 0 + m 2 t к и п ( m 1 + m 2 ) t = m 1 t 0 + m 2 t к и п t = m 1 t 0 + m 2 t к и п m 1 + m 2 . . t = 2 · 25 + 3 · 100 2 + 3 . . = 350 5 . . = 70 ( ° C ) Видео:Урок 124 (осн). Зависимость температуры кипения жидкости от давленияСкачать  Взаимные превращения механической и внутренней энергииЕсли в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале. Частные случаи закона сохранения энергии
|


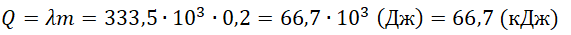
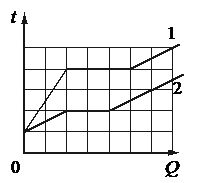 На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.
На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.










