Уравнение зависимости скорости от времени по графику

Видео:Графики зависимости пути и скорости от времениСкачать

Уравнение зависимости скорости от времени по графику

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

V (t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.

Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Зависимость перемещения от времени. График s(t) — наклонная линия :

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

V_x — Скорость тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

a_x — Ускорение тела

t — Время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения: v_x = v_xo + a_xt

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

S_x — Перемещение тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

V_x — Скорость тела при равноускоренном движении по прямой

a_x — Ускорение тела

t — Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

V(t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.

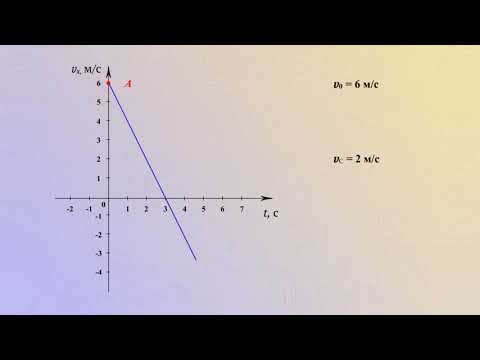
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости v_x = v_xo + a_xt . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:

В координатах зависимость имеет вид:

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Графики прямолинейного движения

Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.

Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.

Будем отдельно рассматривать:

• движение без ускорения (равномерное), и
• движение с ускорением (неравномерное).

1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec =0).

2). Неравномерное движение — скорость меняется и появляется ускорение.

Пусть ускорение есть и, оно не изменяется: (vec =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:

• Равноускоренное движение — скорость тела увеличивается.
• Равнозамедленное движение — скорость уменьшается.

Примечание: Когда изменяется скорость, всегда появляется ускорение!

Движение будем изображать графически, используя две перпендикулярные оси.

На графиках будем откладывать:

• по горизонтали — время в секундах.
• по вертикали — координаты тела, или проекции скорости и ускорения.

Для каждого вида движения получим три графика. Графики будем называть так:

1. x(t) – зависимость координаты от времени;
2. v(t) – зависимость проекции скорости от времени;
3. a(t) – зависимость проекции ускорения от времени.

Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.

Видео:7 класс, 6 урок, Графики зависимости пути и скорости от времениСкачать

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют

Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_]

Скорость и ускорение неподвижного тела равны нулю:

Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.

Видео:Расчет ускорения по графикуСкачать

Скорость не меняется — движение равномерное

Разберём равномерное движение в направлении оси (рис. 2а).

Начальная координата тела – это точка (x_), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».

Красной стрелкой обозначено направление, в котором тело движется.

Примечание: Тело движется туда, куда направлен вектор его скорости.

Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).

Уравнение, описывающее изменение координаты выглядят так:

[ x = x_ + v cdot t ]

Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:

Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:

Равномерное движение в направлении противоположном оси

Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.

Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.

Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.

А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.

Видео:Физика - уравнения равноускоренного движенияСкачать

Равноускоренное движение в направлении оси, скорость увеличивается

Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.

Уравнение, которое описывает квадратичное изменение координаты, выглядит так:

Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:

[ v = v_ + a cdot t ]

Ускорение есть (рис. 4г) и оно не меняется:

Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.

Примечания:

1). Координата «x» будет изменяться:

• по линейному закону, когда скорость не меняется — остается одной и той же.
• по квадратичному закону, когда скорость будет изменяться (расти, или убывать).

2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.

3). Квадратичный закон – это уравнение второй степени, на графике — парабола.

4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.

Равноускоренное движение против оси

Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).

Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).

Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec) и (vec) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.

Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.

Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Скорость уменьшается — движение равнозамедленное

Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).

Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).

А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).

Равнозамедленное движение против оси

Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).

Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).

Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.

Видео:Физика 7 кл (2013 г) Пер §17 Упр 4 №4 . График зависимости скорости равномерного движения тела от врСкачать

Выводы

1). Все, что лежит:

• выше оси t – положительное;
• ниже оси t – отрицательное;
• на горизонтальной оси t – равно нулю.

2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).

3). Если скорость не меняется, ускорения нет.

• График x(t) координаты – это прямая линия.
• График v(t) скорости – горизонтальная прямая.
• График a(t) ускорения лежит на оси t.

4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.

• График x(t) координаты – это правая ветвь параболы.
• График v(t) скорости – наклонная прямая.
• График a(t) ускорения – горизонтальная прямая.

5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.

• График x(t) координаты – это левая ветвь параболы.
• График v(t) скорости – наклонная прямая.
• График a(t) ускорения – горизонтальная прямая.

Видео:Решение графических задач на равномерное движениеСкачать

Равномерное прямолинейное движение

Всё в мире находится в движении.

Каждый день, когда мы выходим из дома, мы стараемся рассчитать, насколько быстро доберемся до школы или работы.

Может, однажды мы захотим научиться чему-то новому и купим машину.

А физика объяснит тебе, как не попасть в аварию и как всюду успевать.

Видео:Уравнение движенияСкачать

Равномерное прямолинейное движение — коротко о главном

Сегодня ты узнал:

А еще ты научился решать задачи разного уровня сложности!

Ой, я что, не сказал? Там сложные были!

Ты, наверное, и не заметил 😉

Видео:Физика-9. "График проекции скорости"Скачать

О том, как решить основную задачу механики

Мы помним, что основная задача механики – указать положение тела в пространстве в любой момент времени, не только в настоящем, но и в будущем.

Итак, что нужно знать для того, чтобы найти положение тела в пространстве?

Неплохо было бы знать, где оно находилось в начале своего движения, его начальные координаты. Ведь нам важно, откуда мы выдвигаемся в путь.

Зависят ли начальные координаты тела от времени? Совсем нет: мы просто принимаем то, что тело где-то есть.

А еще нам важно знать, как далеко оказалось тело от своего начального положения и куда вообще двигалось. Важно знать перемещение этого тела.

Давай опробуем свои силы! Думаю, мы уже готовы решить главную задачу!

Рассмотрим какое-то тело. Оно подвигалось, изменило свое положение, оказалось в другой точке.

Назовем ее конечной и постараемся найти ее координаты, то есть узнать положение тела после совершенного им перемещения.

Помним, что перемещение – вектор, поэтому изобразим его:

Уже сейчас мы можем указать начальные координаты тела! Нет чисел – не пугаемся, используем буквы:

Нам нужно узнать конечное положение тела. Отметим координаты тела в конце, их нам и нужно найти, чтобы определить положение тела в конце:

Но как найти эти координаты, зная лишь начальное положение тела и его перемещение? Как нам попасть из (<_>) в (x) и из (<_>) в (y) ?

Все очень просто! Если есть вектор, то какая-нибудь проекция-то найдется, правда?

Теперь ответить на вопрос, как добраться из начала в конец становится очень легким: просто нужно прибавить к начальной точке проекцию перемещения для нужной оси!

То есть положение точки в любой момент времени можно записать так:

Поздравляю! Мы только что решили основную задачу механики!

Правда, сделали это в общем виде… Но перемещение ведь может быть очень разнообразным! Как вообще его найти? Не всегда же оно будет дано!

Это зависит от движения тела.

Видео:Скорость прямолинейного равноускоренного движения. График скорости | Физика 9 класс #6 | ИнфоурокСкачать

Равномерное прямолинейное движение

Определение равномерного прямолинейного движения

Самым простым движением по праву считается равномерное прямолинейное движение. Мы начнем с него.

Давай попробуем дать ему определение.

Всегда стоить помнить, что знать определения наизусть вовсе не обязательно. Главное – научиться строить его самостоятельно.

Успех любого хорошего определения заключается в правильной его структуре.

Равномерное прямолинейное движение – это движение. Мы нашли главное слово нашего определения. Давай развивать его.

Мы уже знаем, что такое движение. Давай дополним это определение.

Что значит равномерное? Равная мера… Но что является этой самой равной мерой?

Тело проходит равные пути. Логично, что происходит это за какие-то промежутки времени.

А за какие промежутки? За равные. За секунду, за минуту, за час. Не обязательно за ОДНУ секунду, ОДНУ минуту, ОДИН час. Равными промежутками времени могут быть, например, три часа или две секунды.

Но что значит прямолинейное? Можно сказать, что это движение по прямой. Но давайте объясним это, исходя из уже знакомых нам понятий.

Представь: какое-то тело движется, у нас в руках секундомер.

Прошла секунда – тело переместилось на метр. Еще секунда – еще метр. В том же направлении.

То есть тело совершает равные перемещения!

Равномерное прямолинейное движение — такое движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

С перемещением намного проще объяснить, почему за равные промежутки времени можно принимать абсолютно любое количество единиц времени.

Пусть тело совершает за 1 секунду перемещение (vec).

Тогда за две секунды совершает перемещение (2vec):

Будет ли тело все еще совершать равные перемещения за каждые 2 секунды? Конечно! Давай посмотрим:

Скорость

Равномерное прямолинейное движение тоже бывает разным: быстрым и медленным. Чтобы охарактеризовать его, существует скорость.

Чем большее перемещение совершает тело за промежуток времени, тем больше его скорость. Это очевидно: за одно и то же время гепард преодолевает расстояние во много раз большее, чем термит.

То есть скорость прямо пропорциональна перемещению!

А еще мы помним, что нам действительно важно направление скорости, ведь нам важно направление движения. То есть скорость – величина векторная. Давай убедимся в этом.

Скорость равномерного прямолинейного движения есть физическая величина, равная отношению вектора перемещения ко времени, за которое оно произошло.

Запишем это в виде формулы:

Векторы с обеих сторон, верно, но… Мы ведь учились умножать векторы, а не делить их. При делении тоже вектор получается?

Да. Ведь любое деление можно представить в виде умножения, смотри:

Время – скалярная величина. Оно не имеет направления. Поэтому можно сказать, что скорость есть перемещение, умноженное на скаляр, то есть тоже вектор! Более того, вектор перемещения и скорости сонаправлены.

Подробнее о свойствах векторов можно прочитать в Большой теории по векторам.

Помнишь, мы чуть выше выясняли, будет ли тело все так же совершать одинаковые перемещения за 2 секунды, а не за одну? Причем эти перемещения сами будут в два раза больше. Значит отношение останется прежним, вот так:

Отсюда делаем вывод:

Скорость равномерного прямолинейного движения постоянна.

Как это записать? Кажется, очевидно, но это «задачка со звездочкой». Вот так:

Мы не можем приравнять векторную величину к скалярной. Поэтому над константой тоже нужно ставить вектор.

Решение основной задачи механики для равномерного прямолинейного движения

Из уравнения скорости можно легко выразить перемещения, что сделает нас на шаг ближе к конкретному решению основной задачи. Давай сделаем это:

Из свойств векторов мы помним, что это будет справедливо и для проекций:

Стоп-стоп-стоп… Мы что, можем уже с помощью этого определить положение точки?

Да, почему нет? Просто подставим это вместо проекций перемещения туда, где мы решали основную задачу механики в общем виде:

Обычно в задачах по физике мы стараемся выбрать оси так, чтобы было проще работать с проекциями. Мы стараемся расположить их так, чтобы как можно больше векторов располагалось параллельно один осям и перпендикулярно другим, вот так:

Проекция перемещения на ось Y будет равняться нулю, мы можем не обращать на нее внимания.

По оси Y тело вообще не меняло своего положения, верно?

Именно поэтому в задачах чаще всего мы будем использовать упрощенный вариант нахождения конечного положения тела. Его координата будет описана лишь одним числом.

То есть используем лишь одну ось:

Работаем с проекциями. Настораживаемся. Вспоминаем о знаках.

Здесь все просто: если проекция скорости положительна, тело движется вдоль оси. Если она отрицательна, тело движется против оси.

Помни, что работаем мы с координатной осью! Начальное положение тела тоже может быть отрицательным. Это зависит лишь от того, как расположено тело относительно начала координат:

Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Графики равномерного прямолинейного движения

Построение графика

Очень важно уметь описывать движение графиком. Это может значительно упростить решение задачи.

Давай посмотрим, как с помощью графика описать равномерное прямолинейное движение.

Любой график – множество точек, который показывает зависимость одного значения от другого. Эта зависимость определяется каким-то уравнением.

Например, когда мы строим параболу, мы руководствуемся уравнением (y=<^>). Как еще это можно записать?

Вот так: (f(x)=<^>). Это показывает, что функция (f) зависит от значения (x).

Давай аналогично составим график движения тела. Вспомним то главное уравнение:

Иными словами, это график зависимости координаты тела от времени. Давай так и запишем:

Начинаем работать с уравнением. Предположим, что нам известна проекция скорости и начальное положение тела. Работать с конкретными числами удобнее.

Тогда уравнение имеет вид: (x=3+0.5cdot t)

Нарисуем оси и обозначим их. Так как у нас даны единицы измерения (метры и секунды), мы обязательно должны подписать их рядом с названиями осей!

Теперь можем взять и рассмотреть положение тела в любую секунду: хоть в первую, хоть в двенадцатую!

Отметим точки и соединим их. Получим график движения.

А теперь вопрос на засыпку: может ли время быть отрицательным?

Могу ли я указать положение тела в минус третью секунду? Могу.

Для этого стоит помнить, что «нулевая» секунда – момент, когда мы запускаем секундомер, когда мы только начинаем наблюдать за телом. Но оно могло двигаться и до того, как мы включили таймер, верно?

Давай покажем движение тела до наших наблюдений пунктирной линией:

Зачастую точки пересечения графика с осями несут в себе очень важную информацию!

Например, когда мы только включили секундомер ((t=0)с), тело находилось в начальном положении ((<_>=3)м), и это видно по графику!

А когда координата тела была равна нулю?

Все очень просто: за 6 секунд до того, как мы включили секундомер! Прямая пересекает ось времени в точке -6.

Итак, мы выяснили, что…

График равномерного прямолинейного движения представляет собой прямую.

Точка пересечения ее с осью Х есть координата в начальный момент времени.

Точка пересечения с осью времени показывает ту секунду, когда тело находится в начале координат.

И действительно, само уравнение (x=<_>+<_>cdot t) уже напоминает стандартное уравнение прямой, которое мы изучаем на математике: (y=kx+m), где (m) — точка пресечения графика с осью Х, а (k) — коэффициент наклона прямой.

В нашем случае роль коэффициента наклона играет проекция скорости.

Зависимость графика от проекции скорости

Давай изобразим несколько графиков в общем виде, то есть без каких-либо конкретных значений. Например, пусть у нас есть два движущихся тела, вот так:

Чем отличаются движения этих двух тел?

Ну, прежде всего, у них разные начальные положения. Ладно.

А что насчет проекции скорости?

Рассмотрим первое тело. С течением времени оно все больше удаляется от начала координат. А вот второе к нему приближается: оно даже достигает начала координат через некоторое время (когда пересекает ось).

Значит, первое тело идет вдоль оси, а второе против нее, то есть к началу! Мы помним, что это определяет знак проекции скорости.

А именно: проекция скорости первого тела положительна. Проекция скорости второго тела отрицательна.

Со знаками разобрались. А как быть, если попросят узнать, какая проекция скорости больше?

Рассмотрим следующий график. Чтобы было легче его анализировать, представим, что два тела имеют одинаковое положение, когда мы включаем секундомер:

Чтобы понять, чья скорость больше, рассмотрим определенный промежуток времени, отделим его вертикальной пунктирной линией. А еще обозначим начальную и конечную координаты тел в этот промежуток времени:

Теперь посмотрим, чем отличаются графики. Ну так, навскидку. Они отличаются наклоном.

График движения второго тела расположен к оси Х значительно ближе. Что это значит?

Рассмотрим, какое расстояние прошло первое тело, обозначим его на рисунке. Оно численно равно проекции перемещения, убедимся с помощью формулы:

Теперь рассмотрим расстояние, которое преодолело второе тело:

Видим, что за одинаковый промежуток времени второе тело прошло значительно большее расстояние! Это значит, что его скорость больше.

Чем ближе к оси Х расположена прямая, тем больше скорость движения тела.

А что будешь делать с таким графиком?

Координата тела с течением времени не меняется. Значит ли это, что тело не движется вовсе?

Нет. Тело не движется лишь по этой оси. Но по какой-нибудь другой оси оно двигаться может.

Например, вот так:

Тело не меняет координаты по оси Х, однако движется по оси Y.

Если мы видим такой график, мы можем лишь утверждать, что проекция скорости равна нулю. О самой скорости говорить не можем.

Встреча

Помнишь самый первый рисунок с двумя телами? Вот этот:

В нем есть одна интересная деталь. Графики движения тел пересекаются.

Со временем все понятно: оно для всех идет одинаково, ничего не поделаешь.

А вот с координатой интереснее: ведь мы можем утверждать, что в какой-то момент тела встретились. То есть в какой-то момент их координаты на оси Х стали равны. Обозначим момент встречи и координату («место») встречи:

Встреча – такое событие, при котором координаты тел в один и тот же момент времени совпадают.

Это еще один момент, о котором стоит помнить при решении задач на графики.

А еще стоит обратить внимание на то, что координаты тел должны совпадать в один момент времени! Если в лесу мимо дуба пробежала лань, а через несколько дней мимо этого же дуба пробежал енот, мы не можем сказать, что они встретились.

Просто у них совпала траектория.

График зависимости проекции скорости от времени. Нахождение проекции перемещения

Рассмотрим несколько другой график. График зависимости проекции скорости от времени при равномерном прямоли…

Стоп, чего? Какой зависимости? Скорость ведь постоянная и не меняется со временем.

Ты абсолютно прав. А график-то начертить можем, вот так:

Скучный график. Просто прямая, параллельная оси времени. Проекция скорости не меняется, а время всё идет и идет.

Давай хоть что-то найдем по графику. Хоть площадь под ним. Обозначим эту область:

Получили прямоугольник. Его площадь ищем путем перемножения двух соседних сторон, то есть мы берем проекцию скорости и умножаем еще на время.

Где-то мы это слышали.

Верно, ведь именно так ищется проекция перемещения!

Совпадение? Не думаю.

Искать проекцию перемещения таким способом можно не только для равномерного прямолинейного движения, но и для других его видов!

Проекция перемещения тела численно равна площади под графиком скорости тела.

Видео:9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

Решение простейших задач и задач на графики равномерного прямолинейного движения

Текстовые задачи

Задача 1. Охарактеризуйте движение соседки, которая спускается по лестнице и одновременно с этим закатывает рукава, услышав в 11 часов вечера громкую музыку из квартиры снизу, если уравнение ее движения: (x=2cdot t), а ось направлена вниз по лестнице.

Решение:

Итак, для начала вспомним уравнение движения в общем виде:

Соответствует ли уравнение движения соседки уравнению выше? Конечно!

Почему? По глазам вижу, догадываешься! Потому что его можно записать так:

Начальная координата соседки равна нулю: соседка двигалась из начала координат. С этим разобрались. Осталось определить тип ее движения.

Она движется вниз по лестнице. Значит, идет по прямой в одном направлении. Это прямолинейное движение.

Она свирепеет и ускоряется? Нет. Она движется равномерно. Давай вспомним уравнение движения для равномерного прямолинейного движения:

И еще раз посмотрим на наше:

Сопоставляем их и понимаем, что рядом с временем расположена проекция скорости. Она, как видим, положительна и равна 2 м/с. Соседка двигается вдоль оси. Ось направлена вниз и соседка движется туда же!

Подробно мы разбирали зависимость направления от знака проекции в Большой теории по векторам.

Таким образом, соседка совершает равномерное прямолинейное движение вдоль оси из начала координат, а проекция ее скорости на эту ось равняется 2 м/с.

Задача 2. Таракан Вася совершает равномерное прямолинейное движение вдоль линейки (соответствующей оси Х) на столе семиклассника Вовы, который, старательно уча уроки, уже неделю не выносит из комнаты мусор. Проекция скорости таракана на эту ось 0.1 м/с. Вова берет секундомер и начинает отсчет в тот момент, когда таракан находится на втором сантиметре линейки.

На каком сантиметре линейки окажется таракан через две секунды?

Решение:

Первое правило решающих физику: увидеть тему и писать формулы по теме.

Второе правило решающих физику: увидеть тему и писать ВСЕ формулы по теме. Могут пригодиться.

Знаем тип движения! Равномерное прямолинейное!

Знаем уравнение равномерного прямолинейного движения! Пишем:

Делов-то! Начнем подставлять известные величины для таракана. Из задачи знаем, что в начале отсчета таракан находится на втором сантиметре линейки…

Никогда не теряй бдительность, боец. Всегда проверяй величины.

Переведем все, что есть, в СИ. Скорость – в м/с. Отлично, уже есть. Как быть с линейкой? Просто перевести сантиметры в метры!

Таракан был на втором сантиметре, а значит на 0.02 метре линейки!

Теперь можем записать уравнение его движения:

Чтобы узнать, где окажется таракан через 2 секунды, просто подставим цифру 2 в это уравнение:

На 0.22 метре линейки! Получили ответ. Но в задаче спрашивается, на каком сантиметре будет находится таракан. Переводим наш ответ в сантиметры и получаем, что таракан будет находится на 22-ом сантиметре линейки!

Задача 3. По коридору мчится восьмиклассник Петя, уравнение его движения можно описать следующим уравнением: (x=6+2cdot t). За ним несётся разъяренный директор Максим Михайлович, уравнение его движения: (x=3+3cdot t).

Догонит ли директор Петю и, если догонит, когда и на каком метре коридора это произойдет? Скорость измерять в м/с, время в секундах.

Решение:

Итак, давай разберемся. Что вообще значит «догонит»? То же самое, что «встретит», верно?

Мы знаем, что такое встреча. Это такое событие, при котором координаты тел в один и тот же момент времени совпадают.

Чтобы понять, встретятся ли они вообще, давай построим графики движения Пети (П) и директора (Д):

Видим, что прямые пересекаются. В какой-то момент времени их координаты действительно одинаковы.

Но как узнать, в какой?

Что-что? Видно по графику? Ну уж нет! Думаешь, там координата 12? А вдруг там 11.999?

Всегда нужно проверять себя аналитически.

Запишем два уравнения:

(<_>=3+3cdot t) — директора

При встрече у них одинаковые координаты: (<_

>=<_>)

Да… Наверное, другие части уравнений приравнять будет полезнее:

(6+2cdot t=3+3cdot t)

Отсюда легко вычислить время встречи:

Значит, через три секунды после начала отсчета их координаты будут одинаковы, они встретятся. Найдем место встречи, просто подставив время в одно из двух (какое больше нравится 🙂 ) уравнений:

Директор догонит Петю через 3 секунды. Это произойдет на 12-ти метрах от начала коридора.

Задачи на графики

Задача 4. Написать уравнение движение тела, если график этого движения:

Решение:

Какое это движение? Видим, что графиком движения является прямая. Значит, это равномерное прямолинейное движение.

Удивительно, но начнем с уравнения:

График очень информативный. По крайней мере мы уже знаем начальную координату: (<_>=8) м

Как найти проекцию скорости? Ну, давай ее выразим для начала.

Дальше все очень просто: сделаем так, чтобы она осталось единственной неизвестной. Подставим в уравнение координату и время из графика, абсолютно любую пару, вот так:

Проекция скорости отрицательна. И правда: с течением времени тело приближается к началу координат, то есть движется против оси.

Подставим в уравнение:

(x=8-t) — уравнение движения тела.

Задача 5. Тело движется вдоль оси Х. Описать движение на каждом участке графика. Найти проекции скоростей. Построить графики проекции скорости и пройденного пути от времени.

Решение:

Опишем движение. Какое оно?

«Ха! Это не прямая, — скажешь ты, — а ломаная!»

И будешь абсолютно прав.

А я скажу: «А что такое ломаная? Это просто соединенные между собой отрезки! А отрезки — части прямых!»

Поэтому давай рассматривать этот график частями!

С первым отрезком все понятно: равномерное прямолинейное движения, ведь эта часть графика – прямая. С течением времени тело приближается к началу координат, значит движется против оси.

Найдем проекцию скорости.

Для начала, что есть скорость?

Мы помним, что скорость – отношение перемещения к промежутку времени.

Знаем, что это справедливо и для проекций:

Ну, время у нас есть. А проекцию перемещения откуда взять?

Давай вспомним, что это такое. Перемещение – вектор, проведенный из начального положения тела в конечное. А проекция перемещения – проекция этого вектора. Логично, правда? То есть:

Подробнее о проекциях можно узнать в Большой теории по векторам.

Вот и нашли проекцию скорости:

Подставим в уравнение выше значения необходимых величин:

Проекция скорости на первом участке графика равна -3м/с.

Второй отрезок необычнее: тело не меняет координату. Тело на этом участке неподвижно.

Так как в условии сказано, что тело движется именно вдоль оси Х, модуль проекции скорости на эту ось равен длине вектора скорости.

Так как тело не меняет координату, проекция его перемещения равна нулю. А значит и проекция скорости равна нулю.

Третий отрезок описывает равномерное прямолинейное движение. Тело отдаляется от начала координат и движется туда же, куда направлена ось.

Найдем проекцию скорости на третьем участке:

Так. Давай разберемся, почему там 12-7.

Помнишь, мы считаем отношение проекции перемещения к ПРОМЕЖУТКУ времени. А от 7 до 12 секунды промежуток времени составляет 5 секунд.

Проекция скорости на третьем участке равна 1м/с.

Всё нашли, осталось лишь построить графики! Начнем с графика зависимости проекции скорости от времени. Начертим и обозначим оси, обязательно обозначив единицы измерения и помня, что проекция может быть отрицательна:

Работаем с первой частью:

Мы выяснили, что в течение первых двух секунд проекция скорости была постоянна (как-никак, равномерное прямолинейное движение 🙂 ) и равна -3 м/с.

На втором участке проекция скорости равна нулю, а на третьем – единице.

Избавимся от вспомогательных линий и получим:

Что-то мне подсказывает, что на графике пути тоже будет три участка. Приступим.

Нарисуем оси и обозначим их:

Логично будет утверждать, что, пока тело не начало двигаться, оно и путь никакой не прошло. Отметим это точкой на графике:

Первые две секунды тело двигалось равномерно со скоростью 3 метра в секунду. Значит, за две секунды тело прошло (3cdot 2=6) метров! Отметим это. Нет, не так, на графике отметим:

Движемся дальше. Мы знаем, что на втором участке тело было неподвижно, а значит путь никакой не проходило. За промежуток времени второго участка тело не прошло никакой путь.

Однако суммарно за всё свое движение тело все так же прошло 6 метров:

На третьем участке тело движется. Значит, суммарно пройденный путь увеличится. Оно двигалось со скоростью 1м/с. Посмотрим сколько оно прошло за 5 (12-7) секунд.

Оно пройдет 5 метров.

Добавим их к нашим уже пройденным 6 метрам и получим 11 метров:

Остается только соединить точки прямой:

Задача 6. Найти проекцию перемещения тела по графику

Решение:

Определимся, из чего вообще складывается то, что нам нужно найти. В разные промежутки времени тело двигалось с разными постоянными скоростями.

Значит, проекция перемещения складывается из проекций перемещения в разных промежутках времени! Их 6:

Попробуем найти первую проекцию. Помнишь, мы знаем, что проекция перемещения есть площадь под графиком?

«Под графиком» означает «между графиком и осью», то есть вот эта:

Что ж, давай найдем перемещение:

Проекция скорости есть -2м/с, а промежуток времени – 3с.

Попробуем найти площадь второго прямоугольника:

Сразу обрати внимание на то, что промежуток времени – с третьей по пятую секунду, то есть 2 секунды!

Аналогично для остальных:

Посмотрим, чему равна проекция перемещения:

Тяжело в учении – легко в бою. Давай поднажмём и составим график зависимости проекции перемещения от времени.

Когда мы включили таймер, она была равна нулю:

В конце первого промежутка времени она становится равна -6м:

А, ну дальше-то все легко: отмечаем 4, потом отмечаем 9… Нет!

Мы ведь работаем с ОБЩЕЙ проекцией. А общая проекция есть сумма.

Тогда в конце второго промежутка проекция будет равна:

Дальше – больше слагаемых.

Следующая точка: (-6+4=-2) м

А после нее:(-6+4+9=7) м и т.д.

Теперь соединяем точки по порядку:

Задача 7. Постройте траекторию движения колибри, если начальное положение его по оси Х – 1 м, по оси Y – 3 м, а проекция его скорости на оси, расположенные перпендикулярно друг другу, описывается следующими графиками:

Решение:

Увидел сложную задачу – пиши всё, что знаешь! Зачем? Так надо! Пиши!

Скорость изменяется скачками, но на отдельных промежутках она постоянна. Тело движется равномерно.

Тело изменяет свое положение в пространстве. Изменяет свою координату.

Вспомним, как записывается уравнение координаты тела при равномерном прямолинейном движении:

Мы учились делать это раньше. Построим графики зависимости координаты от времени.

Итак, по оси Х у нас 3 участка, обозначим их вспомогательными линиями на нашем новом графике:

Начнем с первого участка. Знаем проекцию скорости и даже начальную координату! Подарок судьбы.

Строим его на первом промежутке:

Теперь координата тела – 17м и тело начинает двигаться с другой скоростью. Из координаты 17 тело движется со скоростью… А, ни с какой скоростью. Проекция скорости на эту ось равна нулю, поэтому:

Координата не меняется. Рисуем:

Тело на 17 м. Оттуда продолжаем движение с проекцией скорости -2 м/с. Тогда: (x=17-2cdot t)

Аналогично строим график для оси Y. Теперь у нас есть два графика:

Построим траекторию движения в плоскости. Для этого нам нужны оси Х и Y одновременно!

Давай построим их:

Всегда бери длину с запасом! Чтобы потом не перечерчивать оси. Наибольшее значение по Х – 17м. По Y – 15м. На всякий случай будем брать 20Х20.

Давай будем анализировать по секундам. Каковы были координаты тела в момент начала отсчета? Давай посмотрим.

В начальный момент времени координата по Х равна 1м, по Y – 3м. В конечный момент по Х координата равна 13, по Y – 15м.

Отметим эти точки:

Дальше будем рассматривать «переломные моменты». Для первого графика это 8 и 10с, для второго – 4 и 6с.

То есть секунды: 4, 6, 8, 10.

Запишем координаты точек для нужных нам секунд:

Отметим их и соединим прямой, укажем последовательность:

Теперь ты знаешь, как работать с графиками равномерного прямолинейного движения и их уравнениями! Движемся дальше. Иронично звучит 🙂

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Средняя скорость по перемещению. Средняя путевая скорость

Хочешь, покажу фокус?

Из горной пещеры вылетает дракон, а за ним в ту же секунду выбегает доблестный рыцарь. Дракон хочет разрушить замок, находящийся от пещеры на расстоянии 7 километров. Задача рыцаря – добраться до замка первым и остановить дракона.

Рыцарь скачет на лошади прямо к замку по равнине в течении 20 минут. Он обнаруживает, что мост через реку на пути к замку разрушен, поэтому решает переплыть реку, и (спасибо его хорошей подготовке) у него уходит лишь 5 минут на то, чтобы снять с себя доспехи и сделать это. Затем в течении 10 минут он продолжает движение к замку.

Дракон после вылета из пещеры движется вперед и вверх, на это у него уходит 15 минут. На какой-то высоте он останавливается, потому что видит стаю пролетающих мимо уток. Драконы, динозавры, птицы… Смекаешь, да? Он решает поиграться со своими «родственниками», на что у него уходит 15 минут. Затем он вспоминает о замке и стремительно пикирует к нему на протяжении 5 минут.

Давай всё это изобразим для наглядности:

Дракон и рыцарь совершили одинаковые перемещения, так? 7 км, ведь они оказались у замка, двигаясь из пещеры.

Давай посчитаем время каждого в пути. И для дракона, и для рыцаря оно составило 35 минут. Они прибыли к замку одновременно.

Так что ж получается… Они совершили одинаковое перемещение за одинаковый промежуток времени.

Но их траектории были очень различны! И двигались они по-разному!

Для того, чтобы описать это, существует средняя скорость по перемещению.

Средняя скорость тела – векторная физическая величина, равная отношению перемещения тела на определенном участке траектории ко времени, за которое оно совершено.

Средняя скорость дракона и рыцаря по перемещению одинакова, ведь они пришли одновременно в одно и то же место.

Есть подвох, о котором тебе на математике не рассказали. Ты все время работал не с этой средней скоростью. А с этой:

Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Понял, да? Путевая – про путь, а не про перемещение. Средняя путевая скорость совпадает (по модулю) со средней скоростью по перемещению только в том случае, если тело двигалось по прямой в одном направлении.

Средняя путевая скорость дракона сильно отличается от средней путевой скорости рыцаря.

Если не помнишь, в чем отличие пути от перемещения, советую посмотреть основные определения кинематики!

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Относительность движения. Операции над скоростями

Давай вспомним одну из важнейших вещей, когда мы говорим про движение. Мы давали ему определение, когда говорили о кинематике в целом.

Это тело отсчета. То тело, относительно которого мы рассматриваем движение.

Мы уже знаем, что относительно одного тела тело может нестись с бешеной скоростью, а относительно другого не двигаться вовсе.

От системы отсчета зависит изменение положения тела. А что еще от нее зависит? Траектория зависит?

Однажды человек изобрел колесо и изменил мир. Давай воспользуемся этим изобретением для того, чтобы найти ответ на вопрос выше.

Возьмем какую-то точку на колесе и пусть оно катится по дороге! Как движется эта точка относительно оси колеса? По кругу.

А относительно Земли?

Эта кривая называется циклоида. И она точно отличается от траектории движения точки относительно оси колеса.

Сегодня мы научимся определять и связывать скорости в разных системах отсчета.

А еще на относительности основан главный закон скоростей – закон об их сложении.

Поступим как настоящие ученые. Готовые формулы – для слабаков. Мы будем выводить их сами.

По реке плывет плот (П) со спортсменом (С). На берегу реки сидит рыбак (Р) и наблюдает за этим. В какой-то момент пловец прыгает с плота и движется к другому берегу реки. Их несёт течение реки.

Давай изобразим это:

Давай нарисуем вектор перемещения спортсмена относительно плота и назовем его относительным перемещением:

Теперь нарисуем вектор перемещения плота, которого несет течение. Назовем этот вектор переносным:

А теперь посмотрим, как спортсмен двигался относительно рыбака, и назовем вектор этого перемещения абсолютным:

Ты только посмотри! У нас тут треугольник!

Нет, оставь свои теории заговора и иллюминатов. Не тот треугольник. Треугольник суммы векторов!

Переносное перемещение и относительное в сумме дают абсолютное!

Как связать перемещение со скоростью? Нужно поделить его на время!

🎥 Видео

Урок 15. Решение задач на графики движенияСкачать

Выполнялка 168. Равноускоренное движение. Как строить графики.Скачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

Графики зависимости скорости и расстояния от времени. Физика 7 класс.Скачать

На рисунке приведён график зависимости проекции Vx скорости тела от времени t - №22677Скачать