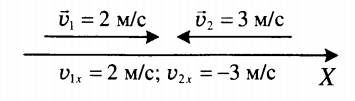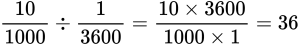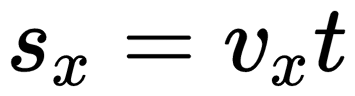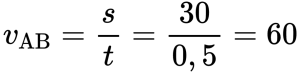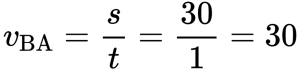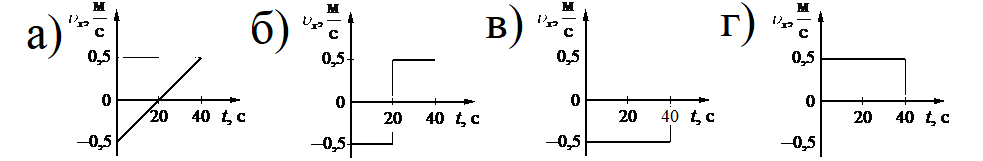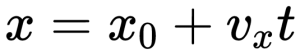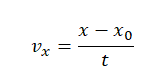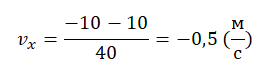Уравнение зависимости проекции на ось скорости движущегося тела от времени

Видео:Графики зависимости пути и скорости от времениСкачать

Уравнение зависимости проекции на ось скорости движущегося тела от времени

3.1. Равнопеременное движение по прямой.

3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением:

3.1.2. Ускорение () — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.

В векторном виде:

где — начальная скорость тела, — скорость тела в момент времени t.

В проекции на ось Ox:

где — проекция начальной скорости на ось Ox, — проекция скорости тела на ось Ox в момент времени t.

Знаки проекций зависят от направления векторов и оси Ox.

3.1.3. График проекции ускорения от времени.

При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.):

Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения

3.1.4. Скорость при равнопеременном движении.

В векторном виде:

В проекции на ось Ox:

Для равноускоренного движения:

Для равнозамедленного движения:

3.1.5. График проекции скорости в зависимости от времени.

График проекции скорости от времени — прямая линия.

Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox.

Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; где — изменение скорости за время

Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).

3.1.6. Геометрический смысл площади под графиком в осях

Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом.

На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции:

(3.9)

3.1.7. Формулы для расчета пути

(3.10)

(3.12)

(3.11)

(3.13)

(3.14)

Все формулы, представленные в таблице, работают только при сохранении направления движения, то есть до пересечения прямой с осью времени на графике зависимости проекции скорости от времени.

Если же пересечение произошло, то движение проще разбить на два этапа:

до пересечения (торможение):

После пересечения (разгон, движение в обратную сторону)

В формулах выше — время от начала движения до пересечения с осью времени (время до остановки), — путь, который прошло тело от начала движения до пересечения с осью времени, — время, прошедшее с момента пересечения оси времени до данного момента t, — путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t, — модуль вектора перемещения за все время движения, L — путь, пройденный телом за все время движения.

3.1.8. Перемещение за -ую секунду.

За время тело пройдет путь:

За время тело пройдет путь:

Тогда за -ый промежуток тело пройдет путь:

За промежуток можно принимать любой отрезок времени. Чаще всего с.

Если то

Тогда за 1-ую секунду тело проходит путь:

Если внимательно посмотрим, то увидим, что и т. д.

Таким образом, приходим к формуле:

Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорением движется тело. Подчеркнем, что это соотношение справедливо при

3.1.9. Уравнение координаты тела при равнопеременном движении

Знаки проекций начальной скорости и ускорения зависят от взаимного расположения соответствующих векторов и оси Ox.

Для решения задач к уравнению необходимо добавлять уравнение изменения проекции скорости на ось:

3.2. Графики кинематических величин при прямолинейном движении

3.3. Свободное падение тела

Под свободным падением подразумевается следующая физическая модель:

1) Падение происходит под действием силы тяжести:

2) Сопротивление воздуха отсутствует (в задачах иногда пишут «сопротивлением воздуха пренебречь»);

3) Все тела, независимо от массы падают с одинаковым ускорением (иногда добавляют — «независимо от формы тела», но мы рассматриваем движение только материальной точки, поэтому форма тела уже не учитывается);

4) Ускорение свободного падения направлено строго вниз и на поверхности Земли равно (в задачах часто принимаем для удобства подсчетов);

3.3.1. Уравнения движения в проекции на ось Oy

В отличии от движения по горизонтальной прямой, когда далеко не всех задач происходит смена направления движения, при свободном падении лучше всего сразу пользоваться уравнениями, записанными в проекциях на ось Oy.

Уравнение координаты тела:

Уравнение проекции скорости:

Как правило, в задачах удобно выбрать ось Oy следующим образом:

Ось Oy направлена вертикально вверх;

Начало координат совпадает с уровнем Земли или самой нижней точкой траектории.

При таком выборе уравнения и перепишутся в следующем виде:

3.4. Движение в плоскости Oxy.

Мы рассмотрели движение тела с ускорением вдоль прямой. Однако этим равнопеременное движение не ограничивается. Например, тело, брошенное под углом к горизонту. В таких задачах необходимо учитывать движение сразу по двум осям:

Или в векторном виде:

И изменение проекции скорости на обе оси:

3.5. Применение понятия производной и интеграла

Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.

где A, B и то есть постоянные величины.

Теперь посмотрим, как понятие производной и интеграла применимо к физическим величинам. В математике производная обозначается «’», в физике производная по времени обозначается «∙» над функцией.

то есть скорость является производной от радиус-вектора.

Для проекции скорости:

то есть ускорение является производной от скорости.

Для проекции ускорения:

Таким образом, если известен закон движения то легко можем найти и скорость и ускорение тела.

Теперь воспользуемся понятием интеграла.

то есть, скорость можно найти как интеграл по времени от ускорения.

то есть, радиус-вектор можно найти, взяв интеграл от функции скорости.

Таким образом, если известна функция то легко можем найти и скорость, и закон движения тела.

Константы в формулах определяются из начальных условий — значения и в момент времени

3.6. Треугольник скоростей и треугольник перемещений

3.6.1. Треугольник скоростей

В векторном виде при постоянном ускорении закон изменения скорости имеет вид (3.5):

Эта формула означает, что вектор равен векторной сумме векторов и Векторную сумму всегда можно изобразить на рисунке (см. рис.).

В каждой задаче, в зависимости от условий, треугольник скоростей будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

3.6.2. Треугольник перемещений

В векторном виде закон движения при постоянном ускорении имеет вид:

При решении задачи можно выбирать систему отсчета наиболее удобным образом, поэтому не теряя общности, можем выбрать систему отсчета так, что то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда

то есть вектор равен векторной сумме векторов и Изобразим на рисунке (см. рис.).

Как и в предыдущем случае в зависимости от условий треугольник перемещений будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Графики равноускоренного движения

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На прошлом уроке мы изучили основные законы и зависимости равноускоренного движения. На этом уроке мы научимся строить графики равноускоренного движения – это графики зависимости проекции скорости от времени, графики зависимости проекции перемещения от времени, графики зависимости координаты от времени, и анализировать эти графики. Также решим несколько типовых задач по этой теме.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

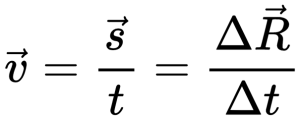
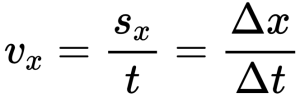
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Дополнительные единицы измерения

• 1 км/ч (километр в час) = 1000 м/3600 с.
• 1 км/мин (километр в минуту) = 1000 м/60 с.
• 1 км/с (километр в секунду) = 1000 м/с.
• 1 м/мин (метр в минуту) = 1 м/60 с.
• 1 см/с (сантиметр в секунду) = 0,01 м/с.

Спидометр — прибор для измерения модули скорости тела.

График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Определение направления движения по графику скорости

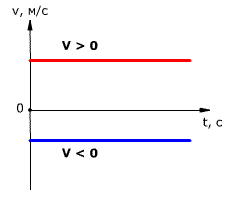
• Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
• Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
• Если график скорости совпадает с осью времени, тело покоится.

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

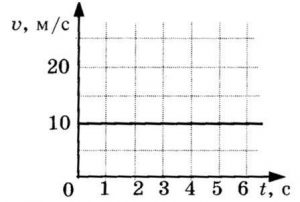
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

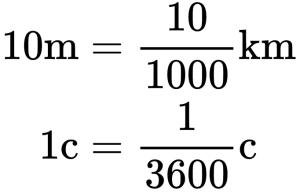
Видео:7 класс, 6 урок, Графики зависимости пути и скорости от времениСкачать

Перемещение и координаты тела при равномерном прямолинейном движении

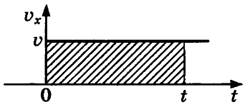
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

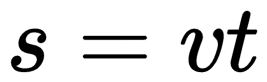
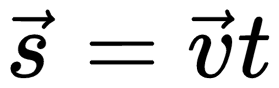
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Определение направления движения по графику проекции перемещения

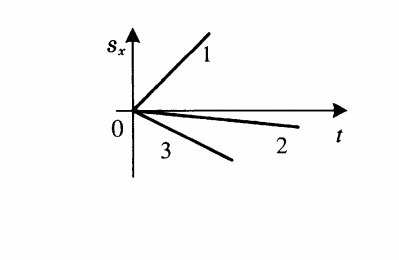
• Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
• Если луч лежит ниже оси времени, тело движется против оси ОХ.
• Если луч совпадает с этой осью, тело покоится.

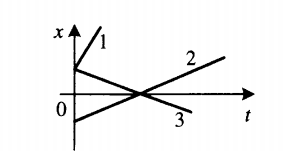
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Определение направления движения тела по графику координаты

• Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
• Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
• Если координата не изменяется, тело покоится.

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

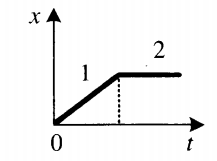
Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

1. На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
2. Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
3. На участке 1 тело движется равномерно, а на участке 2 оно покоится.
4. На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
5. Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

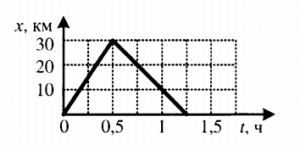
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

1. Выбрать любой временной интервал.
2. Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
3. Записать формулу скорости и вычислить ее для 1 и 2 тела.
4. Найти n — отношение скорости второго тела к скорости первого тела

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

• Для графика 1: начальный путь s₁₀ = 0 м. Конечный путь равен s₁ = 80 м.
• Для графика 2: начальный путь s₂₀ = 0 м. Конечный путь равен s₂ = 120 м.

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Какой из графиков соответствует зависимости от времени для проекции υ x скорости этого тела на ось Ox ?

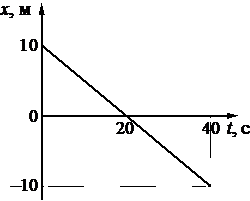
Алгоритм решения

1. Записать уравнение координаты при равномерном прямолинейном движении.
2. Выразить из уравнения проекцию скорости.
3. Определить начальную и конечную координаты, а также время, в течение которого двигалось тело.
4. Вычислить проекцию скорости.
5. Выбрать соответствующий график.

Решение

Уравнение координаты при равномерном прямолинейном движении имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

💥 Видео

Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

На рисунке приведён график зависимости проекции Vx скорости тела от времени t - №22677Скачать

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Физика 7 кл (2013 г) Пер §17 Упр 4 №4 . График зависимости скорости равномерного движения тела от врСкачать

Проекция перемещения на ось XСкачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Урок 3 Определение координаты движущегося телаСкачать

Решение графических задач на равномерное движениеСкачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

Определение координаты движущегося тела. Видеоурок по физике 9 классСкачать

Построение проекции вектора на осьСкачать

§3 Физика 9кл. Определение координаты движущегося телаСкачать

На графике приведена зависимость скорости прямолинейно движущегося тела от времени - №22656Скачать