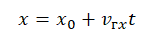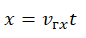- теория по физике 🧲 кинематика
- Совместное движение двух тел
- Графики прямолинейного движения
- Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
- Скорость не меняется — движение равномерное
- Равномерное движение в направлении противоположном оси
- Равноускоренное движение в направлении оси, скорость увеличивается
- Равноускоренное движение против оси
- Скорость уменьшается — движение равнозамедленное
- Равнозамедленное движение против оси
- Выводы
- Применение координатного и графического способов описания прямолинейного равномерного движения при решении задач кинематики
- Ход урока
- 1. Подготовка к активной деятельности на основном этапе занятия
- Построение алгоритма решения задачи.
- 💥 Видео
теория по физике 🧲 кинематика
Уравнение координаты — зависимость координаты тела от времени:
Уравнение координаты при равноускоренном прямолинейном движении:
x0 — координата тела в начальный момент времени, v0x —проекция начальной скорости на ось ОХ, ax —проекция ускорения на ось ОХ, x — координата тела в момент времени t
Зная уравнение координаты, можно определить координату тела в любой момент времени.
Пример №1. Движение автомобиля задано уравнением:
Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x0 = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v0 = 0 м/с.
В момент времени t = 10 c координата автомобиля равна:
Видео:Графики зависимости пути и скорости от времениСкачать

Совместное движение двух тел
Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.
Аналитический способ решения задачи на совместное движение тел
Чтобы найти место встречи двух тел, нужно:
- Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
- Построить уравнение вида x1 = x2.
- Найти время встречи двух тел tвстр.
- Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату xвстрч.
Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.
Составим уравнения для движения каждого из тел:
Приравняем правые части этих уравнений и найдем время t:
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:
x = 3t = 3∙6 = 18 (м).
Графический способ решения задачи на совместное движение тел
Существует графический способ решения данной задачи. Для этого нужно:
- Построить графики x1(t) и x2(t).
- Найти точку пересечения графиков.
- Пустить перпендикуляр из этой точки к оси ОХ.
- Значение точки пересечения — координата места пересечения двух тел.
Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.
Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!
Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием tзапазд, то его уравнение координаты принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.
Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).
В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:
Приравняем правые части уравнений и вычислим t:
В результате получаем два
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.
В момент времени t=0 проекции её скорости υx и ускорения ax на ось Ох удовлетворяют соотношениям:
а)
б)
в)
г)
Алгоритм решения
- Определить характер движения материальной точки.
- Записать уравнение координаты материальной точки.
- С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.
Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 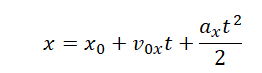
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Записать исходные данные.
- Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
- Выразить скорость грузовика из уравнения его движения.
- Записать уравнение движения мотоциклиста.
- Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
- Подставить время в формулу скорости грузовика и вычислить ее.
Решение
- Координата встречи грузовика и мотоциклиста: x = 150 м.
- Время запаздывания мотоциклиста: tзапазд = 5 с.
- Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .
Запишем уравнение движения грузовика:
Так как начальная координата равна нулю, это уравнение примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда скорость движения грузовика равна:
Запишем уравнение движения мотоциклиста:
Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:
Найдем время, через которое грузовик и мотоциклист встретились:
Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:7 класс, 6 урок, Графики зависимости пути и скорости от времениСкачать

Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_ + v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_ + a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec) и (vec) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Видео:Физика: зависимость координаты тела от времениСкачать

Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Видео:Решение графических задач на равномерное движениеСкачать

Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
Видео:9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

Применение координатного и графического способов описания прямолинейного равномерного движения при решении задач кинематики
Разделы: Физика
Учебная: научить суворовцев решать задачи кинематики.
Методическая:
- получить алгоритм перехода от координатного способа описания прямолинейного равномерного движения к графическому при решении задач;
- решение задач;
- показ приема использования данной темы в военном деле.
Развивающая:
- развитие речи, памяти;
- логического мышления, внимания, воображения;
- развитие умения анализировать и самостоятельно формулировать выводы.
Воспитательная:
- воспитание аккуратности и точности при построении графиков движения;
- воспитание трудолюбия, ответственного отношения к учебе, любви к профессии военного.
Материальное обеспечение: кодоскоп, телевизор, видеомагнитофон, экран, видеокассета.
Связь с другими предметами: математика, начальная военная подготовка.
Тип урока: урок решения задач.
Метод работы: алгоритмический.
Продолжительность урока: 45 мин.
| Этапы урока | Время |
| 1. Организация начала занятий. | 1 мин. |
| 2. Проверка выполнения самоподготовки – фронтальная беседа. | 5 мин. |
| 3. Подготовка к активной деятельности на основном этапе занятия, объявление темы и цели занятия. | 2 мин. |
| 4. Усвоение новых знаний. Построение алгоритма решения задачи. | 20 мин. |
| 5. Первичная проверка понимания суворовцами нового учебного материала. (Проводится на протяжении изучения темы урока). | 3 мин. |
| 6. Закрепление знаний. Решение задачи по построенному алгоритму. | 5-6 мин. |
| 7. Обобщение и систематизация знаний. | 2 мин. |
| 8. Контроль и самопроверка знаний. | 3 мин. |
| 9. Подведение итогов занятия. | 1-2 мин. |
| 10. Информация о задании на самоподготовку, инструктаж по его выполнению. | 1-2 мин. |
Видео:Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Ход урока
1. Подготовка к активной деятельности на основном этапе занятия
На предыдущих уроках мы познакомились с двумя способами описания прямолинейного равномерного движения – координатным и графическим. Они связаны между собой, так как описывают одно и то же движение. Если задан один из способов описания, например, координатный, то по заданному уравнению можно построить и график зависимости координаты и проекции скорости от времени. Существует и обратная возможность записи уравнения движения по известным графикам зависимости координаты и проекции скорости от времени.
Взаимосвязь между различными способами описания прямолинейного равномерного движения можно изобразить на следующей схеме.
(Показать на экране с помощью кодоскопа рисунок 1).
Рисунок 1
Сегодняшний урок мы посвятим определению порядка действий и операций при переходе от координатного к графическому способу описания прямолинейного равномерного движения на примере следующей задачи:
Движение тела описывается уравнением х = 2 + 3t, где все величины даны в СИ. Найти начальную координату тела, проекцию скорости тела на ось ОХ. Построить графики зависимостей координаты тела и проекции его скорости от времени.
Построение алгоритма решения задачи.
Учитель. В начале решения задачи необходимо провести поиск признаков, по которым можно определить объект, описанный в условии, и раздел физики, в котором изучается данный объект.
Ключевым словом в условии задачи является слово движение. Движение тел изучается физической теорией, которая называется механикой, поэтому наличие этого слова в условии сразу указывает на теорию, которую нужно применить для решения.
В условии дано уравнение зависимости координаты тела от времени. Эти уравнения для различных видов движений, изучаются в разделе механики, который называется кинематикой.
Учитель. Охарактеризуйте зависимость х = 2 + 3t.
Ученик. Уравнение зависимости координаты от времени показывает, что между координатой и временем существует прямопропорциональная зависимость, поэтому движение тела является прямолинейным и равномерным.
(С помощью кодоскопа на экране высвечивается лист повторения).
1. Прямолинейным равномерным движением называют такое движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения.
2. Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка:

3. Перемещение при прямолинейном равномерном движении 
4. Зависимость координаты x от времени t:
5. Проекция скорости на координатную ось равна изменению координаты в единицу времени и изображена на рисунках 2 и 3:
 |  |
| Рис. 2 | Рис. 3 |
6. Графики движения (рисунок 4).
7. Графики скорости (рисунок 5).
 |  |
| Рис. 4 | Рис. 5 |
“Движение” 
Уравнение зависимости координаты от времени 
Прямопропорциональная зависимость координаты от времени 

2. Действия и операции при поиске начальной координаты и проекции скорости по уравнению зависимости координаты от времени.
Учитель. Для нахождения начальной координаты и проекции скорости тела нужно сопоставить общее уравнение координаты прямолинейного равномерного движения с частным уравнением, заданным в условии задачи. Запишем эти уравнения в виде системы для удобства их сравнения.
В частном уравнении физические величины должны иметь тот же смысл, что, и в общем.
Вопрос. Какой смысл имеют цифры 2 и 3 в частном уравнении?
Ученик. Цифра “2” в частном уравнении имеет смысл начальной координаты тела, выраженной в метрах: хо = 2 м.
Множитель, стоящий перед t имеет смысл проекции скорости, поэтому для данного частного случая Vx = 3 м/c.
Учитель. Что означает знак “+” перед проекцией скорости?
Ученик. Перед проекцией скорости стоит знак “+”; поэтому скорость тела сонаправлена с осью ОХ.
Учитель. Таким образом, мы определили первое действие и операции в алгоритме решения задач такого типа. (Спроектировать на экран с помощью кодоскопа действие 1).
Действие 1. Сопоставить общую и частную формы записи уравнения зависимости координаты от времени:
- свободный член в частной форме записи уравнений дает начальную координату тела хо;
- численный коэффициент, стоящий перед временем t в линейном члене в частной форме записи уравнения, задает величину проекции скорости;
- знак величины, стоящий перед временем t, определяет направление скорости по отношению к выбранной системе координат.
3. Действия и операции при построении графика зависимости координаты от времени по известному уравнению данной зависимости.
Учитель. Построим график зависимости координаты тела от времени движения х = 2 + 3t. Для этого вспомним соответствующий раздел алгебры.
Ученик. Мы знаем, что график представляет собой прямую линию. Для построения прямой необходимо задать две любые ее точки. Точки выбираются произвольно, но для простоты расчетов одну из них свяжем с начальным моментом времени t = 0. Тогда из уравнения х = 2 + 3t следует, что хо = 2м (х = 2м + 3м/с · 0 = 2м). Т.к. это координата в начальный момент времени, то ее следует обозначить хо. Пусть t = 2с, тогда х = 8м.
| t,с | 0 | 2 |
| х,м | 2 | 8 |
Учитель. Таким образом, мы выполнили второе действие алгоритма решения задачи. (Спроектировать на экран с помощью кодоскопа действие 2).
Действие 2. Рассчитать координаты двух точек графика с помощью частного уравнения зависимости х(t) путем подстановки в него двух различных моментов времени, один из которых принимается равным нулю.
Предложить суворовцу изобразить график зависимости х(t) на доске, комментируя все свои действия.
Ученик. Изобразим оси координат. Вертикальная ось соответствует координате, измеренной в метрах, горизонтальная ось времени — в секундах. Выберем удобный масштаб осей координат. Отметим полученные точки А(0;2) и В(2;8) на координатной плоскости и проведем через них прямую.
Учитель. Итак, мы выполнили еще три последовательных действия алгоритма. (Спроектировать на экран с помощью кодоскопа действия 3, 4 и 5).
Действие 3. Изобразить оси координат и выбрать масштаб изображения координаты и времени согласно рисунку 6.
 | ||
| Рис. 6 | Рис. 7 | Рис. 8 |
Действие 4. Изобразить на графике расчетные точки (см. рис. 7).
Действие 5. Провести через отмеченные точки прямую, которая и будет являться графиком зависимости координаты от времени (см. рис. 8).
4. Действия и операции при построении графика зависимости проекции скорости от времени.
Учитель. Построим график зависимости проекции скорости от времени. В действии 1, при сопоставлении общей и частной форм записи уравнений движения было определено, что проекция скорости Vх равна 3, а также знак проекции.
Вопрос. Что будет являться графиком Vх = 3 в координатных осях Vх, t?
Ученик. Графиком будет являться прямая, параллельная оси времени.
Учитель предлагает суворовцу выйти к доске и изобразить график зависимости Vх от t, комментируя все свои действия.
Изобразим оси координат для построения графика. Вертикальная ось соответствует проекции скорости, измеренной в метрах в секунду, горизонтальная ось – времени, измеренному в секундах. Выберем масштаб оси координат. На оси проекции скорости найдем точку Vх = 3 с учетом ее знаков. Так как проекция скорости остается постоянной, то любым другим моментом времени будет соответствовать та же проекция скорости, поэтому график будет представлять собой прямую, параллельную оси времени. Это известное свойство графика функции, не зависящей от ее аргумента. Проведем прямую, параллельную оси времени через точку Vх = 3.
Учитель. Определен следующий порядок действий. Посмотрите на экран. (Спроектировать на экран с помощью кодоскопа действие 6, 7, 8).
Действие 6. Изобразить оси координат и выбрать масштаб изображения проекции скорости и времени (см. рис. 9).
 | ||
| Рис. 9 | Рис. 10 | Рис. 11 |
Действие 7. Изобразить на вертикальной оси точку, соответствующую проекции скорости с учетом ее знака (см. рис. 10).
Действие 8. Провести через точку на вертикальной оси соответствующую величине и знаку проекции скорости прямую, параллельную оси времени (см. рис. 11).
Учитель. Итак, мы получили порядок действий при построении графиков движения и скорости для прямолинейного равномерного движения по известному уравнению зависимости координаты от времени. Многие из этих действий в дальнейшем будут выполняться автоматически, в уме, так как они довольно просты. И время решения задачи заметно сократится.
Учитель. Пользуясь разобранным примером решения задачи, ответьте на вопросы и выполните указанные действия при решении задачи на карточках. (Каждый ученик имеет следующую карточку).
Задание выполнял ученик _________________________________ класс _____
Условия задачи. Зависимость координаты движущегося тела от времени выражается уравнением вида х = 6 – 2t. Найдите начальную координату и проекцию скорости движения данного тела, постройте графики зависимостей координаты и проекции скорости от времени.
1. По каким признакам, указанным в условии задачи, можно определить, что в условии описано прямолинейное равномерное движение?
2. Какое действие нужно совершить для нахождения начальной координаты и проекции скорости движения?
3. Выполните действие, названное в п.2; и определите начальную координату, величину и знак проекции скорости
4. Перечислите действия, которые необходимо выполнить для построения графика зависимости координаты тела от времени
5. Выполните действия, названные в п.4; и постройте график зависимости координаты от времени.
6. Перечислите действия, которые необходимо выполнить для построения графика зависимости проекции скорости тела от времени.
7. Выполните действия, указанные в п.6; и постройте график зависимости проекции скорости от времени.
Обобщение и систематизация знаний
Учитель. На сегодняшнем уроке мы показали алгоритм перехода от координатного способа описания к графическому. На первый взгляд он может показаться очень громоздким. На самом деле в результате многократного применения действий и операций по совместному применению координатного и графического методов эти действия как бы сворачиваются, переходят в умственный план, совершаются в подсознании. На поверхности остается результат в виде уравнения и графиков движения и скорости. Это и есть высший уровень овладения умениями решать задачи по данной теме.
Подведение итогов занятия, выставление оценок
Задание на самоподготовку. Построить аналогичным образом алгоритм перехода от графического способа описания к координатному на примере задачи:
На рисунке 12 изображен график зависимости координаты движущегося тела от времени. Найдите проекцию скорости тела, запишите уравнение зависимости координаты тела от времени и постройте график зависимости проекции скорости от времени.
💥 Видео
Урок 15. Решение задач на графики движенияСкачать

Равномерное движение: график зависимости координаты от времениСкачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

Выполнялка 53.Гармонические колебания.Скачать

Физика - уравнения равноускоренного движенияСкачать

Уравнение движенияСкачать

Уравнение координат при равноускоренном движенииСкачать

Равноускоренное движение: график зависимости координаты и скорости от времениСкачать

Выполнялка 168. Равноускоренное движение. Как строить графики.Скачать

Равнозамедленное движение: график зависимости координаты и скорости от времениСкачать