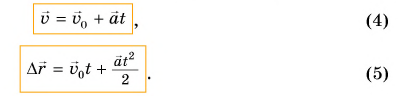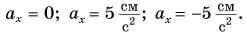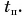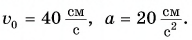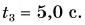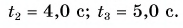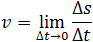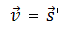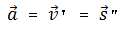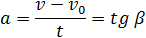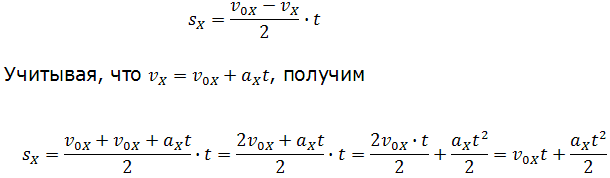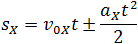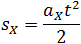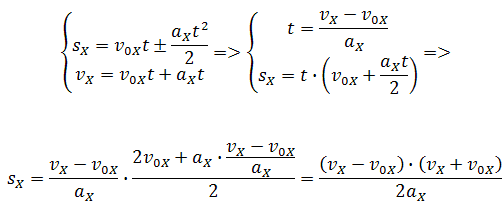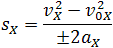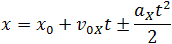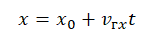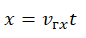Уравнение зависимости координаты от времени для равнопеременного движения (7 видео)

Перемещение, координата и путь при равнопеременном движении в физике с примерами

Перемещение, координата и путь при равнопеременном движении:

Мы знаем, что при равнопеременном движении скорость тела линейно зависит от времени. А как зависит от времени перемещение? Координата? Пройденный путь?

В предыдущем параграфе для равнопеременного движения была найдена зависимость проекции скорости от времени:

и получена формула для проекции перемещения:

Подставляя 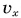из равенства (1) в (2), находим зависимость проекции перемещения от времени:

Отметим, что при движении с постоянным ускорением соотношения (1) и (3) выполняются и для векторов скорости и перемещения:

Учитывая, что проекция перемещения 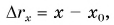из формулы (3) находим координату:

Формула (6) выражает кинематический закон равнопеременного движения. Функции (3) и (6) называются квадратичными. Следовательно, при равнопеременном движении проекция перемещения тела и его координата квадратично зависят от времени.

Сравним зависимости основных кинематических величин от времени для двух видов прямолинейного движения: равномерного и равнопеременного (табл. 1).

Таблица 1

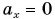
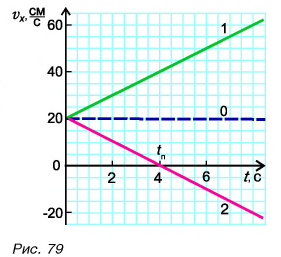
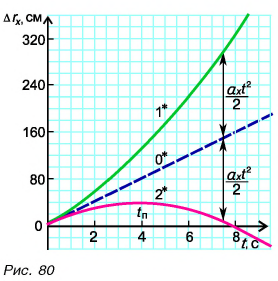
Из таблицы видно, что при формулы равнопеременного движения переходят в формулы равномерного.

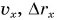
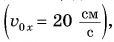
Рассмотрим графики проекций и координаты х на конкретном примере: три тела (0, 1 и 2) движутся вдоль оси Ох. Их начальные скорости одинаковы проекции ускорения различны:

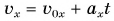
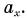
По формуле (1) построим графики проекции скорости этих тел (графики 0, 1, 2 на рис. 79). Графики прямолинейны, а их наклон определяется значением проекции ускорения График 2 пересекает ось времени в момент поворота

Перейдем к графикам проекции перемещения 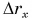(рис. 80).

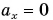
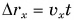
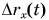
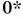
Как мы знаем, при (т. е. для равномерного движения) и график — наклонная прямая линия (график на рис. 80).

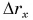
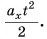
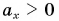
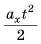
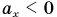
Из таблицы 1 видно, что формулы для проекции перемещения при равномерном и равнопеременном движениях отличаются только на слагаемое Поэтому при точки графика 0* для каждого значения t следует поднять на (график 1*), а при (график 2*) — настолько же опустить (рис. 80).

Так как 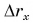квадратично зависит от времени (см. формулу (3)), графики проекции перемещения при равнопеременном движении являются участками парабол (рис. 80).

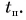
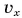
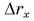
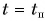
Обратите внимание на поведение графиков 2 и 2* в момент поворота График 2 для (рис. 79) в этот момент проходит через нуль, а график 2* для (рис. 80) при достигает максимума, а затем начинает опускаться. Графики подтверждают: в момент поворота направление движения тела изменяется на противоположное.

А каким будет график пути? Для движения, при котором направление скорости не изменяется, график пути 1б (рис. 81) совпадает с графиком проекции перемещения 1а. Если же скорость меняет свое направление, то график пути s (2б) и график проекции перемещения 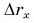(2а) будут совпадать лишь до момента поворота

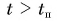
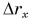
При проекция перемещения начинает уменьшаться, а путь s продолжает расти. Он увеличивается на столько, на сколько за то же время уменьшается проекция перемещения.

От графика проекции перемещения 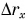легко перейти к графику координаты х (рис. 82).

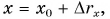
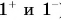
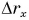
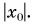
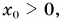
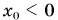
Так как, согласно формуле (6), то графики координаты х (параболы ) получаются путем смещения графика на величину Смещение вверх происходит при а вниз — при (рис. 82). Выведем еще две формулы, полезные для решения задач о равнопеременном движении.

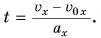
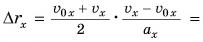
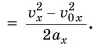
Выразим время из формулы проекции скорости (1): Подставив это выражение в формулу (2), получим:
Следовательно, при равнопеременном движении

В случае когда начальная скорость и ускорение одинаково направлены, из равенства (7) следует:

где s — пройденный путь.

Главные выводы:

При равнопеременном движении тела его перемещение и координата — квадратичные функции времени.
Графики зависимости проекции перемещения и координаты от времени для равнопеременного движения являются участками парабол.
Вершина параболы на графике проекции перемещения соответствует моменту времени, при котором мгновенная скорость равна нулю.

Пример решения задачи:

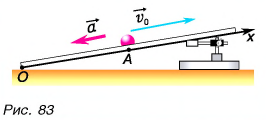
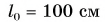
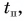
Шарику, находящемуся в точке А, расположенной посередине наклонного желоба длиной (рис. 83), сообщили начальную скорость вдоль наклонного желоба вверх. Ускорение шарика направлено вдоль желоба вниз. Найдите координату точки поворота и время за которое шарик ее достигнет, если

Определите время, когда шарик вернется в точку А, и время, когда он окажется в точке О. Постройте графики проекций скорости и перемещения, а также координаты шарика.

Пример решения задачи:

Решение

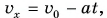
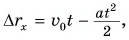
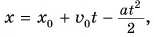
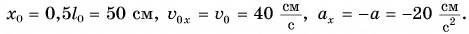
Выберем ось Ох, как показано на рисунке 83. Тогда проекция скорости проекция перемещения координата где
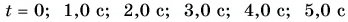
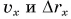
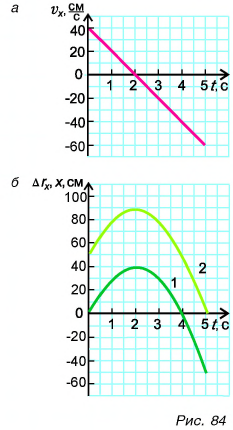
По этим формулам для моментов времени найдем значения и занесем результаты в таблицу.

Используя полученные значения, строим графики проекций скорости (рис. 84, а) и перемещения (рис. 84, б, график 1) за промежуток времени от 0 до 5 с.

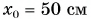
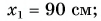
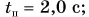
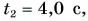
График координаты получим, сдвинув график проекции перемещения на вверх (график 2 на рис. 84, б). Из графиков и таблицы находим: координата точки поворота шарик достиг ее в момент в точке А шарик оказался при а в точке О — при

Ответ: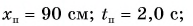

Рекомендую подробно изучить предметы:

Физика
Атомная физика
Ядерная физика
Квантовая физика
Молекулярная физика

Ещё лекции с примерами решения и объяснением:

Криволинейное движение
Ускорение точки при ее движении по окружности
Инерциальные системы отсчета
Энергия в физике
Прямолинейное равноускоренное движение
Сложение скоростей
Ускорение в физике
Скорость при равнопеременном движении

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Содержание

Равнопеременное прямолинейное движение
Уравнение координаты при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Совместное движение двух тел
🌟 Видео

Видео:Графики зависимости пути и скорости от времениСкачать

Равнопеременное прямолинейное движение

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

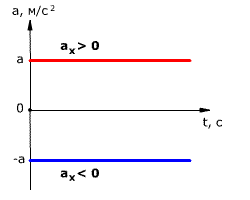
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

Проекция вектора скорости на ось ОХ:

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

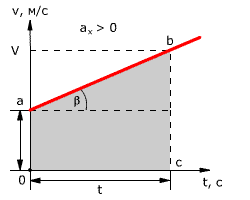
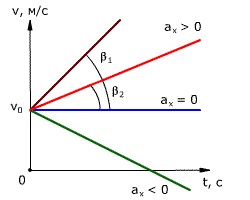
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

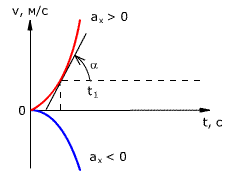
Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

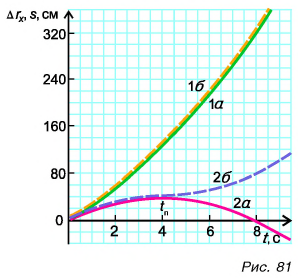
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x

Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Видео:Физика: зависимость координаты тела от времениСкачать

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
Построить уравнение вида x₁ = x₂.
Найти время встречи двух тел t_встр.
Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Построить графики x1(t) и x2(t).
Найти точку пересечения графиков.
Пустить перпендикуляр из этой точки к оси ОХ.
Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

Определить характер движения материальной точки.
Записать уравнение координаты материальной точки.
С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Записать исходные данные.
Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
Выразить скорость грузовика из уравнения его движения.
Записать уравнение движения мотоциклиста.
Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
Подставить время в формулу скорости грузовика и вычислить ее.

Решение