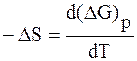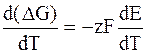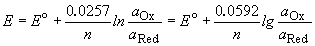Электрохимический метод широко применяется при исследовании термодинамических свойств различных химических процессов, на основе которых можно построить равновесные электрохимические цепи.
Кроме того, этот метод более прост, а также позволяет изучать процессы при высоких температурах, что свидетельствует о ряде преимуществ перед другими.
Измерение ЭДС позволяет определить такие термодинамические характеристики, как изобарный потенциал (DG), тепловой эффект реакции (DН), изменение энтропии (DS) и константу равновесия (Кр) окислительно-восстановительной реакции, которая протекает в гальваническом элементе.
Определение термодинамических характеристик
Токообразующей реакции
Токообразующей реакцией называется та окислительно-восстановительная реакция, которая самопроизвольно протекает в гальваническом элементе.
Например, в элементе Даниэля –Якоби:

|
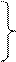


Zn 0+ + Cu 2+ ® Zn 2+ + Cu 0 токообразующая реакция
C помощью электрохимического метода могут быть рассчитаны следующие термодинамические характеристики:
а) Расчет изменения потенциала (DG).
Из раздела термодинамики известно, что
Для электрохимической цепи максимальную электрическую работу характеризует величина
где z – количество электронов, принимающих участие в реакции;
F – число Фарадея.
Следовательно, DG = zFE (7.78)
Это уравнение служит основой расчета DG различных химических реакций. Часто электрохимический метод определения изобарного потенциала имеет существенные преимущества передтермохимическим методом.
б) Расчет константы равновесия (Кр).
При стандартных условиях
Из термодинамики также известно, что
Следовательно, 
Величина Кр характеризует полноту протекания химической реакции и вычисляется из уравнения:

в) Расчет изменения энтропии (DS).
Из раздела термодинамики известно, что
Используя уравнение (7.6.1)
находим, что
Следовательно, 
где 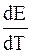
изменяется ЭДС при изменении температуры на 1 градус.
Для нахождения 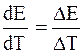
ЭДС гальванической цепи зависит от температуры. Для одних цепей она увеличивается с повышением температуры, а для других – уменьшается. Изучение температурной зависимости гальванической цепи представляет большой интерес. Точное измерение самой ЭДС и ее температурного коэффициента 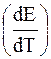
г) Расчет теплового эффекта реакции (DH).
К гальванической цепи, как и ко всякой химической и электрохимической системе, находящейся при постоянном давлении применимы все основные уравнения химической термодинамики, в том числе и уравнения Гиббса – Гельмгольца:
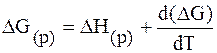
где DH – изменение энтальпии в ходе химической реакции.
Используя уравнения (7.6.1) и (7.6.3), получим
–z FE = DH – Tz F
или DH = – z F 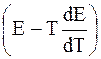
Следовательно, измерив ЭДС и взяв ее производную 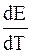
Если все члены уравнения Гиббса – Гельмгольца разделить на zF и поменять знаки, то с учетом формулы
Е = –
получим следующее выражение:
Е = – 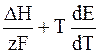
Как уже указывалось ранее

то 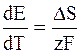
Таким образом, температурный коэффициент характеризует и изменение энтропии (DS) в ходе соответствующей химической реакции, а величина
zFT . 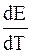
определяет тепловой эффект при обратимом протекании химической реакции в электрохимической системе.
С другой стороны, DH характеризует тепловой эффект химической реакции при ее необратимом протекании в условиях постоянного давления.
Будем рассматривать только самопроизвольно протекающие химические реакции, для которых Е > 0.
Такого вида электрохимические реакции протекают в гальваничес-ких элементах.
На опыте наблюдаются все три случая зависимости ЭДС от температуры
1. 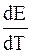
2. 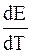
3. 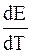
Если 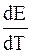
т.е. вся энергия, выделяющаяся при химической реакции, превращается в электрическую работу (W = zFE).
Если 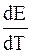
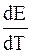
т. е. только часть энергии, выделяющейся при химической реакции, превращается в электрическую работу, а другая часть (q) выделяется в виде теплоты и элемент нагревается.
Наиболее интересен случай, когда 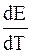
z F E = DH + z F E . 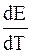
т.е. электрическая работа больше энергии, выделяющейся при химической реакции на величину (q).
Дополнительная работа получается за счет теплоты, которую элемент отбирает от окружающей среды. Если система изолирована, то элемент охлаждается.
Таким образом, не имея разности температур, можно получить превращение теплоты в работу, т.е. протекает отрицательный процесс с уменьшением энтропии.
Электрохимические цепи, отвечающие таким необычным условиям, действительно можно реализовать.
Пример 1.
Рассмотрим следующую цепь:
в которой осуществляется реакция
ЭДС этой цепи при 25 0 С Е = 0,0465, а 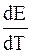
Решение:
По формуле (6.4) найдем изменения энтальпии
» 5,3 . 10 3 Дж/моль = 5,3 кДж/моль
Положительное значение DH указывает на эндотермический характер приведенной реакции. Аналогичные закономерности наблюдаются за счет возрастания энтропии системы.
Пример 2.
Рассчитать значения 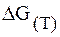
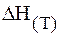
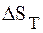
если ее ЭДС равен 0,536 В, а температурный коэффициент равен 0,45 . 10 –4 В/к. Написать уравнение реакции протекающий в цепи.
Решение:
Электрохимическая цепь состоит из двух электродов II рода

реакции: Hg2Cl2 + 2 
токообразующая реакция: Pb + Hg2Cl2 PbCl2 + 2Hg
Используем уравнения (7.78), (7.80) и (7.81) для нахождения 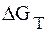
1) 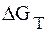
3) DНТ = 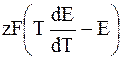
2) DST = 
отрицательное значение ( 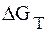
Весьма интересным является вопрос о коэффициенте полезного действия (КПД) при работе элемента (h). Если просто сжигать топливо, а затем превращать часть теплоты в работу тепловой машины, то достигается небольшой КПД (до 0,3-0,4). Если же осуществлять химическую реакцию окисления топлива в электрическом элементе, то можно получить значительно больший КПД.
Теоретически КПД может быть больше единицы в элементах, у которых температурный коэффициент больше нуля, т.е. если 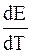

Таким образом, по экспериментальным значениям ЭДС (Е) можно не только определять важнейшие термодинамические характеристики токообразующей реакции, которые будут такими же и в том случае, если данная реакция протекает не в элементе, но и можно решить обратную задачу, т.е. по термодинамическим данным рассчитать ЭДС (Е) и температурный коэффициент. Заметим также, что зная 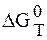
затем по известному значению Е 0 можно вычислить ЭДС для любых концентраций ионов в растворе. Например, для реакции
Е = Е0 – 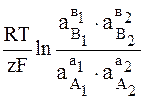
Так, многие стандартные потенциалы металлов, которые не могут быть определены экспериментально, вычислены на основании термодинамичес-ких данных. Например, для щелочных и щелочноземельных металлов, которые бурно реагируют с водой, для алюминия и магния, которые легко покрываются пленкой и т.д.
Видео:Урок 184 (осн). Зависимость сопротивления металлов от температурыСкачать

Определение термодинамических характеристик электрохимических цепей
Лабораторная работа № 1
Определение термодинамических характеристик электрохимических цепей.
Система, состоящая из двух электродов, помещенных в раствор электролита, которая при соединении электродов вне электролита каким-либо металлическим проводником создает во внешней цепи электрический ток, называется гальваническим (или электрохимическим) элементом.
Условная запись (схема) гальванического элемента
Для описания гальванических элементов применяется условная запись, в соответствии с которой сначала указывается материал одного из электродов, далее – раствор, в который помещен этот электрод, затем раствор, в который погружен второй электрод, и, наконец, материал другого электрода. Электроды отделяются от раствора сплошной вертикальной линией, а растворы разделяются либо двумя вертикальными линиями, когда считают, что на границе растворов нет скачка потенциала, либо пунктирной линией, когда таким скачком пренебречь нельзя. Так, медно-цинковый элемент может быть записан следующим образом:
где знаки + и – указывают полярность электродов; c1 и c2 – концентрации растворов.
При большой разнице между c1 и c2, когда нельзя пренебречь скачком потенциала на границе двух растворов, этот элемент записывают в другом виде:
(-)Zn½ZnSO4
В тех же случаях, когда хотят указать только участвующие в электродных реакциях ионы, запись упрощают:
Для обратимо работающего гальванического элемента ток всегда должен идти слева направо, а на концах быть один и тот же металл.
Устройство медно-цинкового гальванического элемента (элемента Даниэля-Якоби) показано на рисунке.
Рисунок — Медно-цинковый элемент (элемент Даниэля-Якоби):
1 – пористая диафрагма; 2 – цилиндрический электрод из листового цинка; 3 – медный электрод.
При замыкании электродов через внешнюю цепь на медном электроде пойдет процесс восстановления меди:
а на цинковом электроде – процесс окисления цинка:
Электроны, остающиеся на электроде при реакции окисления, будут перетекать во внешней цепи от цинка к меди, где будут участвовать в процессе восстановления меди. В растворе при работе гальванического элемента ток будет переноситься ионами меди и цинка, движущимися к цинковому электроду, и сульфат-ионами, движущимися к медному электроду.
Равновесные потенциалы медного и цинкового электродов связаны с активностями ионов меди и цинка в растворе уравнением Нернста:
Электродвижущая сила (ЭДС) гальванического элемента. Стандартная ЭДС
Разность равновесных потенциалов электродов гальванического элемента называется электродвижущей силой этого элемента. Для элемента Даниэля-Якоби это можно выразить:

где 
Стандартная ЭДС обратимо работающего гальванического элемента равна разности стандартных потенциалов отдельных электродов гальванического элемента, причем, так как ЭДС всегда положительная величина, от положительного потенциала отнимается отрицательный потенциал.
Вывод уравнения Нернста для гальванического элемента
Если в электрохимической системе обратимо и изотермически протекает следующая реакция:

при 
и обратимая ЭДС ( ЕP, T) системы определяется как:
В то же время изменение энергия Гиббса реакции определяется формулой:
и так как 
где 
В состоянии равновесия при данных давлении и температуре 
Если активности всех компонентов равны единице (аi=1), то 


где Ка — константа равновесия реакции. Из этого следует, что:
Если аi = 1, то 
где Е0 — стандартная ЭДС. Полученное после подстановки уравнение называется уравнением Нернста:


Обратимые и необратимые гальванические элементы
Гальванические элементы могут быть обратимыми и необратимыми. Гальванический элемент является обратимым, если токообразующая реакция в элементе может быть обращена в противоположном направлении при приложении к нему извне ЭДС, превышающей собственную ЭДС элемента на бесконечно малую величину. Примером обратимых гальванических элементов может служить элемент Даниэля-Якоби (если пренебречь переходом ионов через границу растворов):
В этом элементе при его работе будет иметь место реакция:
Zn + CuSO4 ® Cu + ZnSO4
Если к элементу приложить внешнюю ЭДС, противоположно направленную относительно ЭДС элемента, то в нем будет идти реакция:
Cu + ZnSO4 ® CuSO4+ Zn,
т. е. в отличие от токообразующей реакции в элементе медь начнет растворяться, а цинк – выделяться из раствора.
Примером необратимого элемента может служить цепь:
В этом элементе при его работе будет идти процесс:
Zn + CuSO4 ® ZnSO4+Cu
Если приложить к нему внешнюю противоположно направленную ЭДС, то будет происходить процесс растворения меди на медном электроде и ее выделение на цинковом, т. е. этот процесс не будет обратным процессу при работе такого гальванического элемента.
Термодинамические характеристики гальванического элемента
Работа какого-либо обратимого процесса при определенных ограничениях, налагаемых на условия осуществления процесса, например при постоянстве температуры и давления, будет максимальной полезной работой, поэтому термодинамический расчет ЭДС возможен только в случае обратимых гальванических элементов. Зависимость максимальной полезной работы химической реакции в гальваническом элементе от температуры можно связать с уравнениями Гиббса-Гельмгольца:
Максимальная полезная работа электрохимической реакции равна
Подставляя в уравнения Гиббса-Гельмгольца вместо DG и DF их значения, выраженные через ЭДС, можно получить эти уравнения в форме, связывающей ЭДС с тепловым эффектом реакции и температурой:
где ¶Е/¶T – температурный коэффициент, который показывает во сколько раз изменяется ЭДС при увеличении температуры на 1 К.
Или, учитывая, что — DН=Qp – тепловой эффект реакции при постоянном давлении, а — DU=Qv — тепловой эффект реакции при постоянном объеме, можно получить уравнения Томсона, являющиеся частным случаем уравнений Гиббса-Гельмгольца:
В том случае, когда ЭДС гальванического элемента не зависит от температуры, т. е. (¶Е/¶T)р=0 или (¶Е/¶T)v=0, эти уравнения переходят в:
Если ¶Е/¶T > 0, то 
Видео:Зависимость электрического сопротивления металлов от температуры. Сверхпроводимость. 8 класс.Скачать

Уравнение зависимости эдс от температуры
Для гальванического элемента принята следующая форма записи (на примере элемента Даниэля):
где вертикальная линия | обозначает границу раздела фаз, а двойная вертикальная линия || — солевой мостик. Электрод, на котором происходит окисление, называется анодом; электрод, на котором происходит восстановление, называется катодом. Гальванический элемент принято записывать так, чтобы анод находился слева.
Электродные полуреакции принято записывать как реакции восстановления (таблица 12.1), поэтому общая реакция в гальваническом элементе записывается как разность между реакциями на правом и левом электродах:
Правый электрод: Cu 2+ + 2e = Cu
Левый электрод: Zn 2+ + 2e = Zn
Общая реакция: Cu 2+ + Zn = Cu + Zn 2+
Потенциал E электрода рассчитывается по формуле Нернста:
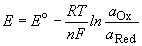
где aOx и aRed — активности окисленной и восстановленной форм вещества, участвующего в полуреакции; E o — стандартный потенциал электрода (при aOx = aRed =1); n — число электронов, участвующих в полуреакции; R — газовая постоянная; T — абсолютная температура; F — постоянная Фарадея. При 25 o C
Стандартные электродные потенциалы электродов измеряются относительно стандартного водородного электрода, потенциал которого принят равным нулю. Значения некоторых стандартных электродных потенциалов приведены в таблице 12.1.
Электродвижущая сила (ЭДС) элемента равна разности потенциалов правого и левого электродов:
Если ЭДС элемента положительна, то реакция (так, как она записана в элементе) протекает самопроизвольно. Если ЭДС отрицательна, то самопроизвольно протекает обратная реакция.
Стандартная ЭДС равна разности стандартных потенциалов:
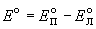
Для элемента Даниэля стандартная ЭДС равна
E o = E o (Cu 2+ /Cu) — E o (Zn 2+ /Zn) = +0.337 — (-0.763) = +1.100 В.
ЭДС элемента связана с 

Зная стандартную ЭДС, можно рассчитать константу равновесия протекающей в элементе реакции:
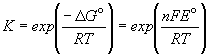
Константа равновесия реакции, протекающей в элементе Даниэля, равна
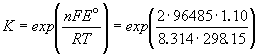
Зная температурный коэффициент ЭДС 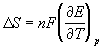




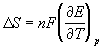
Таблица 12.1. Стандартные электродные потенциалы при 25 o С.
Электрод
Электродная реакция
E o , В
PbSO4 + 2H2O
Пример 12-1. Рассчитать стандартный электродный потенциал пары Cu 2+ /Cu + по данным таблицы 11.1 для пар Cu 2+ /Cu и Cu + /Cu.
Cu 2+ + 2e = Cu 
Cu + + e = Cu 
Cu 2+ + e = Cu + 
откуда E o = +0.153 В.
Пример 12-2. Составить схему гальванического элемента, в котором протекает реакция
Рассчитать стандартную ЭДС элемента при 25 o C, 
Ag | AgBr| Br — || Ag + | Ag
Правый электрод: Ag + + e = Ag E o = 0.7792 В
Левый электрод: AgBr + e = Ag + Br — E o = 0.0732 В
Общая реакция: Ag + + Br — = AgBr E o = 0.7260 В

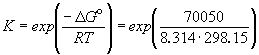
1/K= a(Ag + ) . a(Br — ) = m(Ag + ) . m(Br — ) . ( 
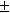

Отсюда, полагая 
Пример 12-3. 

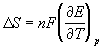



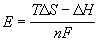
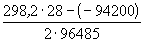
Ответ. 
12-1. Рассчитать стандартный электродный потенциал пары Fe 3+ /Fe по данным таблицы 12.1 для пар Fe 2+ /Fe и Fe 3+ /Fe 2+ . (ответ)
12-2. Рассчитать произведение растворимости и растворимость AgCl в воде при 25 o C по данным таблицы 12.1. (ответ)
12-3. Рассчитать произведение растворимости и растворимость Hg2Cl2 в воде при 25 o C по данным о стандартных электродных потенциалах. (ответ)
12-4. Рассчитать константу равновесия реакции диспропорционирования 2Cu + 
12-5. Рассчитать константу равновесия реакции ZnSO4 + Cd = CdSO4 + Zn при 25 o C по данным о стандартных электродных потенциалах. (ответ)
12-6. ЭДС элемента, в котором обратимо протекает реакция 0.5 Hg2Cl2 + Ag = AgCl + Hg, равна 0.456 В при 298 К и 0.439 В при 293 К. Рассчитать 


12-7. Вычислить тепловой эффект реакции Zn + 2AgCl = ZnCl2 + 2Ag, протекающей в гальваническом элементе при 273 К, если ЭДС элемента E= 1.015 В и температурный коэффициент ЭДС = — 4.02 . 10 -4 В . K -1 . (ответ)
12-8. В гальваническом элементе при температуре 298 К обратимо протекает реакция Cd + 2AgCl = CdCl2 + 2Ag. Рассчитать изменение энтропии реакции, если стандартная ЭДС элемента E o = 0.6753 В, а стандартные энтальпии образования CdCl2 и AgCl равны -389.7 и -126.9 кДж . моль -1 соответственно. (ответ)
12-9. ЭДС элемента Pt | H2 | HCl | AgCl | Ag при 25 o C равна 0.322 В. Чему равен pH раствора HCl . (ответ)
12-10. Растворимость Cu3(PO4)2 в воде при 25 o C равна 1.6 . 10 -8 моль . кг -1 . Рассчитать ЭДС элемента Pt | H2 | HCl (pH = 0) | Cu3(PO4)2 (насыщ. р-р) | Cu при 25 o C. (ответ)
12-11. Три гальванических элемента имеют стандартную ЭДС соответственно 0.01, 0.1 и 1.0 В при 25 o C. Рассчитать константы равновесия реакций, протекающих в этих элементах, если количество электронов для каждой реакции n = 1. (ответ)
12-12. ЭДС элемента Pt | H2 | HBr | AgBr | Ag в широком интервале температур описывается уравнением: E o (В) = 0.07131 — 4.99 . 10 -4 (T — 298) — 3.45 . 10 -6 (T — 298) 2 . Рассчитать 


12-13. Для измерения pH раствора можно применять хингидронный электрод. (Хингидрон, Q . QH2, представляет собой комплекс хинона, Q = C6H4O2, и гидрохинона, QH2 = C6H4O2H2). Электродная полуреакция записывается как Q + 2H + + 2e 
12-14. В гальваническом элементе обратимо протекает реакция CuSO4 + Zn = ZnSO4 + Cu. Рассчитать 

12-15. В элементе Вестона протекает реакция Cd + Hg2SO4 = Cd 2+ + 2Hg. Рассчитать ЭДС этого элемента при 303 K, если 

12-16. 


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
🎥 Видео
Зависимость эл-кого сопротивления металлов от температуры. Сверхпроводимость. Практ. часть. 8 класс.Скачать

Зависимость сопротивления от температурыСкачать

Гальванические элементы. 1 часть. 10 класс.Скачать

Влияние температуры на скорость химических реакций. 10 класс.Скачать

Зависимость сопротивления металлов от температурыСкачать

Зависимость электрического сопротивления от температурыСкачать

Зависимость скорости реакции от температуры. Химический опытСкачать

Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Уравнение Нернста. Условия изменения направления ОВР. Продукты в ОВР. Ч.5-3.Скачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Кипение, удельная теплота парообразования. 8 класс.Скачать

ПЛОТНОСТЬ воздуха в зависимости от ТЕМПЕРАТУРЫСкачать

Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать
Уравнение состояния идеального газа. 10 класс.Скачать

Использование таблиц потенциалов и расчет ЭДС реакции. Продукты в ОВР. Ч.5-1.Скачать

Уравнение НернстаСкачать
Температура и тепловое равновесие. Определение температуры | Физика 10 класс #30 | ИнфоурокСкачать

Химическое равновесие. Константа равновесия. 10 класс.Скачать