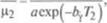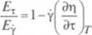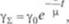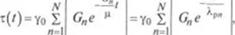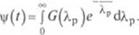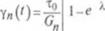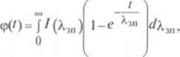Уравнение зависимость вязкости от температуры

Видео:График зависимости плотности воды от температурыСкачать

Зависимость вязкости от температуры

С повышением температуры вязкость капельных жидкостей и их смесей понижается.

Математических уравнений, пригодных для практического применения, выражающих закон изменения вязкости от температуры, до настоящего времени не имеется, поэтому пользуются эмпирическими зависимостями. Для минеральных масел с вязкостью > 80 ccm при температурах от 30 до 150 0 С пользуются выражением

где и – кинематические коэффициенты вязкости при заданной температуре t и температуре 50 0 С в ccm;

n – показатель степени, значения которого в зависимости от исходной вязкости при 50 0 С приведены ниже.

Вязкость	2,8	6,25	9,0	11,8	21,2	29,3
Показатель n	1,39	1,59	1,72	1,79	1,99	2,13
Вязкость	37,3	45,1	52,9	60,6	68,4	80,0
Показатель n	2,24	2,32	2,42	2,49	2,52	2,56

В гидросистемах применяются жидкости, вязкость которых при 50 0 С составляет 10-100 спз. В частности вязкость применяемого в самолетных гидросистемах масла АМГ – 10 при 50 0 С равна 10 ccm.

Зависимость вязкости распространенных масел от температуры показана на рис. 2. а и б. Очевидно, чем меньше изменяется вязкость с изменением температуры, тем выше качество и лучше эксплуатационные свойства рабочей жидкости. При применении жидкостей, имеющих крутую кривую температурной зависимости вязкости, затруднена работа гидросистемы в зимних условиях эксплуатации.

Обычно вязкостно – температурные свойства жидкостей характеризуются отношением Жидкость, предназначенная для эксплуатации в широком температурном интервале, считается пригодной, если ее вязкость при изменении температуры от – 50 0 С до + 50 0 С изменяется не более, чем в 100 раз.

Рис. 2. Графики зависимости динамической вязкости

масел от температуры:

1 – трансформаторное; 2 – индустриальное 12;

3- индустриальное 20; 4 – индустриальное 30;

Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Эмпирические уравнения зависимости вязкости от температуры

Интерполяционные формулы и уравнения с двумя постоянными. Предложено значительное число эмпирических формул, связывающих вязкость жидкостей с их температурой (см. обзоры М. М. Кусакова и К. С. Рамайя , там же приводится подробная библиография). Наиболее простые из них представляют собой обычные интерполяционные формулы или их варианты, принятые при подборе эмпирических формул. К их числу относятся формула Пуазейля:

Постоянные величины, входящие в эти формулы (а, 0, С), не имеют физического смысла. Близки к таким формулам уравнения температурной зависимости текучести, предложенные Бинга-мом.

Однако эта формула имеет весьма ограниченное применение. Более широко применяется основная формула Бингама с тремя константами

Для воды, спиртов и других жидкостей, содержащих гидро-ксильную группу, формула (IV, 9) неприменима. Лучшие результаты дает эмпирическое уравнение Бингама с четырьмя постоянными:

Уравнения этого типа будут передавать вязкостно-температурную зависимость тем точнее, чем больше в них постоянных величин. Однако возрастание числа постоянных усложняет их применение, так как количество экспериментальных измерений, которые нужно производить для вычисления постоянных, не меньше их числа. Для применения формул (IV, б, 7 и 9) необходимо измерять вязкость по крайней мере при трех температурах.

Эмпирические формулы с двумя постоянными обычно передают с достаточным приближением зависимость вязкости от температуры простых нормальных жидкостей.

Для многих нормальных жидкостей, а также для некоторых не слишком вязких аномальных жидкостей, применимы эмпирические соотношения типа формулы Слотта:

которая была проверена на 70 жидкостях (преимущественно нормальных), исследованных Торпом и Роджером.

Недавно А. И. Бачинский отметил, что формула

предложенная им для смазочных масел. Согласно этой формуле необходимо приписать одинаковый наклон кривой rj = /(/) для всех минеральных масел, что совершенно не соответствует действительности. Неудачна также использованная в некоторых английских работах формула Дарси :

так как она отражает линейную зависимость 1/rj от /, что не имеет места в сколько-нибудь широком интервале температур.

Значительный интерес представляет группа эмпирических уравнений, разработанная для выражения вязкостно-температурной зависимости нефтепродуктов, расплавленных стекол и аналогичных по своим механическим свойствам аномальных жидкостей.

Сравнительно давно И. Д. Афанасьев на обширном экспериментальном материале (автолы, вапоры и т. д.) показал, что многие масла в координатах grjt — Igt дают прямые или кривые, близкие к прямым. Степенная или экспоненциальная зависимость вязкости от температуры лежит в основе всех эмпирических формул рассматриваемого типа. Для расплавленных стекол, у которых вязкость очень сильно зависит от температуры, Ле-Шателье предложил формулу

где е—основание натуральных логарифмов; Т—абсолютная температура; а и С константы. В логарифмической форме уравнение (IV, 16) имеет вид

П. П. Лазарев , а также Б. В. Дерягин и И. Я. Хананов нашли, что более хорошие результаты можно получить, если ввести в эту формулу еще одну постоянную щ:

можно вычислить из соотношения

а по оси ординат —

температура t. Тогда постоянная А будет равна отрезку на оси ординат, отсекаемому прямой, построенной на основании уравнения (IV, 18), а постоянная В будет равна тангенсу угла наклона этой прямой.

Близко к уравнению Ле-Шателье первое уравнение К. С. Ра-майя , предложенное для нефтепродуктов

Оно отличается от уравнений (IV, 16) коэфициентом А и тем, что а для всех жидкостей становится постоянным и равным двум.

Широкое распространение в смазочном деле получило уравнение Вальтера, которое также является вариантом уравнения Ле-Шателье, В экспоненциальной форме оно имеет вид

где v выражено в сантистоксах.

Дважды логарифмируя это уравнение, получим

Вводя обозначение g g к = Л и С = В, получаем обычную логарифмическую форму уравнения Вальтера:

На графике в координатах g g (100 vt + 0,8) или g g (vt + + 0,8) и g T для многих нефтепродуктов получаются прямые линии.

Широкое применение уравнения Вальтера связано с тем, что на его основе построены простые номограммы для вычисления вязкости масел и других нефтепродуктов при различных температурах.

Измерив вязкость при двух достаточно далеко отстоящих одна от другой температурах, нанеся на номограмму g g (?х + 0,8), lg lg (v2 + О8) lg7 и ]g T2 и проведя через полученные точки прямую, можно найти vt при заданной Т.

Однако это уравнение имеет существенные недостатки. Его постоянные, как и постоянные всякой другой чисто эмпирической формулы, лишены физического смысла. Логарифмирование приводит к сглаживанию вязкостно-температурной зависимости, а двойное логарифмирование в еще большей степени выравнивает реальную вязкостно-температурную зависимость. По этой причине наклоны прямых

Для жидких нефтепродуктов, сильно разнящихся по своим вязкостно-температурным свойствам, мало отличаются один от другого. С другой стороны, постоянная величина В, характеризующая наклон, в действительности не является постоянной для данного образца масла и зависит от точек, взятых для расчета. Это уравнение является лишь известным приближением, полезным в тех случаях, когда нужно быстро вычислить величину вязкости по двум измерениям, даже допуская при этом значительную ошибку. В последнее время обнаружено, что некоторые масла вообще не подчиняются уравнению Вальтера , особенно при температурах ниже 20—40° . М. П. Воларович рекомендует брать вязкость для вычисления по номограмме уравнения Вальтера не при 50° и 100° или 38,2° и 98е, как это делалось раньше, а при нуле и 100°, что несколько улучшает применимость уравнения.

Некоторые весьма полезные вязкостно-температурные уравнения представляют собой теоретические уравнения в которые введены дополнительные эмпирические постоянные. В таком виде эти уравнения становятся применимыми и ко многим аномальным жидкостям. В частности, к ним относятся формулы, связанные с уравнением Рамана:

В этом уравнении А равно величине, к которой стремится вязкость ?? при увеличении температуры; обычно она называется вязкостью при бесконечной температуре. Величина В имеет смысл энергии активации течения . Это уравнение вполне приемлемо для маловязких жидкостей, но непригодно для таких, как минеральные масла и вязкие нефтепродукты. Б. В. Дерягин и М. М. Кусаков показали, что, введя в уравнение третью постоянную и несколько преобразовав его по сравнению с (IV, 21), можно придти к уравнениям

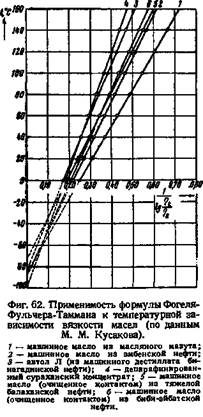
дающим хорошие результаты для смазочных масел. Уравнение (IV, 22) известно под названием формулы Фогеля-Фульчера-Таммана. Фульчер с успехом применял его для расплавленных стекол, а Тамман—для переохлажденных жидкостей.

Согласно М. М. Кусакову постоянные этого уравнения щ, В и /с имеют более или менее отчетливый физический смысл. Постоянная ??0 является вязкостью при бесконечно большой температуре, В показывает, насколько уменьшается вязкость с повышением температуры. Формально она равна числу градусов, на которые нужно нагреть жидкость, чтобы ее вязкость была в 10 раз больше 70, наконец, величина /> является температурой, при которой вязкость обращается в бесконечность, т. е. температурой г при которой жидкость застывает. Следует, однако, отметить, что температура бесконечной вязкости не совпадает с температурой застывания, а величина В недостаточна для характеристики пологости вязкостно-температурной кривой.

Подобно постоянным других уравнений постоянные уравнения Фогеля-Фульчера-Таммана могут быть определены аналитическим или графическим путем.

, и подстановка

приводят к следующим зависимостям:

Как видно из этих формул, аналитическое вычисление постоянных щ, В и too связано с довольно сложными расчетами. Для практических целей достаточно пользоваться менее точным, но более простым графическим способом их определения . Формулу (IV, 23) можно переписать в следующем виде:

откуда следует, что температура / является линейной функцией

температурные значения у и t дают прямую линию. Тангенс угла наклона этой прямой будет равен В, а отрезок, отсекаемый ею на оси /, будет равен /то. Применимость рассматриваемого уравнения к смазочным маслам подтверждается данными М. М. Кусакова (фиг. 62). Трудная задача номографирования уравнения Фогеля-Фульчера Таммана была недавно успешно решена Г. В. Виноградовым.

или в логарифмической форме

зависимость вязкости от температуры изображается прямой. Вычисление постоянных уравнений (IV, 23) настолько просто, что не нуждается в объяснении.

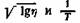
С помощью собственных измерений и путем обработки многочисленных литературных данных К. С. Рамайя подтвердил применимость своей формулы к смазочным маслам и другим нефтепродуктам в широком интервале температур (фиг. 63). Формула дает лучшие результаты для вязких жидкостей и неприменима для бензина и низших углеводородов. Для этих жидкостей подходит неизмененная формула Рамана.

обычно имеют один, редко два перелома. Температура перелома у различных жидкостей неодинакова. Во многих случаях с повышением вязкости жидкости она смещается в сторону высоких температур. Однако Г. И. Фукс и Н. Г. Пучков показали, что если повышать вязкость масел растворением в нем присадок, то точка перелома не меняется . Таким образом, она зависит от состава жидкости, а не только от вязкости.

К. С. Рамайя объясняет изменение наклона

как

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

ЗАВИСИМОСТЬ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ

Хорошо известно, что температура оказывает значительное влияние на реологические свойства материалов. Это утверждение особенно справедливо дтя высоко полимеров. В данном разделе рассматривается влияние температуры на вязкость. Предметом

Для частного случая, при п = I, уравнение (1.49) приводит к результату, полученному для ньютоновского течения в приме­ре 1.1.

п. к тшцсго обсужления являются инженерные методы исследова­ния юмпературной зависимости вязкости неньютоновских жид — ■ опей; эта задача особенно важна для процессов переработки но­чи мерой.

ффект представлен на рис. 1.8, где логарифмическая кри­вая Iечения становится прямой и (в виде графической зависимо — in Igpo от 1/7), как и предполагалось, описывается уравнением ). Заметим, что в данном случае точки хорошо ложатся на ч>ямую линию. На рис. 1.9 показаны те же самые данные, пред-

нменные в виде графической зависимости lgp0 от /’, описывае — ||>п. как предполагается, уравнением (1.51). Заметим, что суше­ние г некоторая кривизна линии, проведенной через точки, полу — I иные для полиэтилена, однако в относительно узком интервале

1,8 2,0 2.2 2.4 2,6 2,8

360 400 440 480 520 560

Рис. 1.8. Зависимость ирслсльной ньюго — Рис. 1.9. Зависимость вязкости от аб*

мовской вязкости от обратной абсолют — солютной температуры:

а — полиэтилен низком плотности

а — полиэтилен ниткой плотности: б — (П’)ВД); 6- поливииилбутираль

температур полученные кривые для большинства технических це­лей можно принимать за прямые.

Данные по течению для большинства промышленно важных термопластов собраны Вестовсром |3|. Им была изучена зависи­мость вязкости ti от температуры при постоянной скорости сдвига.

или в эквивалентной форме:

Р1 = р2 ехр[6, (Ъ — Т)] = р2 ехр(й, д Т).

Замети м, что когда ДТ =/Ь.(,

Величина 1/fy показывает, на сколько градусов нужно увели­чить температуру полимера при постоянной скорости сдвига, что­бы вязкость уменьшилась в 1/е раз. Чтобы показать это, запишем выражение (1.51) в виде

Следовательно, смысл значения l/fy раскрыт.

11сньютоновская вязкость г| является функцией деформации t пипа (так как характеризуется значениями у или т), так же как и функцией температуры. Это выражается функциональными урав­нениями:

Следовательно, когда известно изменение п с температурой, представляет интерес исследование изменения вязкости при по — » тинной скорости сдвига или при постоянном напряжении сдви — i. i Вообще, ( имена я температурном нмкрвале 108—230 ’С

Заметим, что при очень малых напряжениях сдвига энергии ак­тивации остаются неизменными. Этот результат можно предска­зать на основании уравнения (1.59) подстановкой частной произ­водной из (1.60):

ЭГ JT RT2’ [drjj RT2

При этом получим выражение

которое показывает, что £т становится равным Гу, когда у стре­мится к нулю. Этот общий результат применим ко всем жидко­стям. Для ньютоновских жидкостей Ех равно Гу при всех услови­ях, так как (Эп/Эт)у. =0.

Вязкоупругими называются жидкости, проявляющие как упру — iiie (упругое восстановление формы), так и вязкие свойства (вяз-

11ч цемента Ньютона

Дифференцируя уравнение (1.65) но времени, получим: dvv dy,, dyN

И $ закона Гука для сдвига (уравнение (1.66)] имеем:

Интегрированием уравнения (1.85) в пределах от у0 до Yx полу­

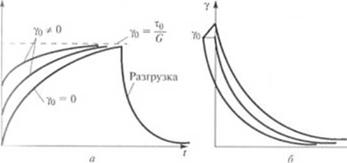
Уравнение (1.87) характеризует изменение величины деформа — ции во времени при постоянном напряжении.

Из этого уравнения следует, что при / = 0, у — уо > а при / = со yv = T0/G, т. с. простая модель Кельвина—Фойгта ведет себя как мЪдель Гука.

Графическая иллюстрация уравнения (1.87) представлена на рис. 1.14.

При разгрузке (мгновенное снятие приложенного напряжения) имеем:

I «ила уравнение (1.87) принимает вил

| io явление называется зопаздывающей да/юрмацией, или упру­гим последействием, а отношение р/6* = /3, имеющее размерность мргмепи, — временем запаздывания.

ОГмзбтенные модели Максвелла и Кельвина—Фойгта, Простые note «и Максвелла и Кельвина—Фойгта не всегда оказываются ик мточными для исчерпывающего описания поведения реаль­ных полимерных материалов. Чтобы распространить данные мо — н hi на более сложные системы, близкие к реальным жидкостям,

• и мыиастся удобным рассматривать ряд простых максвслловс-

• и «цементов, соединенных параллельно, либо в послело ватсль-

!'»• I 14. Графическая иллюстрация повеления просюй модели Кельвина—Фойпа мри |’.i гшчных режимах деформирования:

■сформирование при постоянном напряжении; б — мгновенное снятие напряжения

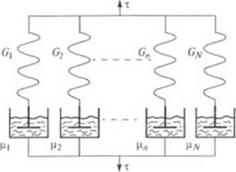
Рис. 1.15. Обобщенные модели вязкоупругих жидкостей:

и — Кельвина—Фойгта; б — Максвелла

ную цепь фойгтовских элементов (рис. 1.15, а, б). Такое соедине­ние используется потому, что параллельно соединенные макс­велловские элементы проявляют те же свойства, что и одиноч­ный элемент Максвелла, и последовательное соединение эле­ментов Фойгта ведет себя подобно простому фойгтовскому элементу.

Реологическое уравнение обобщенной модели Максвелла на­ходится из рассмотрения системы, состоящей из N параллельно соединенных максвелловских элементов (рис. 1.15, б).

Для /»-го элемента связь между напряжением и деформацией выражается в виде

где т„ — напряжение сдвига л-го элемента; ц„ — вязкость л-го элемента; 6’„ — мо­дуль сдвига л-го элемента.

Полное напряжение т(/) будет суммой отдельных составляю­щих:

Следовательно, если рассмотреть систему из N элементов, под­вергнутую в начальный момент времени (/ =0) деформации у0, ос­тающейся затем неизменной, то убывание напряжения во времени

представляющая собой реологическое уравнение обобщенной максвелловской жидкости. Для обобщенной максвелловской мо — | in вводится понятие функции релаксации у(/) вязкоупругого м. нериала, определяемой как отношение напряжения, выражен­ной) в виде функции от /, к начальной деформации при условии, •но материал подвергнут мгновенной деформации у0 в момент времени t = 0:

I огда для обобщенного максвелловского тела получаем:

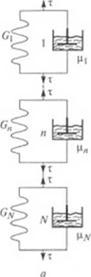
величину (7(ХР) можно определить из релаксационных изме — Р ими. Реологическое уравнение обобщенной модели Кельви­на Фойгта получается аналогичным образом. Для этого рас — мофим последовательную цепь из N фойгтовских элементов (рис. 1.15, а).

В модели Кельвина—Фойгта п-й элемент характеризуется мо — iv к’м сдвига G„ и вязкостью ц„. Тогда время запаздывания этого

• « мента л-. равно in/G„. Пусть напряжение ти, внезапно прило-

• иное в начальный момент (/ = 0), остается затем неизменным.

I hi п-го элемента из формулы (1.87) с учетом того, что уо = tJG„, получим:

Полное смещение системы у будет суммой деформаций отдель­ных элементов:

Обычно принято обозначать 1/(7,, = /„, где 1„ — податливость сдвигу.

уравнение (1.49) записывается в виде

Использование понятий функций распределения времени и распределения податливости /(Л,„) весьма упрощает описание реологического поведения материала. Такой метод нашел ус­пешное применение при изучении аморфных линейных поли­меров.

Для обобщения фойгтовской модели вводится понятие функции ползучести вязкоупругого материала, определяемой как отноше­ние деформации, выраженной в виде функции от /, к напряжению при условии, что к материалу после релаксации внезапно прило­жено постоянное по величине напряжение.

Если деформация у (0 получается после приложения напряже­ния т0 в начальный момент времени (t = 0), то функция ползучес­ти будет равна:

Гогда из уравнения (1.99) для обобщенной модели Фойгта по­лучим:

п распределение времени запаздывания /(л,„) можно определить на основе найденной экспериментальным путем ползучести ф(/).

Кроме рассмотренных выше существует еще множество сме­шанных моделей (тела Бюргсрса, Пойнтинга—Томпсона, Шведо­ва—Бингама и др.), предложенных различными исследователями а 1я описания повеления реальных тел.

Видео:Закон БернуллиСкачать

Теория и практика экструзии полимеров

СИСТЕМЫ ОХЛАЖДЕНИЯ РУКАВНЫХ ПЛЕНОК

Системы охлаждения экструзионных агрегатов для производ­ства рукавных пленок должны обеспечивать: — заданную интенсивность охлаждения с целыо получения ка­чественного изделия при заданной производительности экструдера; — заданную структуру пленки; — равномерность охлаждения …

РАСЧЕТ ПРОЦЕССА НАМОТКИ ПЛЕНКИ

При расчете процесса намотки пленки задают длину полотна или массу готового продукта. Если расчет рулона проводят по мас­се, то часто бывает необходимо исходя из диаметра рулона оце­нить толщину намотанной пленки. …

РАСЧЕТ ПРОЦЕССА ОХЛАЖДЕНИЯ РУКАВНЫХ ПЛЕНОК

При изготовлении рукавной пленки длина зоны охлаждения определяется системой и интенсивностью охлаждения. Обычно используют охлаждение рукава с помощью кольцевого сопла («воздушного кольца#). Преимущества этого метода охлаждения перед другими (распылением воды, …

Видео:Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

Продажа шагающий экскаватор 20/90

Цена договорная
Используются в горнодобывающей промышленности при добыче полезных ископаемых (уголь, сланцы, руды черных и
цветных металлов, золото, сырье для химической промышленности, огнеупоров и др.) открытым способом. Их назначение – вскрышные работы с укладкой породы в выработанное пространство или на борт карьера. Экскаваторы способны
перемещать горную массу на большие расстояния. При разработке пород повышенной прочности требуется частичное или
сплошное рыхление взрыванием.
Вместимость ковша, м3 20
Длина стрелы, м 90
Угол наклона стрелы, град 32
Концевая нагрузка (max.) тс 63
Продолжительность рабочего цикла (грунт первой категории), с 60
Высота выгрузки, м 38,5
Глубина копания, м 42,5
Радиус выгрузки, м 83
Просвет под задней частью платформы, м 1,61
Диаметр опорной базы, м 14,5
Удельное давление на грунт при работе и передвижении, МПа 0,105/0,24
Размеры башмака (длина и ширина), м 13 х 2,5
Рабочая масса, т 1690
Мощность механизма подъема, кВт 2х1120
Мощность механизма поворота, кВт 4х250
Мощность механизма тяги, кВт 2х1120
Мощность механизма хода, кВт 2х400
Мощность сетевого двигателя, кВ 2х1600
Напряжение питающей сети, кВ 6
Более детальную информацию можете получить по телефону (063)0416788

📺 Видео

Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

Измерение вязкостиСкачать

Вязкость газов и жидкостей, Киевнаучфильм, 1980Скачать

Распределение Максвелла — Больцмана (часть 6) | Термодинамика | ФизикаСкачать

Урок 137. Движение тела в жидкости и газе.Скачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Определение коэффициента вязкости жидкости методом СтоксаСкачать

Определение коэффициента вязкости жидкости с помощью капиллярного вискозиметраСкачать

Вязкость нефти и нефтепродуктовСкачать

68 учеников этого НЕ ЗНАЮТ! Таблица Менделеева — Как пользоваться?Скачать

Газовые законыСкачать

Подобие процессов конвективного теплообменаСкачать

Моделирование течения двухфазных сред. Расчет вязкости эмульсийСкачать

Методы исследования технологических процессов. Теория подобия. Виды подобияСкачать

Распределение энергии по степеням свободы. Диффузия и теплопроводность. Вязкость жидкости. Лекция 14Скачать