Уравнение закона вант гоффа применимо для (5 видео)

ВАНТ-ГОФФА ПРАВИЛО

ВАНТ-ГОФФА ПРАВИЛО. Почти все химические реакции при повышении температуры идут быстрее. Зависимость скорости реакции от температуры описывается уравнением Аррениуса:

k = Ae –E a/RT, где k – константа скорости реакции, А – не зависящая от температуры константа (ее называют предэкспоненциальным множителем), Е_а– энергия активации, R – газовая постоянная, Т – абсолютная температура. В школьных учебниках зависимость скорости реакции от температуры определяют в соответствии с так называемым «правилом Вант-Гоффа», которое в 19 в. сформулировал голландский химик Якоб Вант-Гофф. Это чисто эмпирическое правило, т.е. правило, основанное не на теории, а выведенное из опытных данных. В соответствии с этим правилом, повышение температуры на 10° приводит к увеличению скорости в 2–4 раза. Математически эту зависимость можно выразить уравнением v₂v₁ = g (T₂ – T ₁ )/10 , где v₁ и v₂– скорости реакции при температурах Т₁ и Т₂; величина g называется температурным коэффициентом реакции. Например, если g = 2, то при Т₂– Т₁ = 50 о v₂/v₁ = 2 5 = 32, т.е. реакция ускорилась в 32 раза, причем это ускорение никак не зависит от абсолютных величин Т₁ и Т₂, а только от их разности.

Однако из уравнения Аррениуса следует, что температурный коэффициент реакции зависит как от энергии активации, так и от абсолютной температуры. Для данной реакции с определенным значением Е_а ускорение при повышении температуры на 10° будет тем больше, чем ниже температура. Это почти очевидно и без расчетов: повышение температуры от 0 до 10° С должно сказаться на скорости реакции значительно сильнее, чем такое же повышение температуры, например, от 500 до 510° С.

С другой стороны, для данного температурного интервала ускорение реакции будет тем сильнее, чем больше ее энергия активации. Так, если энергия активации реакции мала, то такая реакция идет очень быстро, и при повышении температуры на 10° С ее скорость почти не изменяется. Для таких реакций температурный коэффициент намного меньше 2. Для реакций же с большой энергией активации, которые при невысоких температурах идут медленно, ускорение при повышении температуры на 10° С может значительно превысить 4-кратное.

Например, реакция диоксида углерода со щелочным раствором с образованием гидрокарбонат-иона (СО₂ + ОН® НСО₃ – ) имеет энергию активации 38,2 кДж/моль, поэтому при повышении температуры, например, от 50 до 60° С эта реакция ускорится всего в 1,5 раза. В то же время реакция распада этилбромида на этилен и бромоводород (С₂Н₅Вr ® С₂Н₄ + НВr) с энергией активации 218 кДж/моль ускорится при повышении температуры от 100 до 110 o С в 6,3 раза (правда, в этом интервале температур реакция идет очень медленно). Кинетика реакции атомов водорода с этаном H + C₂H₆ ® H₂ + C₂H₅ была изучены в широком температурном интервале – от 300 до 1100 К (27–827° С). Для этой реакции E_а = 40,6 кДж/моль. Следовательно, повышение температуры на 10° вызовет увеличение скорости реакции в 1,7 раза в интервале 300–310 K и только в 1,04 раза в интервале 1090–1100 K. Так что при высоких температурах скорость этой реакции практически не зависит от температуры. А для реакции присоединения атома водорода к двойной связи H + C₂H₄ ® C₂H₅ энергия активации мала (E_а = 3,4 кДж/моль, так что ее скорость слабо зависит от температуры в широком температурном интервале. И только при температурах намного ниже 0° С начинает сказываться наличие активационного барьера.

Подобных примеров можно привести множество. Очевидно, что правило Вант-Гоффа противоречит не только уравнению Аррениуса, но и многим экспериментальным данным. Откуда же оно взялось и почему нередко выполняется?

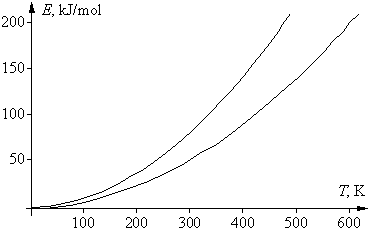
Если в приведенном выше математическом выражении для правила Вант-Гоффа подставить вместо скоростей v₁ и v₂ для данной реакции их зависимости от температуры, в соответствии с уравнением Аррениуса, то после сокращения предэкспоненциальных множителей получим следующее выражение: g = v_T +10/v_T = е –Е а/R(Т+10)/е –Е а/RТ = е (Еа/R)[1/Т – 1/(T+10)] . Логарифмироване этого уравнения дает: lng = (E_а/R)[1/T – 1/(T + 10)], откуда Еа = Rlng T(T + 10)/10 = 0,83lngT(T + 10). Энергия активации не является функцией температуры, эта зависимость нужна лишь для удобства последующего анализа. Последнее уравнение – это уравнение параболы, в котором физический смысл имеют только положительные значения. Соответствующая диаграмма ограничена двумя ветвями параболы: при g = 2 получаем Е_а = 0,58Т(Т + 10), при g = 4 получаем Е_а = 1,16Т(Т + 10). К тем же формулам приходим и при использовании десятичных логарифмов. Соответствующие графики двух парабол, для значений g 2 и 4, приведены на рисунке. Их физический смысл заключается в том, что области выполнения правила Вант-Гоффа соответствует только область между параболами. Таким образом, существуют только определенные соотношения между энергией активации реакции и температурой ее проведения, при которых правило Вант-Гоффа выполняется. Ниже нижней ветви температурный коэффициент g 4.

Если посмотреть, какие реакции «укладываются» в указанную довольно узкую область, то окажется, что все эти реакции идут не слишком быстро и не слишком медленно, а с удобной для измерения (при данной температуре) скоростью. Скорость только таких реакций и могли изучать химики во времена Вант-Гоффа. Например, если энергия активации была невелика (меньше 50 кДж/моль), то такая реакция при комнатной температуре заканчивалась за 1–2 секунды; поэтому для изучения ее кинетики следовало значительно понизить температуру, чтобы реакция проходила не быстрее, чем за 10–20 минут. Только в этом случае химики 19 в. успевали отбирать пробы по ходу реакции и анализировать изменение в них концентрации реагентов. Других способов изучения скорости реакции в то время не было. Если это не удавалось (например, водный раствор замерзал), то скорость такой реакции не изучали. Если же энергия активации реакции была велика и при комнатной температуре она шла слишком медленно (многие сутки, или даже недели), то температуру повышали, чтобы реакция шла с удобной для измерения скоростью. И здесь были свои ограничения – например, раствор мог закипеть, т.е. в любом случае исследователи фактически «подстраивали» изучаемую реакцию под область между двумя параболами.

Сейчас химики имеют возможность с помощью различных приборов экспериментально изучать и очень быстрые (идущие в микросекундной области), и очень медленные реакции, для которых температурный коэффициент может быть значительно меньше 2 или значительно больше 4. Поэтому правило Вант-Гоффа, которое, в отличие от уравнения Аррениуса, не имеет четкого физического смысла, представляет лишь чисто исторический интерес и в современной науке не используется. В подавляющем большинстве учебников и монографий по химической кинетике, а также в 5-томной Химической Энциклопедии это правило даже не упоминается. И, тем не менее, если изучаемая реакция идет с удобной для измерения скоростью, например, заканчивается за 30–40 мин, а энергия активации ее еще не измерена, то для предварительной грубой оценки зависимости скорости такой реакции от температуры можно использовать правило Вант-Гоффа. Поэтому это правило приводится во всех школьных учебниках химии.

Содержание

Осмотическое давление (Пример)
Объяснение эффекта осмоса
Открытие расчета давления
Что такое осмотическое давление
Закон Вант-Гоффа для разбавленных растворов
Пример расчета осмотического давления
Похожие страницы:
Leave a Comment
Осмос. Осмотическое давление. Закон Вант-Гоффа. Зависит ли осмотическое давление от природы растворённого вещества?
📸 Видео

Видео:Правило Вант-Гоффа для ЕНТ по химии 2023 | Химия ЕНТ УмскулСкачать

Осмотическое давление (Пример)

Изучение свойств разбавленных растворов показало, что между газообразным состоянием вещества и состоянием его в растворах существует большое сходство.

Как молекулы газа вследствие своего движения занимают наибольший объем, оказывая при этом давление на стенки сосуда, в котором газ заключен, так и молекулы растворенного вещества стремятся занять наибольший объем. Объем газа определяется размерами сосуда, а объем, в котором могут распределяться молекулы растворенного вещества, — объемом, занимаемым раствором.

Если поместить в цилиндр концентрированный раствор какого-нибудь вещества, например раствор сахара, а поверх него осторожно налить слой чистой воды, то постепенно молекулы сахара равномерно распределятся по всему объему жидкости. Это явление, как известно, называется диффузией; диффузия продолжается до тех пор, пока концентрация молекул сахара не станет одинаковой во всех слоях жидкости.

Рис. . Прибор для демонстрации осмотического давления раствора

Равномерное распределение молекул сахара и воды во всем объеме жидкости может происходить двумя путями: или молекулы сахара, оставляя нижний слой воды, переходят в верхний, пока их концентрация в обоих слоях не сравняется, или молекулы воды проникают из верхнего слоя в нижний, пока не перемешаются равномерно с молекулами сахара.

Окончательный результат, очевидно, в обоих случаях будет один и тот же. В действительности выравнивание концентрации идет обоими путями, т. е. происходит как движение молекул сахара в воду, так и движение молекул воды в раствор сахара.

Видео:Решение задач на тему: "Правило Вант-Гоффа". 1 часть. 10 класс.Скачать

Объяснение эффекта осмоса

Представим теперь, что вода и раствор сахара разделены пористой перегородкой, через которую могут свободно проходить молекулы воды, но не могут проникать молекулы сахара. Подобного рода «полупроницаемая» перегородка может быть получена, например, пропиткой глиняного пористого цилиндра раствором медного купороса с последующим погружением цилиндра в раствор железистосинеродистого калия. В результате такой обработки в порах цилиндра оседает железистосинеродистая медь и стенки цилиндра становятся полупроницаемыми.

Если в обработанный таким образом цилиндр налить раствор сахара и погрузить цилиндр в чистую воду, то выравнивание кон центраций (или, вернее, уменьшение концентрации раствора сахара) будет происходить только вследствие перемещения молекул воды. Последние в большем числе диффундируют в раствор, чем обратно; поэтому объем раствора будет постепенно увеличиваться, а концентрация сахара в нем уменьшаться.

Такая односторонняя диффузия через полупроницаемую перегородку называется осмосом. При достаточном количестве воды переход ее в раствор через полупроницаемую перегородку, строго говоря, должен продолжаться бесконечно, если этому не воспрепятствует какая-нибудь сила, действующая в противоположном направлении.

Возьмем сосуд с полупроницаемыми стенками, переходящий вверху в длинную узкую вертикальную трубку (рис.). Наполним его раствором сахара и погрузим в сосуд с чистым растворителем. Вследствие осмоса объем раствора будет постепенно увеличиваться и раствор начнет заполнять вертикальную трубку.

По мере поднятия уровня раствора в трубке будет создаваться избыточное гидростатическое давление, измеряемое разностью уровней раствора и растворителя и противодействующее проникновению молекул растворителя в раствор. Когда гидростатическое давление достигнет определенной величины, осмос прекратится. Сила, обусловливающая осмос, называется осмотическим давлением раствора. Величина осмотического давления определяется тем внешним давлением на раствор, при котором осмос прекращается .

Явления осмоса играют очень важную роль в жизни животных и особенно растительных организмов. Оболочки клеток представляют собой перепонки, легко проницаемые для воды, но почти непроницаемые для веществ, растворенных в клеточном соке. Проникая в клетки, вода создает в них довольно большое давление, которое слегка растягивает оболочки клеток и поддерживает их в напряженном состоянии.

Вот почему такие мягкие органы растения, как травянистые стебли, листья, лепестки цветов, обладают известной упругостью. Если срезать растение, то вследствие испарения воды через оболочки клеток объем клеточного сока уменьшается, оболочки клеток опадают, становятся дряблыми — растение вянет. Но стоит только начавшее вянуть растение поставить в воду, как начинается осмос, оболочки клеток снова напрягаются и растение принимает прежний вид.

Осмос является также одной из причин, обусловливающих поднятие воды по стеблю растения, рост клеток и многие другие явления.

Первые точные измерения величины осмотического давления, произведенные Пфейфером, привели к установлению двух следую щих положении:

1. Осмотическое давление раствора прямо пропорционально концентрации растворенного вещества.

2. Осмотическое давление пропорционально абсолютной температуре раствора.

Видео:Закон Вант-ГОФФАСкачать

Открытие расчета давления

В 1886 г. голландский физико-химик Вант-Гофф впервые обратил внимание на полную аналогию между этими положениями и газовыми законами Бойля-Мариотта и Гей-Люссака. Использовав числовые данные, полученные при измерениях осмотического давления, он показал, что величина осмотического давления для разбавленных растворов может быть выражена уравнением, совершенно сходным с уравнением состояния газа

где Р — осмотическое давление, а V — объем раствора, содержащего 1 грам-молекулу растворенного вещества. При этом оказывается, что постоянная R имеет то же самое числовое значение, что и в уравнении газового состояния

Отсюда следует, что закон Авогадро также применим к разбавленным растворам. И действительно, опыт показывает, что эквимолекулярные (т. е. содержащие одно и то же число молекул в 1 л) растворы различных веществ при одинаковой температуре обладают и одинаковым осмотическим давлением. В частности, растворы, содержащие 1 грам-молекулу растворенного вещества в 22,4 л, обладают при 0° осмотическим давлением, равным 1 ат.

Растворы, имеющие одинаковое осмотическое давление, называются изотоническими.

Видео:Уравнение Вант-ГоффаСкачать

Что такое осмотическое давление

Таким образом осмотическое давление, подобно давлению газа, при неизменном объеме и постоянной температуре зависит только от числа молекул растворенного вещества, но не зависит ни от природы растворенного вещества, ни от природы растворителя.

Если заменить в предыдущем уравнении молекулярный объем V концентрацией С, выраженной в молях на 1 л (V =1/С), то получим более удобное для вычисления осмотического давления выражение:

Видео:Вывод уравнения Вант-Гоффа для осмотического давленияСкачать

Закон Вант-Гоффа для разбавленных растворов

Глубокая аналогия между газами и растворами ясно выражена в следующем положении, носящем название закона Вант-Гоффа:

Осмотическое давление раствора равно тому давлению, которое производило бы растворенное вещество, если бы оно при той же температуре находилось в газообразном состоянии и занимало объем, равный объему раствора.

Этим законом и выражается сущность теории растворов Вант-Гоффа. Необходимо, однако, подчеркнуть, что, несмотря на полную аналогию числовых зависимостей, механизмы газового и осмотического давлений совершенно различны.

Яков Генрих Вант-Гофф (Jacobus Henricus Van’t Hoff) — один из основоположников современной физической химии, родился в г. Роттердаме (Голландия) 30 августа 1852 г. Окончив техническое училище в Дельфте, он изучал затем химию в университетах Бонна, Парижа и Утрехта. В 1874 г. получил степень доктора математики и натуральной философии в Утрехтском университете.

С 1896 г. и до конца своей жизни Вант-Гофф занимался солевыми равновесиями в растворах.

Вант-Гофф состоял членом-корреспондентом Петербургской Академии наук и с 1898 г. почетным членом Московского Общества испытателей природы.

Закон Вант-Гоффа справедлив только для разбавленных растворов. В концентрированных растворах наблюдаются значительные отклонения от него. Еще большие отклонения обнаруживаются в водных растворах электролитов — веществ, проводящих ток в водном растворе, о чем подробно будет сказано в следующей главе.

Яков Генрих Вант-Гофф (1852—1911)

Благодаря зависимости между молярной концентрацией раствора и его осмотическим давлением можно по величине осмотического давления вычислять молекулярные веса многих веществ, которые не превращаются в газообразное состояние, но легко растворяются в том или ином растворителе.

Наоборот, зная молярную концентрацию раствора, можно рассчитать его осмотическое давление. При расчетах полезно иметь в виду, что осмотическое давление раствора, содержащего в литре 1 моль растворенного вещества, может быть принято равным 22,4 ат (хотя фактически при такой концентрации раствора оно несколько больше).

Видео:Задачи на правило Вант-Гоффа. Зависимость скорости реакции от температуры.Скачать

Пример расчета осмотического давления

Рассчитать осмотическое давление раствора, содержащего в литре 9 г глюкозы.

Молекулярный вес глюкозы 180; следовательно, 9 г составляют 0,05 моля. Так как осмотическое давление пропорционально количеству растворенного вещества, то искомое осмотическое давление (х) находим из пропорции:

Непосредственное измерение осмотического давления представляет довольно большие трудности, но в этом и нет настоятельной необходимости. Как показал Вант-Гофф, осмотическое давление тесно связано с некоторыми другими свойствами разбавленных растворов, сравнительно легко поддающимися измерению, а именно: с понижением давления пара, понижением температуры замерзания, повышением температуры кипения.

Определив любую из этих величин, можно по ней рассчитать и осмотическое давление раствора. Так как все эти величины, подобно осмотическому давлению, изменяются пропорционально числу частиц растворенного вещества, то они также могут быть использованы для определения молекулярного веса растворенных веществ.

Вы читаете, статья на тему Осмотическое давление

Осмос. Осмотическое давление. Закон Вант-Гоффа. Зависит ли осмотическое давление от природы растворённого вещества?

Осмосом называют преимущественно одностороннее проникновение молекул растворителя(диффузию) через полунепроницаемую мембрану из растворителя в раствор или из раствора с меньшей концентрацией в раствор с большей концентрацией.

Осмотическим давлением называют величину, измеряемую минимальным гидравлическим давлением, которое нужно приложить к раствору, чтобы осмос прекратился.

Осмотическое давление разбавленных растворов неэлектролитов прямо пропорционально молярной концентрации, коэффиценту пропорциональности и абсолютной температуре: π =С(Х)RT,

Где π- осмотич давление,кПа; С(Х)- молярная концентрация, моль/л

С(Х)= n/V, где n-число молей неэлектролита, V- объём раствора; R- универсальная газовая постоянная,равная 8,31кПа*л/(моль*К); T-абсолютная температура, K.

π = n/V * RT или πV= nRT.

Чтобы согласовать количественное описание коллигативных свойств электролитов и законы идеальных растворов, Вант-Гофф ввёл поправочный коэффицент i, называемый изотоническим коэффицентом

Осмотическое давление зависит от концентрации растворенного вещества и температуры. Так, при увеличении концентрации с сахарозы в воде в два раза осмотическое давление возрастает примерно в два раза, при увеличении концентрации c в три раза осмотическое давление возрастает почти во столько же и т. д.

28. Гипо-, гипер- и изотонические растворы. Изотонический коэффицент

Изотонический раствор- жидкость внутренней среды или искусственно приготовленный раствор имеет такое же осмотическое давление, как нормальная плазма крови, подобную жидкую среду или раствор

Гипертонический раствор жидкость с более высоким осмотическим давлением

Гипотонический раствор жидкость с более низким осмотическим давлением

Изотонический коэффициент или коэффициент Вант-Гоффа (i)– это отношение суммы числа ионов и непродиссоциировавших молекул электролита к начальному числу молекул электролита, по его величине вычисляют степень электролитической диссоциации:

Формулы для расчета коллигативных свойств разбавленных растворов электрполитов с учетом изотонического коэффициента имеют вид:

— осмотическое давление Росм = ί С_м RT;

— 1-й закон Рауля ΔР / Р(z) = ί Сm ;

Нетрудно увидеть, что изотонический коэффициент ί может быть вычислен как отношение ΔР, Δt_кp, Δt_кип, Р_осм, найденных экспериментально на опыте, к тем же величинам, вычисленным без учета диссоциации электролита (Δр_выч, Δt_{кp выч}, Δt_{кип выч}; Р_{осм выч}):

29. Роль осмоса в биологических системах. Плазмолис и лизис. Осмотическое давление обеспечивает переход растворителя через полунепроницаемую мембрану от р-ра менее концентрированного к р-ру более концентрированному, поэтому оно играет важную роль в распределении воды между внутренней средой и клетками организма. Лизис-набухание клеток, разрыв оболочек, вытекание клеточного содержимого, вследствии помещения клеток в гипотонический р-р. Плазмолис-сморщивание клеток, при их помещении в гипертонический р-р.

30. Что называют буферными растворами? Буферные р-ры-это р-ры рН которых меняется незначительно при разбавлении или при добавлении небольших количеств китслоты или щелочи.

Гипертонический раствор жидкость с более высоким осмотическим давлением

Гипотонический раствор жидкость с более низким осмотическим давлением

— осмотическое давление Росм = ί С_м RT;

— 1-й закон Рауля ΔР / Р(z) = ί Сm ;

36. Объясните, почему большинство буферных систем организма имеет буферную емкость по кислоте больше, чем по основанию.
Потому что в живом организме в результате метаболизма образуются большие количества кислых продуктов. Так, в организме человека за сутки образуется такое количество различных кислот, которое эквивалентно 20-30 л однонормальной сильной кислоты. И для того чтобы поддерживать рH организма, у буферных систем организма буферная емкость по кислоте больше, чем по основанию.
37. Патологические явления: ацидоз и алкалоз
Алкалоз — одна из форм нарушения кислотно- щелочного равновесия организма; характеризуется абсолютным или относительным избытком оснований, т.е. Веществ, присоединяющих ионы водорода(протоны), по отношению к кислотам, отщепляющим их. Алкалоз может быть компенсированным или некомпенсированным в зависимости от значения pH. При компенсированном алкалозе pH крови удерживается в пределах нормальных величин (7,35-7,45), отмечаются лишь сдвиги в буферных системах и физиологических регуляторных механизмах. При некомпенсированном алкалозе pH превышает 7,45, что обычно связано со значительным избытком оснований инедостаточностью физико-химических и физиологических механизмов регуляции кислотно- щелочного равновесия. Ацидоз — сдвиг кислотно-щелочного равновесия в организме в сторону относительного увеличения количества анионов кислот, характеризуется абсолютным или относительным избытком кислот, т.е. веществ, отдающих ионы водорода (протоны), по отношению к основаниям, присоединяющим их. Ацидоз также может быть компенсированным или некомпенсированным в зависимости от значения pH. При компенсированном ацидозе pH крови смещается к нижней границе физиологической нормы (7,35). При более выраженном сдвиге в кислую сторону (pH менее 7,35) ацидоз считается некомпенсированным. Такой сдвиг обусловлен значительным избытком кислот и недостаточностью физико-химических и физиологических механизмов регуляции кислотно- щелочного равновесия.

38. Какое химическое равновесие поддерживают в организме буферные системы?
В организме буферные системы поддерживают кислотно-щелочное равновесие. В организме человека особенно большую роль играют белковый, гидрокарбонатный, гемоглобиновый и фосфатный буферы.

39. Какая буферная система вносит максимальный относительный вклад в поддержание протолитического гомеостаза во внутренней среде эритроцитов? Максимальный относительный вклад в поддержание протолитического гомеостаза во внутренней среде эритроцитов вносит гемоглобиновая буферная система.

40.Какие соединения называются координационными? Приведите примеры.
Комплексные соединения или координационные соединения — частицы (нейтральные молекулы или ионы), которые образуются в результате присоединения к данному иону (или атому), называемому комплексообразователем, нейтральных молекул или других ионов, называемых лигандами. Примеры: [Cu(NH3)4] SO4 — сульфат тетраамминмеди (II) K4[Fe(CN)6] — Гексацианоферра́т(II) ка́лия [Pt(NH3)2Cl2] — транс-Дихлородиамминплатина(II)

41. Классификация координационных соединений
Координационные соединения классифицируют: Катионные комплексы образованы вñ1)По заряду комплекса: результате координации вокруг положительного иона нейтральных молекул (H2O, NH3и др.). [Zn(NH3)4]Cl2 — хлорид тетраамминцинка(II) [Co(NH3)6]Cl2 — хлорид гексаамминкобальта(II) Анионные комплексы: в ролиñ комплексообразователя выступает атом с положительной степенью окисления, а лигандами являются простые или сложные анионы. K2[BeF4] — тетрафторобериллат(II) калия Li[AlH4] — тетрагидридоалюминат(III) лития K3[Fe(CN)6] — гексацианоферрат (III) калия Нейтральные комплексы образуются приñ координации молекул вокруг нейтрального атома, а также при одновременной координации вокруг положительного иона — комплексообразователя отрицательных ионов и молекул. [Ni(CO)4] — тетракарбонилникель [Pt(NH3)2Cl2] — дихлородиамминплатина(II) 2) По числу мест, занимаемых лигандами в координационной сфере Монодентатные лиганды.ñ Полидентатные лиганды.ñБидентатные лиганды.ñ

42. Природа химической связи в комплексных соединениях
Во внутренней сфере комплексного соединения связь между комплексообразователем и лигандами ковалентная, образованная по донорно-акцепторному механизму. Ион или атом- комплексообразователь является акцептором, а лиганды являются донорами электронных пар.

№43) Как расчитывается общая и стуаенчатая константа нестойкости(устойчивости).

Ступенчатые константы нестойкости этих комплексов равняются соответственно &. Высокие значения & Г1 и k2 — l свидетельствуют о том, что при образовании комплексов с медью ( II) этилендиамин выступает как полидентатный лиганд. Произведение ступенчатых констант нестойкости равно общей константе нестойкости, индекс которой показывает, из каких множителей она образовалась.Зная величины ступенчатых констант нестойкости ( в частности константы, отвечающей отщеплению первой молекулы аммиака или амина от комплексного иона), концентрацию комплекса, константу RH как основания и константу Me. Зная функцию закомплексованности, ступенчатые константы нестойкости вычисляются методом Ледена. Так, при рассмотрении ступенчатых констант нестойкости комплексных аммиакатов Ni ( II), Cu ( II) пли Со ( П) видно, что для этих солей сольватацпонное равновесие с отщеплением свободного основания будет выражено гораздо сильнее, чем усиление степени кислотной диссоциации аммиака пли аминов в поле двухвалентных ионов. Так, при рассмотрении ступенчатых констант нестойкости комплексных аммиакатов Ni ( II) Cu ( II) или Со ( П) видно, что для этих солей сольватационное равновесие с отщеплением свободного основания будет выражено гораздо сильнее, чем усиление степени кислотной диссоциации аммиака или аминов в поле двухвалентных ионов.]

Эл 1, Рп-называют ступенчатыми константами нестойкости.

Рп ] ( Рп называют ступенчатыми константами нестойкости.

Значение общей константы нестойкости равно произведению значений всех ступенчатых констант нестойкости. [9]

Последние применительно к диссоциации комплексных ионов называются их ступенчатыми константами нестойкости

А — ион водорода или адденд, Ki — кажущаяся ступенчатая константа нестойкости комплексного соединения МА, которая может считаться в первом приближении величиной постоянной только при постоянной ионной силе раствора. Термодинамические уравнения, описывающие соответствующие процессы, идентичны для обоих процессов. [11По кривой комплексообразования, как было показано Бьеррумом, можно определить ступенчатые константы нестойкости аммиакатов меди с различным числом молекул МНз в координационной сфере и, зная их, рассчитать концентрации комплексов различного состава при любых концентрациях свободного аммиака в растворе. [12]Каждой стадии диссоциации комплекса соответствует ступенчатая константа диссоциации, которую называют ступенчатой константой нестойкости и обозначают йнест. Чем сильнее диссоциирует комплекс, тем большее значение имеет / г ест — Константы нестойкости используют для характеристики устойчивости любой комплексной частицы в растворе независимо от того, какие лиганды она отщепляет. [13]Каждой стадии диссоциации комплекса соответствует ступенчатая константа диссоциации, которую называют ступенчатой константой нестойкости и обозначают йвест. Чем сильнее диссоциирует комплекс, тем большее значение имеет Анест. Константы нестойкости используют для характеристики устойчивости любой комплексной частицы в растворе независимо от того, какие лиганды она отщепляет. [14]

Дата добавления: 2015-12-26 ; просмотров: 4520 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ