| Название | Лабораторная работа 2 изучение закона сохранения энергии с помощью маятника максвелла |
| Анкор | ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА |
| Дата | 01.01.2022 |
| Размер | 33.57 Kb. |
| Формат файла |  |
| Имя файла | Выполненная работа №2.docx |
| Тип | Лабораторная работа #322721 |
| Подборка по базе: Аудиторная работа.doc, контрольная работа.docx, Теория государства и права. ПИСЬМЕННАЯ РАБОТА №1 (Эссе)1 (2).do, контрольная работа по уголовному праву.docx, Практическая работа физ воспит.docx, дип. работа Адема.pptx, сама работа. docx, Практическая работа.docx, Практическая работа теория управления Матвеева О.А..docx, Расчет эн-я хоз. контрольная работа.docx Лабораторная работа № 2 ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ С ПОМОЩЬЮ Цель работы: Ознакомление со сложным движением твердого тела и изучение закона сохранения энергии на примере движения маятника Максвелла. Описание установки и метода изучения процесса вниз и вращательное вокруг своей оси симметрии. Уравнения движения маятника без учета сил трения имеют вид: где m – масса маятника; I – момент инерции маятника; g – ускорение силы тяжести; r – радиус стержня; T – сила натяжения нити (одной); a – ускорение поступательного движения центра масс маятника; ε – угловое ускорение маятника. Ускорение a может быть получено по измеренному времени движения t и проходимому маятником расстоянию h из уравнения: a = выражение для расчета теоретического значения ускорения движения центра тяжести маятника: a = Скорость: V = a t ; угловая скорость: ω = ε t . Полная кинетическая энергия маятника складывается из энергии поступательного перемещения центра масс (совпадающего с центром оси) и из энергии вращения маятника вокруг оси: J = Выполнение работы
Экспериментальное значение ускорения m = Теоретическое значение ускорения: a = Расчёт относительной погрешности расхождения теоретического и экспериментального значений ускорения: Вывод: В лабораторной работе измерено время движения маятника Максвелла, нагруженного дополнительным диском и кольцом. Рассчитаны экспериментальное и теоретическое значения ускорения маятника, они отличаются незначительно. Произведён расчёт линейной и угловой скорости, углового ускорения, момента инерции и кинетической энергии.
Момент инерции — скалярная физическая величина , мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.
Маятник Максвелла представляет собой металлический диск 1, в середине которого укреплен металлический стержень 2. К концам этого стержня прикреплены две крепкие (капроновые) нити 3. Они наматываются на стержень (от концов его к диску). Диск маятника представляет собой непосредственно сам диск и сменные кольца, которые закрепляются на диске. При освобождении маятника он начинает движение: поступательное вниз и вращательное вокруг своей оси симметрии.
Из уравнений движения: T = ε = Содержание Видео:Маятник МаксвеллаСкачать  Основные теоретические сведенияЛист учета выполнения лабораторной работы ИЗУЧЕНИЕ СОХРАНЕНИЯ ЭНЕРГИИ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА
Общее количество лабораторных __________ (одинаковое для всех студентов группы) Выполнил студент___________________ Лектор _____________________ группы __ИБС-12______ Ассистент __________________ 2 семестр 2012 — 2013 уч.года Лабораторная работа 4 ИЗУЧЕНИЕ СОХРАНЕНИЯ ЭНЕРГИИ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА Цель работы: изучение сложного движения твердого тела и закона сохранения энергии в таком движении, определение момента инерции маятника Максвелла. Основные теоретические сведения Рассмотрим плоское движение твердого тела, при котором все точки твердого тела перемещаются в параллельных плоскостях. Примером такого движения может служить качение цилиндра по плоскости. Плоское движение может быть представлено как суперпозиция двух движений – поступательного и вращательного. Движение центра масс твердого тела определяется уравнением: где Чтобы полностью определить движение тела, надо, кроме того, написать уравнение моментов относительно какой-либо произвольно выбранной неподвижной оси. Однако положение движущегося тела относительно неподвижной оси будет все время изменяться и связь между моментом импульса и угловой скоростью будет сложной. Для случая плоского движения задача существенно упрощается, так как можно записать уравнение моментов относительно оси, жестко связанной с телом и проходящей через его центр масс. Поскольку эта ось неподвижна относительно тела, можно записать основное уравнение динамики вращательного движения: где Таким образом, уравнение (4.1) определяет скорость поступательного движения тела, а уравнение (4.2) – угловую скорость вращательного движения. Применим полученные уравнения к движению маятника Максвелла. Маятник Максвелла представляет собой металлический диск 1, в середине которого укреплен стержень 2, а к ободу крепится съемное кольцо 3. К концам стержня прикреплены две капроновые нити 4. Они наматываются на стержень от концов его к диску. При освобождении маятника он начинает движение: поступательное вниз и вращательное вокруг своей оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения, когда нити уже размотаны, приводит вновь к наматыванию нитей на стержень, а следовательно, и к подъему маятника. Уравнения движения маятника без учета сил трения имеют вид: где т – масса маятника, I – момент инерции маятника, g –ускорение силы тяжести, r – радиус стержня, T – натяжение нити, а –ускорение поступательного движения центра масс маятника, e – угловое ускорение маятника. Ускорение а может быть получено по измеренному времени движения t и проходимому маятником расстоянию h из уравнения Уравнения (4.3), (4.4), (4.5) дают: Пользуясь этими уравнениями с учетом (4.6), можно определить момент инерции маятника Максвелла по экспериментально полученным данным: Расстояние h, проходимое маятником, измеряется по вертикальной рейке с делениями. Момент инерции маятника можно рассчитать теоретически. Момент инерции маятника I является аддитивной величиной: где Момент инерции оси маятника Момент инерции диска где Момент инерции где Полная кинетическая энергия маятника складывается из энергии поступательного перемещения центра масс, совпадающего с центром оси, и из вращения маятника вокруг оси: Зная линейное и угловое ускорения, можно найти скорость движения оси маятника и угловую скорость его вращения: Видео:Маятник Максвелла.Скачать  Научная работа по теме «Закон сохранения энергии. Маятник Максвелла»Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БАШКОРТОСТАН Муниципальное автономное общеобразовательное учреждение Татарская гимназия №84 Октябрьского района городского округа город Уфа Республики Башкортостан XIX научно-практическая конференция «Взгляд в будущее» Номинация «Наука и техника» Нуриманов Эмиль, Сошникова Кристина обучающиеся 11 класса Закон сохранения энергии. Маятник Максвелла Багаутдинова З.Г учитель физики МАОУ «Татарская гимназия №84» Видео:Урок 122. Закон сохранения полной механической энергииСкачать  ОглавлениеВидео:Вывод закона сохранения механической энергии | Физика 9 класс #22 | ИнфоурокСкачать  ВведениеВ мире мы окружены настолько интересными вещами, что они стали для нас привычными и мы не замечаем их уникальность. Мы не интересуемся происхождением электрочайника, пульта для телевизора, пылесоса, в конце концов мы используем эти вещи каждый день и нам не важно, на чём основана их работа. Иногда для изучения чего-то нового необходимо уделить достаточно большое количество времени. Так например, всем известная игрушка под названием Йо-йо, с помощью которой многие выполняют разные эффектные трюки. Первое определение Йо-йо — игрушка из двух одинаковых по размеру и весу дисков, скрепленных осью с привязанной к ней верёвкой. Это определение самого древнего варианта игрушки, который можно встретить и по сей день. Нам стало интересно, на чём основана её работа. Оказалось, что Йо-йо этого типа работает по принципу маятника Максвелла, оно раскручивается по верёвке и возвращается обратно и так, пока не остановится. Что же касается самого маятника Максвелла, так он представляет собой круглое твердое тело, насаженное на ось, которая в свою очередь подвешена на двух накручивающихся на нее нитях. Действие прибора основано на одном из основных законов механики на законе сохранения механической энергии: полная механическая энергия системы, на которую действуют только консервативные силы, постоянна. Под действием силы тяжести маятник совершает колебания в вертикальном направлении и вместе с тем вращательные колебания вокруг своей оси. Пренебрегая силами трения, систему можно считать консервативной. Закрутив нити, мы поднимаем маятник на высоту h, сообщив ему запас потенциальной энергии. При освобождении маятника он начинает движение под действием силы тяжести: поступательное вниз и вращательное вокруг своей оси. При этом потенциальная энергия переходит в кинетическую. Опустившись в крайнее нижнее положение, маятник будет по инерции вращаться в том же направлении, нити наматываются на ось и маятник поднимется. Так происходят колебания маятника. Зная, что такое маятник Максвелла и на чём основана его работа, мы решили изготовить различные маятники, изменяли толщину и длину нити и стержня, толщину дисков и их радиус, чтобы выяснить от чего зависит их работа и результаты нашего исследования привели в работе. Цель работы — изучить принцип работы маятника Максвелла на основе изучения закона сохранения энергии. 1. Обзор и анализ статей по изучению закона сохранения энергии и маятника Максвелла; 2. Проектирование и сборка простейшего маятника. 3. Проведение эксперимента и его презентация. 1. Метод сбора и анализа выбранных статей; 2. Метод конструирования прибора; 3. Метод наблюдения и анализа. О, великий Максвелл! Однако маятник Максвелла не был им изобретен, а был только назван в его честь. Это устройство используют для обучения школьников и студентов, им украшают оффисы, его дарят любознательным деткам. Идут годы, но только множатся всевозможные варианты этой научной игрушки! Маятник Максвелла (иначе колесо Максвелла) известен как классическая иллюстрация превращения механической энергии. Маятник состоит из диска, который закреплен на горизонтально оси, а ось подвешена с двух сторон на длинных нитях к опоре. Концы нитей закреплены на оси вращения. При накручивании нити на ось вращения и ее раскручивании маятник совершает колебательные движения вверх-вниз. Для запуска маятника необходимо накрутить нити на ось, подняв таким образом маятник в наивысшую точку (потенциальная энергия здесь максимальна), а затем отпустить. Под действием силы тяжести маятник начнет опускаться вниз, все быстрее вращаясь, с постоянным ускорением. Ускорение диска при его движении вниз не зависит от его массы и момента инерции, а зависит от соотношения радиуса оси вращения (r) и радиуса самого диска (R). По мере движения вниз потенциальная энергия ранее поднятого маятника переходит в кинетическую энергию поступательного и вращательного движения. Опускания и подъемы диска со все уменьшающейся амплитудой повторяются много раз, пока маятник, наконец, не останавливается, т.к. весь первоначальный запас энергии в результате трения превращается в тепловую энергию. Спустившись до самого низа — на сколько хватит длины нити (внизу кинетическая энергия маятника и его скорость максимальны), он продолжит вращение по причине инерции. При этом нити начнут накручиваться на ось вращения, и маятник станет подниматься вверх. Однако теперь он не достигнет первоначальной высоты, т.к. часть механической энергии маятник теряет за счет трения. Сделав несколько десятков колебательных движений (в зависимости от конструкции), маятник остановится. В нижней точке траектории маятник за очень короткий промежуток времени меняет свое направление движения. Здесь нить маятника испытывает сильный рывок. Сила натяжения нити в этот момент возрастает в несколько раз. Эта дополнительная сила натяжения нити тем меньше, чем меньше радиус оси вращения, и тем больше, чем большее расстояние проходит маятник от начала движения до самой низшей точки. Если нить тонкая, то она может даже порваться. Вместо обычного диска в маятнике Максвелла для вращения можно использовать и другие тела. Так существует, например, физическая игрушка (есть и аналогичные ей), повторяющая принцип действия маятника Максвелла. Это разноцветный попугайчик, закрепленный, на оси вращения. Правда такая красивая игрушка приобретает и проблему. Фигурка не симметрична, поэтому конструктору требуется поразмыслить, как совместить центр тяжести попугайчика с центром вращения. Уже многие годы существует и еще одна разновидность маятника Максвелла — Сизифов — маятник с намагниченной осью вращения. Как должен работать этот маятник? Имя Сизифа говорит само за себя. Точно по середине тонкой намагничивающейся хромированной оси насажен сильный магнит не очень большого диаметра. На магнит одевается пластиковая шайба-диск. Две хромированные железные штанги-направляющие (длиной около 50 см) закреплены на основании в вертикальном положении таким образом, что расстояние между ними внизу чуть больше длины оси с диском. К верху устройства расстояние между штангами слегка сужается. Проследим, как работает этот маятник. Сначала надо симметрично приставить ось с диском к штангам вверху с одной или с другой стороны и отпустить ее. Притягиваясь к железу, намагниченная ось с диском под действием силы тяжести начинает сначала медленно, а затем все быстрее скатываться, вращаясь, по штангам вниз. В зависимости от того, с какой стороны приставлена ось с диском к штангам, вращение диска будет вправо или влево. Возникшее в результате намагничивания притяжение оси к штангам обеспечивает не просто падение вниз, а вращение диска. Когда при скатывании диска вниз, расстояние между штангами становится чуть больше длины оси, то ось с диском проскакивает между штангами и попадает на их другую сторону. Сохранив направление вращения, диск, имеющий внизу максимальную скорость, проскальзывает между штангами на другую сторону и начинает подниматься вдоль них вверх. Это изменение направления движения диска полностью соответствует принципу движения классического маятника Максвелла. Разница состоит лишь в том, что трение намагниченной оси о штанги в этом случае зависит от силы намагничивания. Она должна быть при выборе конструкции маятника строго рассчитана, чтобы ось с диском не сорвалась в самой нижней точке своего движения. Всем, как говорится, хороши и маятник Максвелла, и Сизифов-маятник, одно плохо, покачавшись некоторое время, они все-таки останавливаются. И тут интересен еще один вариант маятника, который волшебным способом будет крутиться, как покажется стороннему наблюдателю, сколько душе угодно! Он так и называется «волшебный маятник» (Magic rail twirler). Незаметные движения рук, и маятник никогда не остановится! Конечно, это шутка… «Волшебный маятник» – это еще один вариант игрушки маятника Максвелла. В этом маятнике «легким нажатием руки» штанги можно раздвинуть, и диск поменяет направление своего движения. На хромированных направляющих штангах располагается диск с магнитной осью, концы которой часто выполнены в виде конусов. При работе игрушки очень хорошо видно, как меняется направление движения диска при увеличении расстояния между направляющими. Незаметным движением руки можно компенсировать потери энергии и достичь более многократного колебания диска вверх-вниз или из стороны в сторону. Более современные модели игрушек оснащены даже подсветкой изнутри диска. Вот так имя великого физика соединило детскую научную игрушку и серьезный физический прибор. Если захотите поэкспериментировать с маятником Максвелла, то сделать его в наше время не очень и трудно. Берете лазерный диск, скручиваете из листа школьной тетради трубочку и вставляете в центр диска. Трубочка слегка разворачивается и заполняет бумагой все отверстие. Отрезаете две одинаковые нити покрепче и капаете клеем, приклеивая нити к концам трубочки и центр диска к середине трубочки. Осталось подвесить…. А для детских умов знаменитый Я.И. Перельман загадал когда-то физическую загадку: «Нити маятника Максвелла прикреплены к пружинному безмену. Что должно происходить с указателем безмена в то время, когда диск-маховик исполняет свой танец вверх и вниз? Останется ли указатель в покое? Если будет двигаться, то в какую сторону?» Если вам не удалось сразу отгадать, то ответ Перельмана таков: «Когда диск опускается ускоренно вниз, чашка, к которой прикреплены нити, должна подниматься, так как освобождаемые нити не увлекают ее вниз с прежней силою. Когда же диск-маховик поднимается замедленно вверх, то он натягивает наматывающиеся на его ось нитки, и они увлекают чашку вниз. Короче говоря, чашка и привязанный к ней диск-маховик движутся навстречу друг к другу». А вы как думали? Видео:Физика. 7класс. Превращение одного вида механической энергии в другой (с помощью маятника Максвелла)Скачать  Закон сохранения энергииФилософские предпосылки к открытию закона были заложены ещё античными философами. Ясную, хотя ещё не количественную, формулировку дал в «Началах философии» (1644г) Рене Декарт. Аналогичную точку зрения выразил в XVIII веке М. В. Ломоносов. В письме к Эйлеру он формулирует свой «всеобщий естественный закон» (5 июля 1748 года), повторяя его в диссертации «Рассуждение о твердости и жидкости тел» (1760). Одним из первых экспериментов, подтверждавших закон сохранения энергии, был эксперимент Жозефа Луи Гей-Люссака, проведённый в 1807 году. Пытаясь доказать, что теплоёмкость газа зависит от объёма, он изучал расширение газа в пустоту и обнаружил, что при этом его температура не изменяется. Однако, объяснить этот факт ему не удалось. В начале XIX века рядом экспериментов было показано, что электрический ток может оказывать химическое, тепловое, магнитное и электродинамическое действия. Такое многообразие подвигло М. Фарадея выразить мнение, заключающееся в том, что различные формы, в которых проявляются силы материи, имеют общее происхождение, то есть могут превращаться друг в друга. Эта точка зрения, по своей сути, предвосхищает закон сохранения энергии. Первые работы по установлению количественной связи между совершённой работой и выделившейся теплотой были проведены Сади Карно. В 1824 году им была опубликована небольшая брошюра «Размышления о движущей силе огня и о машинах, способных развивать эту силу». Количественное доказательство закона было дано Джеймсом Джоулем в ряде классических опытов. Результаты которых были изложены на физико-математической секции Британской ассоциации в его работе 1843 года «О тепловом эффекте магнитоэлектричества и механическом значении тепла». Первым осознал и сформулировал всеобщность закона сохранения энергии немецкий врач Роберт Майер. Формулировку в точных терминах закону сохранения энергии первым дал Герман Гельмгольц. Закон сохранения энергии—основной закон природы, заключающийся в том, что энергия замкнутой системы сохраняется во времени. Другими словами, энергия не может возникнуть из ничего и не может в никуда исчезнуть, она может только переходить из одной формы в другую. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то правильнее называть его не законом, а принципом сохранения энергии. Частный случай — закон сохранения механической энергии — механическая энергия консервативной механической системы сохраняется во времени. Проще говоря, при отсутствии диссипативных сил(например, сил трения) механическая энергия не возникает из ничего и не может никуда исчезнуть. Существует множество мифов о вечных двигателях, но, несмотря на многочисленные попытки, никому не удавалось построить вечный двигатель, производящий полезную работу без воздействия извне. Вот некоторые модели вечных двигателей: Ученые стали догадываться, что вечный двигатель построить нельзя. В19 веке была построена наука термодинамика. Одной из основ термодинамики стал закон сохранения энергии, который являлся обобщением многих экспериментальных фактов. Термодинамику можно использовать для описания работы ряда механизмов, например, двигателей внутреннего сгорания или холодильных установок. Если известно, как и при каких условиях работает механизм, можно рассчитать, сколько работы он произведет. В1918 году Эмма Нётер доказала важную теорему для теоретической физики, согласно которой в системе, обладающей симметриями, появляются сохраняющиеся величины. Сохранению энергии соответствует однородность времени. Как нужно понимать «однородность времени»? Пусть у нас есть какое-нибудь устройство. Если я его включаю сегодня, завтра или через много лет, и оно работает каждый раз одинаково, то для такой системы время однородно, и в ней будет работать закон сохранения энергии. К сожалению, школьных знаний недостаточно, чтобы доказать теорему Нётер. Но доказательство математически строгое, и связь между однородностью течения времени и сохранением энергии однозначна. Попытка построить вечный двигатель, работающий сколь угодно долго, — это попытка обмануть природу. Такая же бессмысленная, как и попытка преодолеть 1000 километров за 10 минут на автомобиле со скоростью100 км/ч(помните формулу s = vt ?). Что же получается, энергия всегда сохраняется? Не установили ли физики границу познания со своим законом сохранения энергии? Конечно нет! В общем случае, если в системе нет однородности времени, энергия не сохраняется. Примером такой системы является Вселенная. Известно, что Вселенная расширяется. Сегодня она не такая, как в прошлом, и в будущем изменится. Таким образом, во Вселенной нет однородности времени, и для нее закон сохранения энергии неприменим. Более того, энергия всей Вселенной не сохраняется. Дают ли такие примеры отсутствия сохранения энергии надежду на построение вечного двигателя? К сожалению, не дают. Наземных масштабах расширение Вселенной совершенно незаметно, и для Земли закон сохранения энергии выполняется с огромной точностью. Вот так физика объясняет невозможность построения вечных двигателей. В 40-х годах XIX в. трудами Р. Майера, Г. Гельмгольца и Дж. Джоуля (в разное время и независимо друг от друга) был доказан закон сохранения и превращения энергии. Джоуль Джеймс Прескотт (1818–1889) – английский физик, один из первооткрывателей закона сохранения энергии. Первые уроки по физике ему давал Дж. Дальтон, под влиянием которого Джоуль начал свои эксперименты. Работы посвящены электромагнетизму, кинетической теории газов. Рассмотрим систему, состоящую из N -частиц. Силы взаимодействия между частицами – консервативные. Кроме внутренних сил, на частицы действуют внешние консервативные и неконсервативные силы, т.е. рассматриваемая система частиц или тел консервативна. Тогда для этой системы можно найти полную энергию системы: E = K + U внутр.+ U внешн.= const . Для механической энергии закон сохранения звучит так: полная механическая энергия консервативной системы материальных точек остаётся постоянной . Для замкнутой системы, т.е. для системы, на которую не действуют внешние силы, можно записать: E = K + U внутр.= const . , т.е. полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остаётся постоянной . Если в замкнутой системе действуют неконсервативные силы, то полная механическая энергия системы не сохраняется – частично она переходит в другие виды энергии, неконсервативные. Система, в которой механическая энергия переходит в другие виды энергии, называется диссипативной , сам процесс перехода называется диссипацией энергии . В диссипативной, изолированной от внешнего воздействия системе остаётся постоянной сумма всех видов энергии (механической, тепловой и т.д.) Здесь действует общий закон сохранения энергии. Этот процесс хорошо демонстрирует маятник Максвелла. Роль консервативной внешней силы здесь играет гравитационное поле. Маятник прекращает свое движение из-за наличия внутренних неконсервативных сил (сил трения, сопротивления воздуха). Видео:Физика 7 класс. Переход механической энергии во внутреннюю (с помощью маятника Максвелла)Скачать  Маятник Максвелла или колесо МаксвеллаЧто же касается самого маятника Максвелла, так он представляет собой круглое твердое тело, насаженное на ось, которая в свою очередь подвешена на двух накручивающихся на нее нитях. Действие прибора основано на одном из основных законов механики на законе сохранения механической энергии: полная механическая энергия системы, на которую действуют только консервативные силы, постоянна. Под действием силы тяжести маятник совершает колебания в вертикальном направлении и вместе с тем вращательные колебания вокруг своей оси. Пренебрегая силами трения, систему можно считать консервативной. Закрутив нити, мы поднимаем маятник на высоту h, сообщив ему запас потенциальной энергии. При освобождении маятника он начинает движение под действием силы тяжести: поступательное вниз и вращательное вокруг своей оси. При этом потенциальная энергия переходит в кинетическую. Опустившись в крайнее нижнее положение, маятник будет по инерции вращаться в том же направлении, нити наматываются на ось и маятник поднимется. Так происходят колебания маятника. Видео:Применение закона сохранения и превращения механической энергии. Практическая часть. 9 класс.Скачать  Теоретическое введениеПринцип работы основан на основном законе физики – законе сохранения энергии, который говорит, что механическая энергия замкнутой консервативной системы во время движения системы не изменяется. (Замкнутая – значит, нет внешних сил, совершающих работу и увеличивающих или уменьшающих механическую энергию системы; консервативная – нет диссипативных (трения, сопротивления и т.д.) сил, превращающих механическую энергию системы во внутреннюю (тепло). Маятник Максвелла представляет собой массивный диск, ось которого подвешена на двух накрученных на нее нитях. Если маятник опустить, то под его тяжестью нить будет раскручиваться, и он начнет совершать возвратно-поступательные движения в вертикальной плоскости при одновременном вращении диска вокруг оси. Движение всякой точки диска можно представить как поступательное движение со скоростью V , равной скорости центра масс, и вращение вокруг геометрической оси с угловой скоростью . Полную скорость любой точки получим, прибавив (векторно) к скорости V ` = r , обусловленной вращением, скорость поступательного движения V . В точке, где нить отделяется от оси, эта полная скорость равна нулю. Через эту точку проходит мгновенная ось вращения. Подсчитаем кинетическую энергию тела, совершающего плоское движение. Если рассматривать движение тела как чистое вращение вокруг мгновенной оси, то элемент массы m i имеет в данный момент линейную скорость V i = r i , где r i – расстояние от этого элемента до мгновенной оси. Кинетическая энергия отдельного элемента тела будет: а кинетическая энергия всего тела где – момент инерции тела относительно мгновенной оси. Но по теореме Штейнера I 1 = I o + mr o 2 , где r o – расстояние от мгновенной оси до центра тяжести (в нашем случае – это радиус оси, на которую намотаны нити) и I o – момент инерции тела относительно оси, проходящей через центр тяжести. Поэтому из (1) получим: Введя в это выражение линейную скорость центра тяжести V = r , получим Полная кинетическая энергия плоского движения твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения вокруг оси, проходящей через центр тяжести. По закону сохранения энергии в механике полная энергия Е изолированной системы, в которой действуют только упругие силы и силы всемирного тяготения, есть величина постоянная: Видео:Лабораторная работа - 8М: Определение момента инерции маятника Максвелла.Скачать  E = T + U = constгде U – потенциальная энергия. В работе в начальный момент времени маятник находится в верхнем положении и обладает потенциальной энергией U . Кинетическая энергия Т = 0 . Когда маятник опустится и пройдет путь h , то потенциальная энергия U 1 = mgh перейдет в кинетическую энергию Т поступательного и вращательного движения Т 2 : U 1 = Т 2 или (2) Так как = V / r , где r – радиус оси, на которую намотаны нити, то уравнение (2) принимает вид: Движение маятника равноускоренное, следовательно, можно применить следующие формулы для пути и скорости: В работе начальная скорость V o = 0, тогда Видео:Маятник и сохранение энергииСкачать  V = atИз этой системы уравнений находим: Подставим полученное значение V в уравнение (3): Эту же формулу можно получить другим способом. На диск массы m действуют сила тяжести mg и натяжений нитей f . Ускорение а центра тяжести диска определяется уравнением: Ось моментов выберем так, чтобы она проходила через центр тяжести диска (т.е. совпадала с его геометрической осью О ). Момент силы тяжести относительно этой оси равен нулю, а момент силы натяжения нитей M = fr , и второй закон Ньютона для вращательного движения маятника имеет вид: Из кинетических соображений легко найти связь между линейным ускорением а и угловым ускорением = d / dt . Так как центр тяжести опускается как раз на столько, на сколько раскручивается нить, то его перемещение h и угол поворота диска связаны соотношением h = r . Дифференцируя это соотношение дважды по времени, получим а = rd / dt , и уравнение (6) можно переписать в виде: Из уравнения (5) найдем: Подставив (7) в (8), получим: Ускорение а найдем из формулы пройденного пути маятника h : a = 2 h / t 2 и подставив в уравнение (7), получим . Это выражение аналогично формуле (4). Поскольку диаметр легче измерить, чем радиус, заменим r на 0,5 d и получим окончательно такую формулу для I o : Здесь I o – момент инерции маятника, m – масса маятника, d – диаметр валика, на который наматываются нити, g – ускорение свободного падения, h – расстояние, пройденное центром маятника за время t . Теперь уточним значение массы m и диаметра d . В данной работе маятник Максвелла представляет собой ось с валиками, на которые плотно насаживается съемное кольцо: где d o – внешний диаметр оси маятника, d н – диаметр нити подвески. Видео:Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать  Практическая часть (эксперимент)Мы знаем, что такое маятник Максвелла и на чём основана его работа. Мы решили изготовить различные маятники, чтобы выяснить от чего зависит их работа. Чтобы узнать, как зависит работа маятника от нити, мы изготовили два одинаковых маятника с нитями, различными по толщине : У маятника с толстой нитью T (период –время, за которое маятник движется сверху вниз и обратно) = 3.6с У маятника с тонкой нитью T= 3.65с Период в нашем случае измерялся с помощью секундомера, измерения приведены сразу с погрешностями. В дальнейшем перед нами ставится задача — усовершенствовать установку таким образом, чтобы во время прохождения крайних точек (верхнего и нижнего) срабатывал датчик времени. Современная лаборатория физики предоставляет такую возможность, т.к. в комплекты многих приборов входит цифровой датчик времени. Вывод: работа маятника не зависит от толщины нити. Также нити различались по длине: l = 46 см, T= 2.5 с l = 92 см, T= 4.6 с Увеличив длину нити в 2 раза, период тоже увеличился примерно в 2 раза. Но необходимо также и учитывать массу нити, что конечно тоже имеет влияние на период. Вывод: период пропорционален длине нити. Чтобы узнать зависит ли работа маятника от стержня, мы изготовили два одинаковых маятника со стержнями, различными по толщине: У маятника, толщина стержня которого = 2см, T= 2.8с У маятника, толщина стержня которого = 2.5см, T= 2с В данном случае стрежни были легкими, незначительная масса. Мы старались подобрать два стрежня равными по длине, разными по диаметру и конечно равными по массе, чтобы данная погрешность не повлияла на ход нашего эксперимента. Вывод: чем тоньше стержень маятника, тем больше период. Так же стержни различались по длине: Вывод: работа маятника не зависит от длины стержня. Чтобы узнать, как зависит работа маятника от диска, мы изготовили два одинаковых маятника, с дисками различными по ширине: У маятника ширина которого = 1 мм, T = 4,5с. У маятника, ширина диска которого = 12мм, T = 5с В 12 раз увеличив ширину, период увеличился незначительно. Вывод: ширина диска не сильно влияет на работу маятника. Так же диски различались по массе: m большая, T= 5.2с m маленькая, T= 5с Разница масс двух маятников была достаточно большая, а период почти не изменился. Вывод: масса диска совсем незначительно влияет на работу маятника. Так же диски имели различный радиус: Мы уменьшили R на 13 и период тоже уменьшился примерно на 13. Вывод: период пропорционален радиусу. Чтобы рассчитать механическую энергию маятника, надо найти его потенциальную и кинетическую энергию из которых она складывается. Потенциальная энергия маятника считается по формуле: E п =mgh Где m(масса маятника) = 0,055кг g(ускорение свободного падения) = 9,81м/с2 h(высота на которую опускается маятник) = 0,21м Где ω=vr –угловая скорость маятника; r(радиус стержня маятника) = 0,0003м; v(скорость опускания центра масс маятника)= 2ht=2 ∙ 0,212,6=0,16м/с; t(время опускания маятника) = 2,6с J–момент инерции маятника, который находится по формуле: Где a=2h/t 2 — ускорение поступательного движения центра масс маятника J=0,055 ∙0,0003 ∙0,0003(9,81 /2,6 ∙2,62 ∙0,21-1) = 0,00000078 Теперь мы можем посчитать кинетическую энергию маятника: Eк= 0,055 ∙ 0,16 ∙0,162 1+ 0,000000780,055 ∙0,003 ∙0,003= 0, 11Дж Теперь легко посчитать механическую энергию нашего маятника: Видео:Маятник МаксвеллаСкачать  ЗаключениеВ ходе проделанной работы по данной теме изучили достаточно большое количество литературы. В работе подробно рассказали про закон сохранения энергии, какие бывают виды энергии, история про маятник Максвелла и принцип его работы. Мы узнали, как на работу маятника влияют все его составные части (длина и толщина стрежня, масса стрежня, его толщина, радиус диска и т.д.). Мы постарались ответили на все вопросы, которые возникали у нас вначале построения этой темы. Но в ходе проведения работы начали возникать новые вопросы: как будет вести себя маятник Максвелла не в газовой атмосфере, а в жидкости? Как преодолеть барьер потерь энергии? Создать магнитный маятник Максвелла. Да, он есть и описан в нашей работе, но если его усовершенствовать и минимализировать потери энергии за счет дргих сил и попробовать его разместить в разных средах. Используя наше современное достижение науки, может все-таки возможно создание вечного двигателя? Об этом стоит подумать. Видео:маятник максвеллаСкачать  ЛитератураВознесенский Н . Н . О машинах вечного движения . М ., 1926 . Ихак — Рубинер Ф . Вечный двигатель . М ., 1922 . Кирпичёв В . Л . Беседы по механике . М . : ГИТЛ , 1951 . Мах Э . Принцип сохранения работы: История и корень его . СПб ., 1909 . Перельман Я . И . Занимательная физика . Кн . 1 и 2 . М . : Наука , 1979 . Савельев И.В. Курс общей физики. Т.1. Механика. Молекулярная физика. – М.: Наука, 1982. Яблонский А.А., Никифорова В.М. Курс теоретической механики. — М.: Высшая школа, 1971. 💡 ВидеоУрок 126. Задачи на закон сохранения энергии (ч.1)Скачать  Физика 10 класс (Урок№13 - Работа. Мощность. Энергия. Закон сохранения механической энергии.)Скачать  Закон сохранения энергии. 9 класс. Решение задачСкачать  Закон сохранения энергии ( шары Ньютона )Скачать  Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать  Превращение одного вида энергии в другой | Физика 7 класс #49 | ИнфоурокСкачать  ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ в механике класс физика ПерышкинСкачать  ЛР "Изменение движения маятника Максвелла"Скачать  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||


 .
.
 =
=  +
+  .
. +
+  +
+  ;
; 

 )
) = 38 см = 0,38 м;
= 38 см = 0,38 м;  = 0,261 кг, R0= 0,004 м – радиус оси;
= 0,261 кг, R0= 0,004 м – радиус оси; , с
, с ,
, 
 ,
, 
 ,
, 
 ,
, 


 , %
, %
 = 2,04
= 2,04  =
=  = 0,1
= 0,1  +
+  +
+  = 0,019 + 0,1+ 0,261 = 0,38 кг;
= 0,019 + 0,1+ 0,261 = 0,38 кг; =
=  =
=  = 0,152 *
= 0,152 *  кг *
кг *  =
=  =
=  = 0,22 *
= 0,22 *  =
=  +
+  = 32,71 *
= 32,71 *  =
=  = (0,41 + 115 + 601) *
= (0,41 + 115 + 601) *  = 2,06
= 2,06  +
+  = 0,3 Дж
= 0,3 Дж * 100 % = 1 %.
* 100 % = 1 %. g —
g — 


 = g —
= g —  = g —
= g —  = g —
= g — 
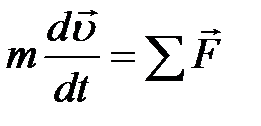 , (4.1)
, (4.1)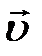 – скорость центра масс,
– скорость центра масс, 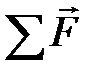 – сумма всех внешних сил, действующих на тело.
– сумма всех внешних сил, действующих на тело.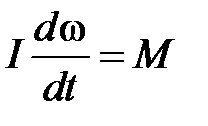 , (4.2)
, (4.2)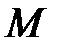 – момент внешних сил относительно той же оси,
– момент внешних сил относительно той же оси, 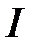 – момент инерции относительно той же оси.
– момент инерции относительно той же оси.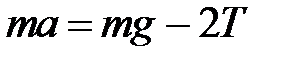 , (4.3)
, (4.3)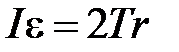 , (4.4)
, (4.4)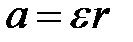 , (4.5)
, (4.5)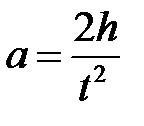 . (4.6)
. (4.6)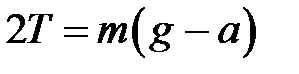 , (4.7)
, (4.7)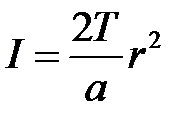 . (4.8)
. (4.8)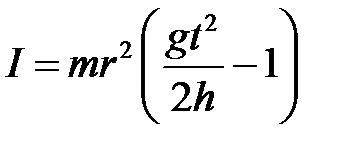 . (4.9)
. (4.9)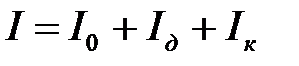 , (4.10)
, (4.10)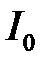 ,
, 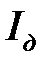 ,
, 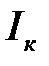 – соответственно моменты инерции оси, диска и кольца маятника.
– соответственно моменты инерции оси, диска и кольца маятника.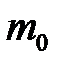 равен
равен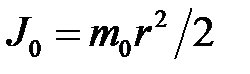 . (4.11)
. (4.11)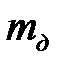 может быть найден по формуле:
может быть найден по формуле: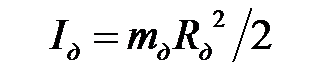 , (4.12)
, (4.12)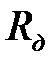 – радиус диска.
– радиус диска.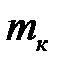 находится по формуле
находится по формуле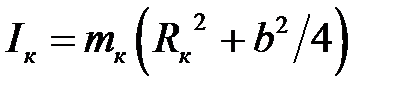 , (4.13)
, (4.13)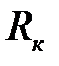 – средний радиус кольца, b – ширина кольца.
– средний радиус кольца, b – ширина кольца.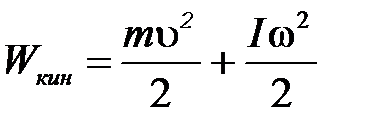 . (4.14)
. (4.14) . (4.15)
. (4.15)




