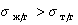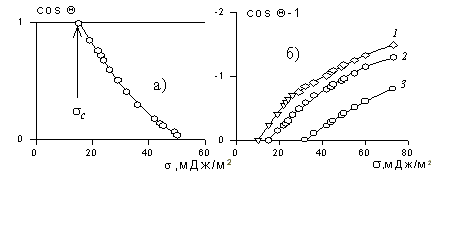Уравнение юнга и его анализ (7 видео)

ГЛАВА ХI. АДГЕЗИЯ, СМАЧИВАНИЕ И РАСТЕКАНИЕ ЖИДКОСТЕЙ

Адгезия и работа адгезии

Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы называют адгезией(прилипанием). Адгезия обеспечивает между двумя телами соединение определенной прочности, обусловленное межмолекулярными силами.

Различают адгезию между двумя жидкостями, между жидкостью и твердым телом и между двумя твердыми телами.

Явления адгезии и смачивания широко распространены. Склеивание материалов, нанесение покрытий, получение материалов на основе связующих и наполнителей (бетон, резина, стеклопластики и т. п.), сварка и паяние металлов, печатание – все эти процессы связаны с адгезией и смачиванием, которые в значительной степени определяют качество материалов и изделий.

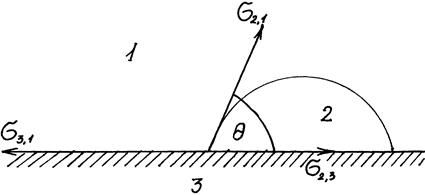
Рис.27. К выводу соотношения между работой адгезии и поверхностными натяжениями взаимодействующих компонентов (уравнения Дюпре): 1 – газ; 2 – жидкость; 3 ‑ твердое тело

Из-за сложности протекающих процессов, рассматриваемые в данном разделе межфазные явления до сих пор недостаточно изучены. Поэтому основное внимание будет уделено системам, в которых имеется хотя бы одна жидкая фаза, что позволяет обеспечивать равновесные обратимые условия и соответственно использовать термодинамические соотношения.

Адгезия – результат стремления системы к уменьшению поверхностной энергии. Поэтому адгезия является самопроизвольным процессом.

Работа адгезии W_ад (по аналогии с работой когезии) определяется как работа изотермического обратимого разделения двух конденсированных фаз вдоль межфазной поверхности единичной площади.

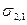
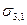
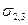
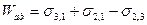
При таком разделении образуются свободные поверхности раздела обеих конденсированных фаз с газом, имеющие энергии и , и исчезает межфазная поверхность с энергией (рис.27), следовательно,

(XI.1)

Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии. Из него следует, что работа адгезии тем больше, чем больше поверхностные натяжения исходных компонентов и чем меньше межфазное натяжение.

Величина W_ад характеризует родственность контактирующих фаз, т. е. степень насыщения нескомпенсированных поверхностных сил при контакте. Межфазная энергия 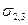, наоборот, определяет интенсивность остаточных нескомпенсированных сил на границе раздела конденсированных фаз.

Она измеряется в тех же единицах, что и поверхностное натяжение (Дж/м 2 ).

Работу адгезии экспериментально определяют при непосредственном разрушении соединения. Работу адгезии можно определить и косвенными методами, которые особенно удобны, если хотя бы одной из взаимодействующих фаз является жидкость и можно измерить, например, краевой угол.

Смачивание и краевой угол. Закон Юнга

Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом).

Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).

При нанесении небольшого количества жидкости, например, капли на поверхность другой жидкости, имеющей большую плотность, или на поверхность твёрдого тела можно наблюдать два процесса, если приводимые в контакт вещества взаимно нерастворимы. В одном случае нанесенная жидкость остается на поверхности другой фазы в виде капли, принявшей при установившемся равновесии определенную форму. В другом случае капля растекается по поверхности. Вначале рассмотрим первый процесс, когда капля не растекается полностью по поверхности другого тела.

Рис.28. К выводу уравнения для краевого угла (закона Юнга).

Рис.28 иллюстрирует состояние капли жидкости на поверхности твёрдого тела в условиях равновесия. Поверхностная энергия твёрдого тела, стремясь уменьшиться, вызывает растяжение капли по поверхности. Эта энергия равна поверхностному натяжению твёрдого тела на границе с воздухом s_{3, 1}. Межфазная энергия на границе твёрдого тела с жидкостью s_{2, 3} стремится, наоборот, сжать каплю, т. е. поверхностная энергия уменьшается за счет снижения площади поверхности. Растеканию препятствуют когезионные силы, действующие внутри капли. Действие когезионных сил направлено от границы между твёрдой, жидкой и газообразной фазами по касательной к сферической поверхности капли и равно s_{2, 1} (силы гравитации не учитываются). Угол q, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом смачивания.

Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:

(XI.2)

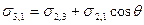
Полученное соотношение называется законом Юнга. Отсюда количественную характеристику смачивания – косинус краевого угла можно выразить через поверхностные и межфазное натяжения:

(XI.3)

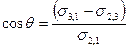
Чем меньше угол q и соответственно больше cos q, тем лучше смачивается поверхность. При остром угле q, т. е. при cos q > 0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол q тупой, т. е. cos q

Содержание

2.3.2. Смачивание и растекание на границе твердое тело – жидкость – газ
Лекция №4
План лекции:
МЕЖФАЗНЫЕ ВЗАИМОДЕЙСТВИЯ МЕЖДУ КОНДЕНСИРОВАННЫМИ ФАЗАМИ
АДГЕЗИЯ
Cоотношение между Wa и s :
Механизм адгезии
СМАЧИВАНИЕ
РАСТЕКАНИЕ
💥 Видео

Видео:Почему Карл Юнг гений психологии? Аналитическая теория. АрхетипыСкачать

2.3.2. Смачивание и растекание на границе твердое тело – жидкость – газ

В большинстве случаев жидкость на поверхности твердого тела остается в виде капли, большей или меньшей толщины, контактирующей с твердым телом под определенным углом, который называется краевым углом смачивания и обозначается буквой Q (рис. 1.24). Растекание капли по поверхности прекратится при достижении равновесия, которое без учета сил тяжести может быть описано уравнением Юнга:

(1.2.44)

, (1.2.45)

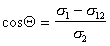
где индексы 1, 2, 3 – обозначают, соответственно, твердую, жидкую и газовую фазы.

Работа адгезии выражается уравнением Дюпре:

(1.2.46)

. (1.2.47)

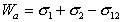
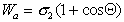
Рис. 1.24. Капля жидкости на поверхности твердого тела (схема)

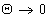
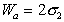
Работа адгезии при ,т.е. при полном смачивании, , что эквивалентно работе когезии жидкости. Если Q = 180 o , соs Q = -1 и в соответствии с уравнением (1.2.47) W_a = 0, т.е. жидкость не смачивает твердую поверхность. При Q» 90 o жидкость проявляет слабое смачивание.

Следует помнить, что определение работы адгезии в реальных системах предполагает равновесие фаз, насыщенных относительно друг друга.

Кроме того, твердая поверхность, по которой происходит растекание жидкости, не свободна. Она обычно покрыта пленкой вещества, адсорбированного из газо-паровой фазы. Эта пленка имеет поверхностное давление p, поэтому

, (1.2.48)

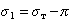
Смачивание неоднородных, пористых или шероховатых поверхностей сопровождается запиранием пузырьков воздуха в неровностях. В результате этого краевые углы смачивания сухой и предварительно увлажненной поверхностей различаются. Такое явление носит название «гистерезис смачивания». Гистерезис смачивания проявляется также при загрязнении поверхности, в результате чего она становится неоднородной при закреплении на ней твердых частиц или жировых пленок. В этом случае поверхность ведет себя как составная.

Шероховатость поверхности учитывается введением коэффициента шероховатости r, представляющего отношение площади поверхности реального тела к площади идеально гладкой поверхности, тогда

. (1.2.49)

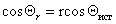
Можно отметить, что если краевой угол смачивания гладкой поверхности, например полимерной пленки, меньше 90 o , то шероховатость (ткань из волокон этого полимера) уменьшает его, если же он больше 90 o , то шероховатость его увеличивает. Для составной поверхности, которая специфична для большинства текстильных материалов, наличие участков различной природы может быть учтено введением коэффициентов x, характеризующих долю поверхности с различными свойствами. Например, если текстильный материал изготовлен из волокон двух видов 1 и 2, то

. (1.2.50)

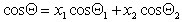
Если переплетение нитей таково, что получается сетчатый или дырчатый материал, то уравнение (2.50) принимает вид

, (1.2.50′)

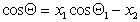
где х₂ – доля открытой поверхности.

Как мы обсуждали выше, поверхностное натяжение можно разделить на компоненты дисперсионных и полярных сил, а при нахождении межфазового натяжения для многих жидких границ можно ограничиться лишь дисперсионной составляющей. Такое ограничение позволяет провести обсуждение явления смачивания (по крайней мере, низкоэнергетических поверхностей, к каковым можно отнести подавляющее большинство волокнообразующих полимеров), в рамках теории дисперсионных сил.

Как показал Н. В. Чураев смачивание неполярной жидкостью твердой поверхности возможно, если будет соблюдаться условие смачивания, которое выражается уравнением

, (1.2.51)

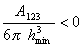
где А₁₂₃ – составная постоянная Гамакера при взаимодействии жидкости (фаза 2) с твердым телом (фаза 1) на границе с воздухом (фаза 3); h_m_in — наименьшая толщина пленки, которая фактически соответствует Ван-дер-Ваальсову расстоянию, т.е. h_m_in = (0,22¸0,24) нм. Например, для воды на поверхности тефлона А₁₂₃ = -7·10 — 21 Дж.

Учет только дисперсионных сил приводит к уравнению

, (1.2.52)

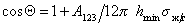
При расчетах углов смачивания твердых поверхностей следует учитывать поверхностное давление пленки, образованной при адсорбции из газо-паровой фазы. Тогда с учетом уравнения (1.2.48), уравнение Юнга (1.2.45) следует записать в виде

. (1.2.53)

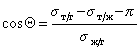
Способ расчета поверхностного давления предложили Бэнгхэм и Разорук:

, (1.2.54)

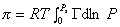
где P – равновесное давление, Г– равновесная адсорбция газа (пара), P_s – давление насыщения.

При больших углах смачивания и слабом взаимодействии жидкости с твердым телом поверхностное давление обычно не учитывают.

Для неполярных жидкостей на низкоэнергетической поверхности твердого тела для работы адгезии было получено выражение

. (1.2.55)

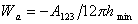
Поэтому уравнение Дюпре (1.2.46) можно записать

. (1.2.55′)

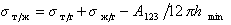
Для дисперсионной составляющей жидкости

, (1.2.56)

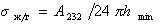
где А₂₃₂ – постоянная Гамакера взаимодействия жидкости через прослойку газа (пара).

Сочетая уравнения (1.2.47), (1.2.55) и (1.2.56), получаем

. (1.2.57)

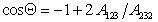
Очевидно, что Q = 0, т.е. при полном смачивании, cosQ = 1, если

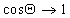
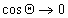
Уравнение (1.2.57) позволяет прогнозировать вероятность смачивания () или наоборот — несмачивания () жидкостью поверхности твердого тела по известным постоянным межмолекулярных сил взаимодействия.

Чаще, однако, прибегают к определению постоянной Гамакера по известному значению межфазового натяжения на границе «твердое тело — газ». Эту характеристику поверхности твердого тела находят при распространении подхода Джирифалько и Гуда, рассмотренного нами выше для границы двух жидкостей, на поверхность раздела «жидкость — твердое тело», уравнения (1.2.23), (1.2.35).

Так приложение уравнения (1.2.34) к уравнению Юнга для случая смачивания неполярной жидкостью поверхности полимерного материала позволяет получить уравнение, известное как уравнение Фоукса, при

. (1.2.58)

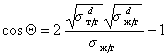
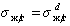
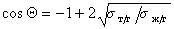
Если жидкости неполярны и , то уравнение (1.2.58) переходит в уравнение

. (1.2.59)

Уравнение (1.2.59) Зисман предложил использовать для определения поверхностного натяжения твердых тел. Очевидно, что при 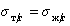cosQ =1, а угол смачивания будет равен нулю (Q = 0), т.е. наступает полное смачивание.

Естественно, что метод Зисмана ограничен некоторыми условиями, в частности, из уравнения (1.2.57) следует, что полное смачивание возможно при дисперсионной неразличимости твердого тела и жидкости, т.е. при А₂₃₂= А₁₂₃.

В действительности такого условия никогда невозможно достигнуть хотя бы потому, что если жидкость и твердое тело будут иметь одинаковый химический состав, их постоянные Гамакера будут различаться из-за различий в плотности.

Другое ограничение, связанное с применением метода Зисмана, основано на том, что использовать для измерения краевых углов смачивания следует лишь неполярные жидкости. Наиболее целесообразно применять гомологические ряды жидкостей. При величине поверхностного натяжения жидкостей более 35 мДж/м 2 метод Зисмана уже дает высокую погрешность, так как необходимо учитывать вклад полярных сил, которые в отличие от дисперсионной составляющей могут иметь и отрицательное значение. С другой стороны, приложение для смачивания твердых тел полярными жидкостями уравнения Ву (1.2.36) позволяет рассчитать полярную составляющую поверхностного натяжения жидкости, если для одной из неполярных жидкостей измерить краевой угол смачивания. Для расчета используют уравнение

Рис. 1.25. Зависимость смачивания поверхностей от поверхностного натяжения жидкостей. Материал поверхности: 1- FC-721; 2- ПТФЭ (тефлон); 3 — полиэтилен

. (1.2.60)

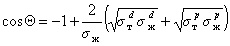
Этот метод позволил разделить величину поверхностного натяжения жидкостей на полярную и дисперсионную компоненты и определить поверхностное натяжение многих волокнообразующих полимеров.

Пример зависимости косинуса угла смачивания поверхности пленок различными жидкостями приведен на рис.1.25. Для описания этих зависимостей Зисман предложил использовать эмпирическое уравнение

, (1.2.61)

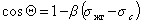
где bэмпирическая постоянная, s_с – «критическое» поверхностное натяжение твердого тела, при котором происходит полное смачивание твердого тела жидкостью. Очевидно, что cos Q =1 при условии s_жг = s_с .

Как мы обсуждали выше, этот критерий в известной мере является условным, хотя и отражает энергетическое состояние поверхности твердого тела.

Реальное значение поверхностного натяжения твердого тела экспериментально определить невозможно, также как и рассчитать его теоретически. В этой связи метод Зисмана нашел широкое применение в практике исследования полимерных материалов, а также полимерных покрытий тканей, используемых в качестве отделочных материалов

Видео:Аналитическая психология Карла Юнга. Курс. Часть IСкачать

Лекция №4

План лекции:

Видео:Как управлять тёмной стороной | Практика Карла Юнга по интеграции тениСкачать

МЕЖФАЗНЫЕ ВЗАИМОДЕЙСТВИЯ МЕЖДУ КОНДЕНСИРОВАННЫМИ ФАЗАМИ

К межфазным взаимодействиям между конденсированными фазами относятся смачивание, растекание и адгезия.

Как правило, адгезия и смачивание сопровождают друг друга. Эти явления широко распространены в природе и в различных отраслях промышленности (нанесение лакокрасочных покрытий, получение материалов на основе связующих и наполнителей — бетон, резина и т. д.)

Видео:Что такое бессознательное | Сумасшедшие версии Карла Юнга и БуддыСкачать

АДГЕЗИЯ

Адгезия — межфазное взаимодействие, или взаимодействие между приведёнными в контакт поверхностями конденсированных тел разной природы (прилипание). Адгезия обеспечивает между двумя телами соединение определенной прочности, обусловленное межмолекулярными силами.

Адгезия между — ж/ж, ж/т, т/т.

Адгезия — результат стремления системы к уменьшению поверхностной энергии, поэтому это самопроизвольный процесс. Работа адгезии W_a, характеризующая прочность адгезионной связи, определяется работой обратного разрыва адгезионной связи, отнесённой к единице площади:

W _s = W_аS, где W_s — полная работа адгезии (4.1)

Cоотношение между W_a и s :

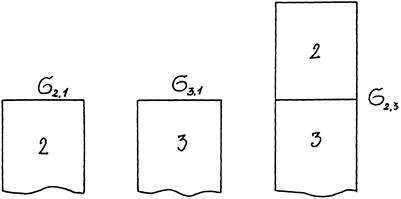
Предположим, что имеется контакт между 3 фазами — 1 — газ, 2 -жидкость, 3 — твердое тело, 2, 3 — конденсированные фазы. Введем следующие обозначения поверхностных натяжений:

s _2,3 — поверхностное натяжение на границе раздела двух конденсированных фаз

s _2,1 и s _3,1 — поверхностное натяжение на границе с воздухом

Уравнение Дюпре отражает закон сохранения энергии при адгезии. Из него следует, что работа адгезии тем больше, чем больше поверхностные натяжения исходных компонентов и чем меньше конечное межфазное натяжение.

Уравнение 4.2 справедливо только для изобарно-изотермического процесса в отсутствии электрического и химического взаимодействия между контактирующими телами, его используют только для определения равновесной работы адгезии жидкости.

Равновесную работу адгезии можно сопоставить с равновесной работой когезии. Когезия — определяет связь между молекулами внутри тела и в пределах одной фазы, характеризует прочность конденсированных тел и их способность противодействовать внешнему усилию.

Механизм адгезии

Первая стадия — транспортная, перемещение адгезива (клеящего вещества) к поверхности субстрата (тело, на которое наносят адгезив) и их определенное ориентирование в межфазном слое.

Вторая стадия — взаимодействие адгезива и субстрата, обусловлено различными силами (от ван-дер-ваальсовых до химических).

Завершается процесс адгезии межмолекулярным взаимодействием контактирующих фаз, что соответствует минимальной поверхностной энергии. Различают несколько механизмов (и, соответственно, теорий) в зависимости от природы взаимодействующих тел и условий, при которых происходит адгезия.

1.Механическая адгезия — осуществляется путем затекания в поры и трещины поверхности твердого тела жидкого адгезива., который потом затвердевает, обеспечивая механическое зацепление.

2.Молекулярная (адсорбционная) адгезия — возникает под действием межмолекулярных ван-дер-ваальсовых сил и водородных связей.

3.Электрическая теория — связана с образованием ДЭС на границе раздела между адгезивом и субстратом.

4.Диффузионный механизм — предусматривает взаимное проникновение молекул и атомов в поверхностные слои взаимодействующих фаз.

Чаще всего механизм адгезии является смешанным.

Теоретическая оценка адгезии очень приближённа, т. е., механизм её недостаточно изучен.

Видео:Карл Густав ЮНГ Психологические типы 1/3Скачать

СМАЧИВАНИЕ

Смачивание — это поверхностное явление, заключающееся во взаимодействии жидкости с твёрдым или другим жидким телом при наличии контакта трех несмачивающихся фаз, одна из которых воздух.

Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания) или просто краевым углом (углом смачивания).

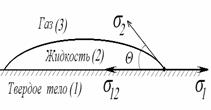
Рис.4.2. К выводу уравнения для краевого угла (закон Юнга).

Рис.4.2. иллюстрирует состояние капли жидкости на поверхности твердого тела в условиях равновесия. Поверхностная энергия твердого тела, стремясь уменьшиться, вызывает растяжение капли по поверхности. Эта энергия равна поверхностному натяжению твердого тела на границе с воздухом s _3,1 .Межфазная энергия на границе твердого тела с жидкостью s _2,3 стремится сжать каплю. Растеканию препятствуют когезионные силы, действующие внутри капли. Действие когезионных сил направлено от границы между твердой, жидкой и газообразной фазами по касательной к сферической поверхности капли и равно s _2,1 .Угол q — краевой угол или угол смачивания.

Чем меньше краевой угол , тем лучше смачивание поверхности.

Если cos( q )>0 , то поверхность хорошо смачиваемая, cos( q )

Если разность s _3,1 — s _2,3 в уравнении Дюпре заменить её выражением из закона Юнга, то

W_a/ s _2,1 = 1+ cos( q ) — уравнение Дюпре-Юнга (4.5)

4.3, 4.4, 4.5 — только для идеально гладких тел. На поверхности реальных тел есть поры, трещины, и т. д.

Рассмотрим кинетический катерезис, который замедляет достижение равновесной формы капли.

Рис.4.3.Статические углы натекания и оттекания.

Для реальных тел: равновесный угол смачивания равен полусумме предельных углов натекания и оттекания:

cos( q ) = (cos( q _нт ) + сos( q _от ))/2 (4.6)

Влияние шероховатости на кривой угол:

k = cos( q _ш )/cos( q ) , где к — коэфф. шероховатости

При повышении степени шероховатости смачиваемость улучшается.

Видео:Карл Юнг. Бог, коллективное бессознательное и Гитлер.Скачать

РАСТЕКАНИЕ

Капля жидкости, нанесенная на поверхность, может оставаться на ее определенном участке, и система будет находится в равновесии в соответствии с законом Юнга, или же растекаться по поверхности. В обоих случаях система переходит в состояние с минимальной энергией Гиббса.

Из этого соотношения следует, что уменьшение межфазного натяжения s _2,3 (увеличение работы адгезии) и поверхностного натяжения жидкости s _2,1 , способствует растеканию жидкости.

Растекание происходит в том случае, если работа адгезии превышает работу когезии.

Способность жидкости растекаться зависит от когезии наносимых на поверхность жидкостей.

С повышением температуры увеличивается работа адгезии, поэтому нерастекающаяся жидкость с увеличением температуры может начать растекаться.