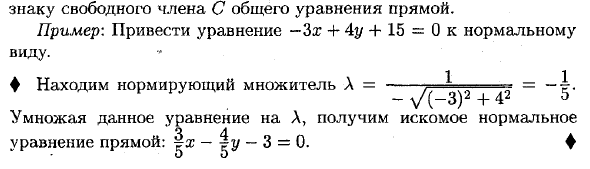Уравнение y kx b определяет на плоскости в декартовой системе координат некоторую (3 видео)

Содержание

ПРЯМАЯ И ПЛОСКОСТЬ
9.1. Прямая на плоскости
Общее уравнение прямой: описание, примеры, решение задач
Общее уравнение прямой: основные сведения
Неполное уравнение общей прямой
Общее уравнение прямой, проходящей через заданную точку плоскости
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Составление общего уравнения прямой
Различные виды уравнений прямой на плоскости
Различные виды уравнений прямой на плоскости
📺 Видео

Видео:Вариант 51, № 7. Нахождение k и b линейной функции y=kx+b. Пример 1Скачать

ПРЯМАЯ И ПЛОСКОСТЬ

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

9.1. Прямая на плоскости

Понятие прямой является одним из фундаментальных понятий геометрии. Прямая определяется следующим образом: это линия наименьшей длины, соединяющая две точки. Уравнение у = кх + b определяет на плоскости в декартовой системе координат некоторую прямую. Чертеж на рис. 9.1 показывает, что геометрический смысл коэффициентов к и b следующий: а — tg(p, где ф — угол наклона прямой, отсчитываемый от положительного направления оси ОХ против часовой стрелки; b — длина отрезка, заключенного между началом координат и точкой пересечения оси OY с прямой.

Рис. 9.1. Прямая на плоскости

Это же уравнение можно записать в другом виде. Пусть , У_х) —

координаты точки А, а (х₂, у₂) — координаты точки В. Проведем через эти две точки прямую. Легко показать, что уравнение этой прямой имеет следующий вид: У

У_Х = к(х-х₁). Отсюда, используя определение тангенса, получаем так называемое каноническое уравнение прямой:

Рассмотрим еще одну форму записи уравнения прямой:

При В ф О получаем уравнение у = (А /В)х + (С/В).

Пусть теперь А, В, С ф 0. Тогда можно получить уравнение

где

Легко показать, что эта прямая проходит через точки с координатами (0, Ь) и (а, 0). Поэтому уравнение (9.3) называется уравнением в отрезках.

Рассмотрим теперь следующую задачу: написать уравнение прямой, проходящей через точку, определяемую радиус-вектором го и перпендикулярную вектору п.

Пусть г — произвольный радиус-вектор (рис. 9.2).

Рис. 9.2. К векторному определению прямой

Рис. 9.3. Вьюод уравнения

Разность г — го лежит на нашей прямой и, очевидно, перпендикулярна вектору п. Отсюда получаем уравнение прямой

или (г, п) — (го, n) — const.

В дальнейшем будем считать, что |n| = 1.

Подставим теперь в уравнение (9.4) координаты произвольной точки, не лежащей на прямой. Пусть ее радиус-вектор есть г’. Тогда: г’ — i*o = г», где г» — вектор, соединяющий точку А(г’) с точкой М(го). Разложим вектор г»(см. рис. 9.3) на две составляющие: Гь перпендикулярный п, и г₂||п; г» = П + г₂.

Поскольку г₂||п, то r₂= d_n, где |d| расстояние от точки А до прямой.

Таким образом, (9.3) удобно для нахождения расстояния от точки до прямой.

Преобразуем это уравнение к виду, удобному для вычислений.

Нормальный вектор можно записать в виде n = (costp, sin(p). Тогда (9.3) преобразуется к виду

Или

Расстояние от произвольной точки A(x’,y t ) до прямой равно

Уравнение Ах + By +С — 0 приводится к виду (9.5) делением на Оно называется нормальным, или нормированным уравнением прямой.

Если задано уравнение прямой в общей форме, т.е.

то легко показать, что вектор п = (А, В) перпендикулярен этой прямой.

Если заданы две прямые

Ах + Ву + С = 0и А’х + В’у +С = 0, (9.8)

то они перпендикулярны, если перпендикулярны их нормальные векторы, т.е. векторы п = (А, В) и п 1 = (А’, В). Следовательно, прямые (9.8) перпендикулярны АА’ + ВВ’=0.

Видео:Занятие 1. График линейной функции y=kx+bСкачать

Общее уравнение прямой: описание, примеры, решение задач

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Видео:ЛИНЕЙНАЯ ФУНКЦИЯ | 7 класс Макарычев | график функции y=kx+bСкачать

Общее уравнение прямой: основные сведения

Пусть на плоскости задана прямоугольная система координат O x y .

Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .

указанная теорема состоит из двух пунктов, докажем каждый из них.

Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.

Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .

Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.

Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.

Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .

Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .

Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0

Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .

Рассмотрим конкретный пример общего уравнения прямой.

Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Видео:ГРАФИК ФУНКЦИИ y = kx + b | линейная функция | 7 классСкачать

Неполное уравнение общей прямой

Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.

Разберем все вариации неполного общего уравнения прямой.

Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.

Решение

Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:

Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0

Ответ: 7 x — 2 = 0

На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .

Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .

Ответ: y — 3 = 0 .

Видео:Алгебра 8 класс (Урок№3 - График функции y=kx)Скачать

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.

Решение

Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0

Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:

A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0

Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .

Ответ: x — 2 · y + 11 = 0 .

Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:

2 3 x 0 — y 0 — 1 2 = 0

Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2

Ответ: — 5 2

Видео:Задание 5 Знаки коэффициентов k и b в формуле линейной функции y=kx+bСкачать

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .

Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .

Это равенство возможно записать как пропорцию: x + C A — B = y A .

В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .

Перепишем равенство в виде пропорции: x — B = y + C B A .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.

Решение

Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .

Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.

Ответ: x — 3 = y — 4 3 0 .

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.

Решение

Осуществим переход от общего уравнения к каноническому:

2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Теперь примем обе части полученного канонического уравнения равными λ , тогда:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .

Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение

Произведем нужные действия по алгоритму:

2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x

Ответ: y = — 2 7 x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.

Решение

Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Ответ: x — 1 2 + y 1 14 = 1 .

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0

Каноническое уравнение преобразуется к общему по следующей схеме:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0

Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.

Решение

Осуществим переход от параметрических уравнений к каноническому:

x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0

Перейдем от канонического к общему:

x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0

Ответ: y — 4 = 0

Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.

Решение:

Просто перепишем уравнение в необходимом виде:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0

Ответ: 1 3 x + 2 y — 1 = 0 .

Видео:ЕГЭ задание 9 Функции y=k|x|+b и y=|kx+b|Скачать

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение

Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0

Ответ: 2 x — 3 y — 5 = 0 .

Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .

Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0

Видео:19 Функция y=kx+b и ее графикСкачать

Различные виды уравнений прямой на плоскости

Видео:Линейная функция и её график. Алгебра, 7 классСкачать

Различные виды уравнений прямой на плоскости

Различные типы уравнений, действующих непосредственно на плоскости Самая простая линия — это прямая линия. Различные способы определения прямых соответствуют различным типам уравнений в декартовых системах координат. 1. Линейное уравнение с угловым коэффициентом Дает произвольную прямую линию на плоскости Ohu, которая не параллельна оси Oy. Его положение полностью определяется ординатой b пересечения N (Q; b) с осью Oy и углом a между осью Oh и линией. Под углом o; (0 ^ a Людмила Фирмаль

Знак свободного члена C общего уравнения для прямой. Пример: приведите уравнение -3x-b 4y + 15 = 0 к стандартной форме. ♦ Коэффициент нормализации Л = — ^ Д3 ^ 2 + 42 = Умножьте это уравнение на A, чтобы получить желаемое нормальное уравнение для линии. — 3 = 0.Это удовлетворяется координатами любой точки M (x; y) на прямой.

Вы можете видеть, что любая точка P (x; y) Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Не существует В этом случае линейное уравнение имеет вид х = а, (2) Где а — абсцисса пересечения линии и оси Ox. Обратите внимание, что уравнения (1) и (2) являются линейными уравнениями. 2. Общее уравнение прямой Рассмотрим уравнение первого порядка относительно общего вида x и y. Ax + By + C = 0, (3) Где A, B и C — произвольные числа, а A и B — одновременно ненулевые. Уравнение (3) указывает, что это линейное уравнение. Есть два случая. Если B = 0, форма уравнения (3) имеет вид Ax + C = 0, AΦ0, т.е. x = -Это линейное уравнение, параллельное оси Oy и проходящее через точку В случае ΦΦ0 y =-получается из уравнения (3).

Это линейное уравнение с угловым коэффициентом k = tgc * = -. Некоторые частные случаи общего уравнения прямой: 1) Если A = 0, уравнение сводится к виду y =. Это линейное уравнение, параллельное оси Ox 2) Когда B = 0, линия параллельна оси Oy. 3) Если C = 0, получить Ax + By = 0. Координаты точки 0 (0; 0) удовлетворяют уравнению, и линия проходит через начало координат.

Следовательно, уравнение (3) является линейным уравнением и называется общим линейным уравнением. Людмила Фирмаль

Линейное уравнение через заданную точку В этом направлении Сделайте так, чтобы линия проходила через точку M (x0; y0), и ее направление характеризуется угловым коэффициентом k. Уравнение для этой линии можно записать в виде y = kx 4-6. Поскольку прямая проходит через точку M (x0, y0), координаты точки удовлетворяют уравнению линии y0 = kx o + b.

Следовательно, 6 = уо-кхо. Подставляя значение b в выражение y = kx + b, получаем искомое выражение для строки y = kx + yo-kx0. у-йо = к (х-хо). (4) Уравнение (4) с различными значениями k также называется уравнением пучка вокруг точки M (x0 ‘, Y0). • Из этого карандаша невозможно определить только прямые линии, параллельные оси Oy. 4. Уравнение прямой, проходящей через две точки Пусть прямая проходит через точки M (x y ) и M2 (x2 ‘, Y2). Форма уравнения для прямой, проходящей через точку Mb: Y

2 / i = k (x-zi), (5) Где k — неизвестный коэффициент Поскольку прямая проходит через точку M2 (^ 22/2)>, координаты этой точки должны удовлетворять уравнению (5): Y2-Y1- = k (x2-x1).

Найти k = ^ отсюда — заменить найденное X2-X Получите уравнение для прямой, которая проходит через значения k, точек M и M ^ в уравнении (5). L = (б) 2 / 2-2 / 1- Для этого уравнения Xi × X2, Y Φy-X2 = xi прямая, проходящая через точки M yi) и M2 (x2] Y2), предполагается параллельной оси ординат. Форма уравнения: х = х . Если y2 = 2 / s, уравнение линии можно записать в виде y = y / i. Линия M-yM2 параллельна горизонтальной оси.

Уравнение отрезка Линия пересекает ось Ox в точке M (a; 0) и ось Oy в точке Mg (0; b). В этом случае уравнение (6) принимает следующий вид: U- 0 Это 6-0 0-а ‘ Это уравнение называется линейным сегментным уравнением. Это связано с тем, что числа a и b указывают, какой отрезок отрезает линия по координатным осям. , х-а Х у

+ I = L a b в Mg (0; 6) б ИЛИ ®

Уравнение прямой через заданную точку, перпендикулярную этому вектору Найти линейное уравнение через заданную точку M0 (x0 y0), перпендикулярную данному ненулевому вектору n = (A; B). Возьмем произвольную точку M (x; y) на прямой и рассмотрим вектор M0M- (x-x0; Y-Yo). • Векторы n и McM являются вертикальными, поэтому их скалярное произведение равно нулю. A (x-x0) + B (y-yo) = 0. (7) Уравнение (7) называется уравнением прямой, проходящей через данную точку, перпендикулярную данному вектору и y. Вектор ri = (A) B), перпендикулярный прямой, называется вектором нормали этой прямой.

Уравнение (7) можно переписать в следующем формате Ax + By + C = 0, (8) Где A и B — координаты нормального вектора, а C = —Aho — W / o — свободный член. Уравнение (8) является общим уравнением для линии (см. (3)). 7. Полярные координатные уравнения для прямых Найти линейные уравнения в полярных координатах. Его положение может быть определено путем указания расстояния p от полюса O до конкретной линии и угла a между полюсом OP и осью I через полюс O, перпендикулярный этой линии. Для любой точки M (r;

с другой стороны, pR / OM = OM cos (a-

Следовательно, линейное уравнение (9) в декартовой системе координат принимает вид: x-cosо4-у • sinа-р = 0. (10) Уравнение (10) называется линейным нормальным уравнением. 44 года п / / a x о Вот как можно сделать уравнение (3) прямой в виде (10). Умножим все слагаемые в уравнении (3) на некоторый коэффициент, чтобы получить Л ^ ОХЛх + ХВу + АС = 0. Это уравнение становится уравнением (10). В результате должно быть выполнено уравнение: A / 4 = cos a-, XB = sin a, A C = -p. Из первых двух уравнений найдите Л2А2 + A2J52 = cos2 a + sin2а, т.е. А = ±> * y / A2 + B’2 Х называется нормировочным фактором. Согласно третьему уравнению АС = -р, знак нормировочного коэффициента меняется на противоположный