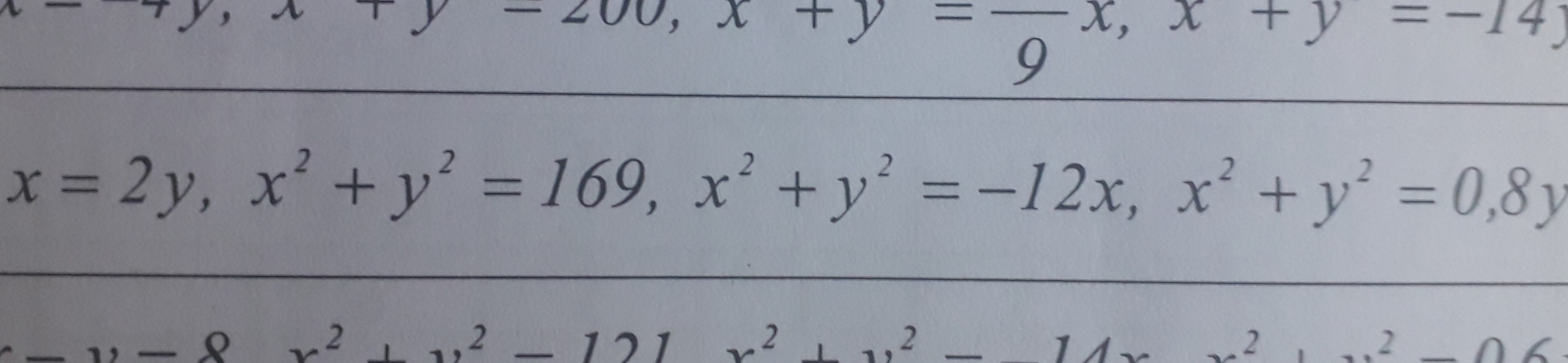Условие
Записать уравнения кривых в полярных координатах и построить их. 
Решение
Вводим полярные координаты
x=r*cos φ
y=r*sin φ
1)
x=2y
r*cos φ=2r*sinφ ⇒ tgφ=2 — уравнение линии в полярных координатах
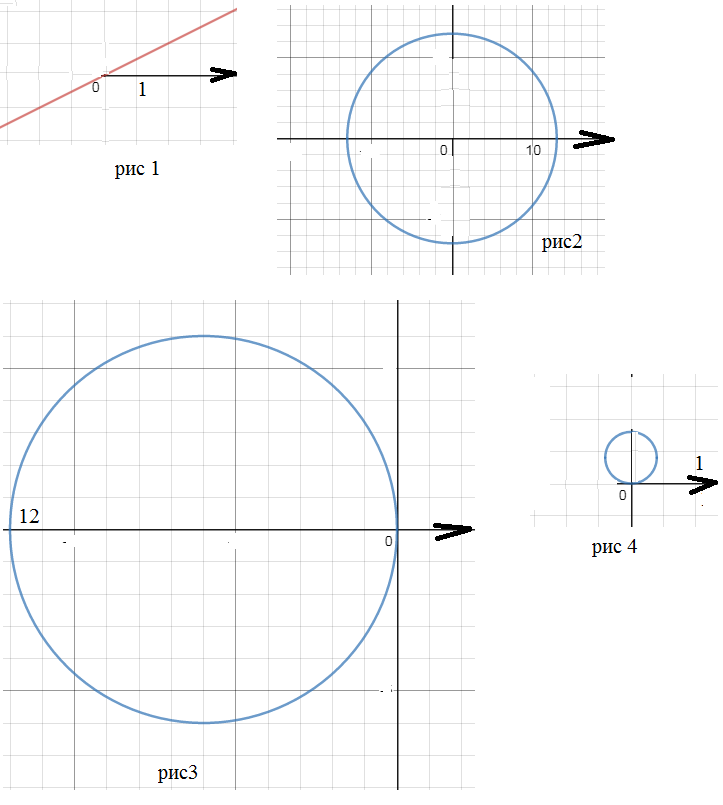
Луч под углом φ к полярной оси, причем tgφ =2
(r*cos φ)^2+(r*sinx φ)^2=169
r^2*(cos^2 φ +sin^2 φ )=13
r=13 — уравнение линии в полярных координатаx
Окружность с центром в точке О радиусом r=13
(r*cos φ)^2+(r*sinx φ)^2=-12*r*cosφ
r^2*(cos^2 φ +sin^2 φ )=-12*r*cosφ
так как r ≥ 0 ⇒ -12cosφ ≥ 0 ⇒ cos φ ≤ 0
Окружность в 2 и 3 четверти
(r*cos φ)^2+(r*sinx φ)^2=0,8*r*sinφ
r^2*(cos^2 φ +sin^2 φ )=0,8*rsinφ
так как r ≥ 0 ⇒ 0,8*sinφ ≥ 0 ⇒ sin φ ≥ 0
Окружность в 1 и 2 четверти
Уравнения для различных видов кривых.
Лемниската Бернулли, плоская алгебраическая кривая, в прямоугольных координатах описывается уравнением:
(х 2 + у 2 ) 2 = 2с 2 (х 2 — у 2 ),
в полярной:
Причем, 2с — расстояние между фокусами, размещены они на оси 0х, и начало координат пополам разделяет отрезок между ними.
Роза – плоская кривая, напоминающее символическое изображение цветка. Данная кривая представлена уравнением в полярных координатах:
Причем коэффициент k определяет количество лепестков.
Улитка Паскаля – плоская кривая представленная выражениями:
l — расстояние, на которое смещается точка вдоль радиус — вектора.
Полукубическая парабола – плоская алгебраическая кривая, характеризующаяся выражением y 2 = ax 3 в прямоугольной системе координат.
Астроида – уравнение в декартовых координатах имеет вид:
Кардиоида. Если а — радиус окружностей, начало координат находится в крайней правой точке горизонтального диаметра неподвижной окружности. Тогда уравнения кардиоиды принимает вид:
в прямоугольных координатах — (х 2 + у 2 +2аx) 2 – 4a 2 (х 2 + у 2 ) = 0;
Спираль Архимеда – спираль, плоская кривая, траектория точки М, которая равномерно движется вдоль ОV с началом в О, в то время как сам луч ОV равномерно вращается вокруг О.
Уравнение Архимедовой спирали в полярной системе координат:
где k — смещение точки M по лучу r, при повороте на угол равный одному радиану.
Циклоида — плоская трансцендентная кривая. Характеризуется в декартовых координатах так:
.
Дано уравнение линии (х2 + у2)2 = 4ху. В полярных координатах оно имеет вид
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,410
- гуманитарные 33,633
- юридические 17,906
- школьный раздел 608,042
- разное 16,856
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.