Уравнение взаимного ориентирования в базисной системе координат (2 видео)

Уравнение взаимного ориентирования

Одной из важнейших задач фотограмметрии является взаимное ориентирование снимков. Основание для ее решения было предложено С. Финстервальдером в 1899 г. как условие пересечения в пространстве пары соответственных лучей. Аналитическое решение задачи предложено профессором А.С. Скиридовым в 1928 г.

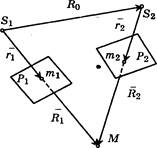
На рис. 9.9 изображена пара снимков Pi и Р2 и связки проектирующих лучей в том положении, которое они занимали в момент фотографирования. Любая пара соотвегственных лучей (например, Sinti и S2^2) пересекается и находятся в одной плоскости, проходящей через базис фотографирования S1S2. При изменении положения одной из связок проектирующих лучей соответственные лучи окажутся в разных плоскостях, в точке М не пересекутся, и модель разрушится.

Следовательно, условием взаимного ориентирования пары снимков является размещение соответственных векторов в одной базисной плоскости и их пересечение в одной точке. Математически это описывается условием компланарности векторов R₉ Д2 и До > т — е — условием равенства нулю их векторно-скалярного произведения, численно равного объему построенного на этих векторах параллелепипеда:

До х (Ri х Д₂) = 0 .

Уравнение взаимного ориентирования в базисной системе координат

Полученное условие связывает направления трех векторов, любой из которых можно разделить на свой модуль, поэтому можно записать

До x(ri хг₂) = 0. (9.10)

Выражение (9.10) инвариантно по отношению к системе координат, в которой

Рис. 9.9. Условие взаимного ори ентирования снимков

представлены векторы До, п, гг , и в самом общем случае его можно записать в матричном виде следующим образом:

J59

B X B Y B Z

x y; z x y’ z;

= o,

где, согласно рис. 9.4 и 9.8,

Запишем условие (9.11) для рассмотренных выше систем элементов взаимного ориентирования.

В базисной системе элементов взаимного ориентирования (рис. 9.7) ось абсцисс координатной системы SiX’Y’Z’ совпадает с базисом фотографирования, Вх = В, By = Bz = 0, и вместо (9.11) будем иметь:

в
№	Y <	Z[
*2	Y*	Z’2

о,

где в соответствии с (3.4)

1 = c i*i + c 2l/l — с 3/> ^2 = С 1 Х 2 + С 2У2 — ^’ J

Здесь В — базис фотографирования; X?T,Z’ и Х’г^’г^’г

координаты точек т и Ш2 в системах SjX’iY’iZ’i и йг-ХГ^Уг^’г; &’*» c’j, b»j, c»i (i = 1, 2, 3) — направляющие косинусы, определяемые по формулам (3.8) с заменой углов а, со, х элементами взаимного ориентирования ct’i, oo’i = 0, x’i для левого снимка и а’г, со’г, Х*2 ДЛ Я правого.

Раскроем определитель (9.13) и разделим обе его части на величину Б:

Умножив это уравнение на (-f/Z’iZ^), после несложных преобразований с учетом (3.21) получим еще одну форму записи уравнения взаимного ориентирования в базисной системе

У?

У°2=Я° = 0,

интерпретируемую как условие равенства нулю поперечных параллаксов точек трансформированных снимков, или условие равенства их трансформированных ординат. Последнее и объясняет отсутствие

Поперечных параллаксов при стереоскопическом наблюдении эпи-полярных изображений.

Приведем уравнение (9.15) к линейному виду, представив элементы взаимного ориентирования в явном виде. Для этого заменим в формулах (3.8) тригонометрические функции углов а, со и х их разложениями в ряды с удержанием членов первого порядка малости

b 2 = с з = !» bi =

а 2 = Ъ c i = _а з = а > с 2 =

& з = — = У и после простых преобразований получим уравнение взаимного ориентирования в линейном виде:

В линейно-угловой системе элементов взаимного ориентирования (рис. 9.8) принята система координат левого снимка Sxyz, составляющие базиса фотографирования определяются формулами (9.12), а фотограмметрические координаты точек левого снимка соответствуют измеренным. С учетом этого вместо (9.11) будем иметь, разделив первую строку на В_х: |1 tgx’ tgv’/cosi’l

= 0, (9.18)

Р^2 ^2 ^2

Где

Зак. 344

. рх’ + ^v’ + ^/Дсс + (/ + ^)Асо + х₂Ах — g = 0 . (9.19)

Уравнения (9.17) и (9.19) пригодны для определения элементов взаимного ориентирования только плановых снимков. Для этого измеряют координаты и параллаксы как минимум пяти точек, составляют для каждой из них уравнение (9.17) или (9.19) и решают полученную систему уравнений.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Фотограмметрия построение и уравнивание аналитической фототриангуляции (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6

Рис. 1.5. Первая система углов АФС Рис. 1.6. Вторая система углов АФС

Таким образом, аэроснимок имеет девять элементов ориентирования три элемента внутреннего ориентирования и шесть элементов внешнего ориентирования. Из шести элементов внешнего ориентирования три – линейные, три угловые. Из них и или и фиксируют направление главного луча, а — поворот вокруг главного луча.

Знание угловых элементов внешнего ориентирования снимка дает возможность сформировать матрицу ортогональных преобразований , позволяющую осуществить переход от вспомогательной системы координат к системе координат и, тем самым найти в этой системе вектор положения точки на снимке:

. (1.5)

Матрица ортогональных преобразований будет определяться системой углов Эйлера и для 1-ой и 2-ой систем углов ориентирования соответственно равна (см. Рис. 1.5, Рис. 1.6):

, (1.6)

. (1.7)

Компоненты матрицы определяться:

· для углов :

; (1.8)

· для углов :

. (1.9)

Основные формулы одиночного снимка.

В фотограмметрии уравнениями коллинеарности фактически называют два уравнения:

· уравнение связи между координатами соответственных точек местности и снимка;

· зависимость между координатами точки снимка и координатами соответствующей точки местности.

Векторы и коллинеарны:

, (1.10)

где — скаляр. Учитывая выражение (1.5) для будем иметь

. (1.11)

Переходя к координатной форме записи, исключая неизвестный скаляр получим соотношения:

. (1.12)

Полученные уравнения выражают условие коллинеарности векторов и являются основными формулами одиночного снимка. Формулы (1.12) выражают связь между координатами точки местности и координатами соответствующей точки снимка.

Легко получить формулы обратной связи используя равенство (1.11) и учитывая свойство ортогональной матрицы :

. (1.13)

Так же, осуществив переход к координатной форме записи и исключая неизвестный скаляр , получим соотношения:

. (1.14)

Здесь — есть элементы матрицы .

Полученные уравнения, так же, выражают условие коллинеарности векторов и устанавливают связь между координатами точки на снимке и координатами соответствующей точки местности. Выражение (1.14) в дальнейшем будем называть уравнением коллинеарности.

Уравнение коллинеарности (1.14) имеет важное значение в фотограмметрии и прежде всего в построении и уравнивании фототрангуляции способом связок, в построении макетных снимков, решении обратной фотограмметрической засечки, калибровки фотографических систем.

В уравнениях (1.12) и (1.14) в явном виде представлены элементы внутреннего ориентирования, линейные элемента внешнего ориентирования – координаты центра проекции. Угловые элементы внешнего ориентирования вошли в значения направляющих косинусов.

Все это означает следующее:

· в случае выражения (1.12) располагая точными значениями координат изображения точки, элементов внутреннего и внешнего ориентирования и цифровой моделью рельефа (ЦМР), мы можем получить только плановые координаты точки в пространстве предметов;

· в случае выражения (1.14) располагая цифровой моделью местности и элементами внешнего ориентирования, мы можем вычислить координаты изображения точки.

1.4. Обратная пространственная фотограмметрическая засечка

Сущность обратной пространственной фотограмметрической засечки состоит в определении элементов внешнего ориентирования снимка по опорным точкам.

Способы определения элементов внешнего ориентирования по опорным точкам можно разделить на две группы:

1. способы, позволяющие в результате решения уравнений непосредственно получить элементы внешнего ориентирования – прямые способы;

2. способы, в которых предполагается, что известны приближенные (предварительные) значения элементов внешнего ориентирования, а в результате решения находят поправки к этим значениям.

Способы второй группы допускают применение различных статистических методов, что имеет существенное значение, особенно для оценки надежности и точности определения элементов внешнего ориентирования. Способы первой группы можно рассматривать как источник предоставления предварительной информации об элементах внешнего ориентирования.

Способы второй группы основаны на использовании уравнения коллинеарности (1.14) и суть их состоит в следующем. Уравнения коллинеарности посредством линеаризации приводятся к линейному виду относительно определяемых параметров – элементов внешнего ориентирования, т. е. получают уравнения поправок. Далее формируется система уравнений, из решения которой, находятся поправки к предварительным значениям неизвестных. Решение выполняется методом последовательных приближений с последующей оценкой точности полученных элементов внешнего ориентирования. Для определения элементов внешнего ориентирования снимка необходимо иметь не менее трех опорных точек, поскольку, одна точка, измеренная на снимке, будет давать два уравнения. Число неизвестных, т. е. элементов ориентирования – шесть. Этот способ применим для любых значений элементов внешнего ориентирования.

Данный способ позволяет при определении элементов внешнего ориентирования учесть влияние элементов внутреннего ориентирования, величины которых в полете могут отличаться от значений, полученных в лабораторных условиях. При таком подходе для определения элементов ориентирования (внешнего и внутреннего) требуется не менее пяти опорных точек, поскольку, число неизвестных составляет девять. Следует отметить, что в случае равнинной местности система уравнений будет плохо обусловлена и точность определения элементов внутреннего ориентирования недостаточна. В этом случае.

Изложенный способ будет фактически подробно изложен в разделе (3.3), посвященном построению и уравнивание фототриангуляции аналитическим методом.

Обратная фотограмметрическая засечка применяется и для решения различных не топографических задач, например, для определения траектории, скорости и колебаний самолета, ракеты и других носителей.

1.5. Основные формулы пары снимков.

Прямая фотограмметрическая засечка.

Основные формулы пары снимков определяют зависимость между пространственными координатами точки местности и координатами ее изображений на паре снимков (стереопаре). Если элементы ориентирования снимков известны, то по этим формулам можно найти положение точек местности методом прямой фотограмметрической засечки.

Пусть с концов базиса получена пара снимков (Рис. 1.7). Величина и направление базиса фотографирования определяются вектором с началом в точке . В фотограмметрии, левый снимок стереопары принимают за основной.

Рис. 1.7 Связь между координатами точки местности и координатами ее

изображения на паре снимков углов АФС

Положение точки в пространстве можно определить вектором =в фотограмметрической системе координат , совмещенной с центром проекции левого снимка. Вектор =определяет положение той же точки в системе координат , совмещенной с центром проекции правого снимка.

Векторы и — векторы изображений точки в фотограмметрической системе координат, и, векторы изображений и той же точки во вспомогательной системе координат снимков, связаны соотношениями (1.5) :

, , где и — матрицы ортогональных преобразований, определяемые угловыми элементами ориентирования первого и второго снимков по формулам (1.8) или (1.9).

Векторы и , и коллинеарны: , .

С учетом геометрических условий векторов для пары снимков очевидно векторное произведение:

или . (1.15)

Переход к координатной форме позволяет получить соотношения для вычисления скаляра :

. (1.16)

Положение точки в пространстве определится:

. (1.17)

Таким образом, наличие второго снимка дает возможность найти неизвестный скаляр, который в случае одиночного снимка для решения поставленной задачи требовал его исключения (выражение (1.11)), что приводит к сокращению числа определяемых параметров до двух.

Решение прямой фотограмметрической засечки требует знания элементов внутреннего и внешнего ориентирования каждого снимка стереопары.

1.6. Элементы взаимного ориентирования

Принято различать две системы элементов взаимного ориентирования.

В первой системе неподвижным считают базис фотографирования, во второй левый снимок стереопары.

Первая система (базисная система, Рис (1.8.)). Элементами взаимного ориентирования в этой системе являются:

— угол в главной базисной плоскости левого снимка между главным лучом (оптической осью) левой связки и перпендикуляром к базису:

— угол на левом снимке между осью и следом плоскости ;

— угол в главной базисной плоскости левого снимка между перпендикуляром к базису и проекцией главного луча (оптической оси) правой связки ;

— угол между проекцией главного луча (оптической оси) правой связки на базисную плоскость левого снимка и главным лучом :

— угол на правом снимке между осью и следом плоскости .

Рис. 1.8. Первая система элементов взаимного ориентирования

Углы и называются продольными углами наклона снимков относительно базиса фотографирования, — взаимным поперечным углом наклона, а углы и — углами поворота.

Началом пространственных координат в первой системе служит центр проекции левого снимка, ось совмещена с базисом, а ось находится в главной базисной плоскости левого снимка. Система координат параллельна системе координат .

Вторая система ( система левого снимка, Рис (1.9.)). Элементами взаимного ориентирования в этой системе являются:

— угол на левом снимке между осью и следом главной базисной плоскости левого снимка;

— угол наклона базиса относительно левого снимка;

— взаимный продольный угол наклона снимков, составлен осью с проекцией главного луча (оптической оси) правой связки на плоскость ;

— взаимный поперечный угол наклона снимков, заключенный между плоскостью и главным лучом (оптической осью) правой связки;

— взаимный угол поворота снимков, угол на правом снимке между осью и следом плоскости ;

Рис. 1.9. Вторая система элементов взаимного ориентирования

Началом фотограмметрических координат служит центр проекции левого снимка, но координатные оси и направлены параллельно соответствующим осям и левого снимка. Ось совмещена с главным лучом (оптической осью) левой связки. Система координат параллельна системе координат .

Зная элементы взаимного ориентирования снимков можно найти координаты любой точки модели в фотограмметрической системе координат.

1.7. Условие компланарности векторов.

Уравнение взаимного ориентирования.

Условие компланарности векторов – критерий пересечения соответственных лучей. Пара соответственных лучей пересекается, если она лежит в одной базисной плоскости – плоскости, проходящей через базис съемки. В этом случае можно говорить, что снимки стереопары взаимно ориентированы. Критерий взаимного ориентирования можно представить в виде условия компланарности векторов. В общем случае данный критерий будет иметь вид (см. Рис. 1.7.):

, (1.18)

, (1.19)

где и — векторы, определяющие базис съемки , и — векторы, определяющие соответственные точки на левом и правом снимках.

Не любые изменения взаимного положения снимков нарушают пересечение соответственных лучей. Например, если правый или левый снимок взаимно ориентированной пары совершает только поступательное движение и при этом центр проекции его не смещается с линии базиса, то пересечение соответственных лучей сохраняется. Это следует и из условия (1.18). Любой из векторов, входящих в это выражение можно разделить на его модуль. Уравнение (1.18) связывает между собой только направления соответственных лучей и базиса. Длина базиса в этом случае не имеет значения и может быть произвольной.

Условие компланарности векторов имеет важное значение в фотограмметрии и находит применение в определении элементов взаимного ориентирования, в построении, и уравнивании фототрангуляции.

Уравнение взаимного ориентирования – уравнения, связывающие элементы взаимного ориентирования снимков с координатами соответствующих точек стереопары.

Условие компланарности векторов в общем случае в координатной форме будет иметь вид :

. (1.20)

Применительно к первой системе элементов взаимного ориентирования вектор , определяющий базис съемки, будет иметь компоненты: и условие компланарности векторов примет вид:

. (1.21)

Здесь векторы и — векторы изображений точки в фотограмметрической системе координат соответственно на левом и правом снимках, определяются выражением (1.5) : , , где и — векторы изображений той же точки, во вспомогательных системах координат снимков, определяются формулой (1.3), и — матрицы ортогональных преобразований, определяемые угловыми элементами взаимного ориентирования снимков по формулам (1.9).

При вычислении матрицы:

· — в формулы (1.9) вместо углов , , подставляются углы , , ;

· — в формулы (1.9) вместо углов , , подставляются углы , , .

Условие компланарности векторов в координатной форме применительно ко второй системе элементов взаимного ориентирования учитывая, что и , так как, матрица — единичная, будет иметь вид:

. (1.22)

Здесь первая строка разделена на , — вектор изображения точки в фотограмметрической системе координат определится по формуле (1.5) : . Вектор изображения той же точки во вспомогательной системе координат правого снимка, определится выражением (1.3). Матрица ортогональных преобразований вычислится по угловым элементам взаимного ориентирования по формулам (1.9). При вычислении матрицы в формулы (1.9) вместо углов , , подставляются углы , , .

Из равенств (1.21) и (1.22) следуют условия:

для первой системы элементов взаимного ориентирования

; (1.23)

для второй системы элементов взаимного ориентирования

. (1.24)

В эти условия входят все элементы взаимного ориентирования пары снимков. Именно данные выражения лежат в основе алгоритмов определения элементов взаимного ориентирования.

Рассмотрим принцип определения элементов взаимного ориентирования. В общем случае уравнения (1.23), (1.24) можно представить в таком виде:

для первой системы

; (1.25)

для второй системы

. (1.26)

Функции и являются нелинейными относительно определяемых параметров – элементов взаимного ориентирования. Поэтому, для их определения прибегают к стандартной процедуре: данные функции линеаризуют, т. е. приводят к линейному виду, посредством разложения в ряд Тейлора в окрестности точки, задаваемой вектором предварительных значений неизвестных:

— для первой системы элементов;

— для второй системы элементов.

В результате строится уравнение поправок:

, (1.27)

где , — матрица частых производных, вычисляемая по предварительным значениям определяемых параметров соответственно для первой и второй системы элементов взаимного ориентирования;

— вектор поправок к предварительным значениям определяемых параметров соответственно для первой и второй системы элементов взаимного ориентирования;

Видео:Семинар №4 "Замена базиса и системы координат"Скачать

Условие, уравнения и элементы взаимного ориентирования снимков

На рис. 1 представлена стереопара снимков Р₁ и Р₂ в положении, которое они занимали в момент фотографирования.

Любая пара соответственных лучей в этом случае пересекается в точке М местности и лежит в плоскости, проходящей через базис фотографирования (базисной плоскости).

Очевидно, что в этом случае векторы , лежащие в базисной плоскости, компланарны.

Рис. 1

Как известно из аналитической геометрии, смешанное произведение компланарных векторов равно нулю.

. ( .1)

Условие компланарности в координатной форме имеет вид:

. ( 2)

В уравнении ( 2) координаты векторов в системе координат фотограмметрической модели О_МХ_МY_MZ_M, в общем случае произвольно расположенной и ориентированной.

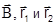
В дальнейшем эту систему координат будем называть просто системой координат модели.

Условие ( 2) связывает между собой только направления векторов и выполняется при любых значениях их модулей. Поэтому значение модуля вектора можно выбрать произвольно. Направление вектора определяется двумя независимыми величинами. В качестве этих величин можно выбрать координаты b_z и b_у вектора , коллинеарного вектору , задав величину координаты b_x произвольно.

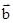
В частном случае величину b_x можно выбрать равной 1.

При этом направление вектора будут определять величины:

и .

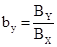
Выражение (2) в этом случае будет иметь вид:

( 3)

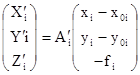
где i – номер снимка, а А’₁ – ортогональная матрица, элементы a_ij которой являются функциями угловых элементов ориентирования i-го снимка w_i’,a_i’,À_i’ относительно системы координат модели О_МХ_МY_MZ_M.

В выражении (3), которое является уравнением взаимного ориентирования в общем виде, куда кроме координат соответственных точек, измеренных на стереопаре снимков, и элементов внутреннего ориентирования входят 8 параметров b_y, b_z, w₁’, a₁’, À₁’, w₂’, a₂’, À₂’, которые определяют угловую ориентацию базиса фотографирования и стереопары снимков относительно системы координат модели О_МХ_МY_MZ_M.

Причем параметры w₁’ и w₂’ определяют поворот снимков стерепары вокруг оси Х_М, параметры b_z, a₁’, a₂‘ – поворот базиса фотографирования и стереопары снимков вокруг оси Y_M, а параметры b_y, À₁’, À₂ ‘ – поворот базиса фотографирования и стереопары снимков вокруг оси Z_M.

Однако, из этих 8 параметров только 5 определяют взаимную угловую ориентацию базиса фотографирования и стереопары снимков.

Условие (3) выполняется при любой ориентации системы координат модели О_МХ_МY_MZ_M. Следовательно, ее можно ориентировать таким образом, чтобы 3 из 8 параметров стали равны нулю.

Очевидно, что в общем случае можно сделать равным нулю только один из параметров, входящих в три группы параметров:

Таким образом, в качестве элементов взаимного ориентирования можно выбрать любую комбинацию из восьми параметров b_y, b_z, w₁’, a₁’, À₁’, w₂’, a₂’, À₂’, кроме комбинаций, в которые одновременно входят две тройки параметров b_z, a₁’, a₂‘ и b_y, À₁’, À₂’, а также пара параметров w₁’ и w₂’.

Рассмотрим наиболее распространенные системы элементов взаимного ориентирования:

. ( 4)

; ( 5)

так как .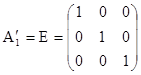

Комментарий. 3 оставшихся из 8 параметров после выбора 5 элементов взаимного ориентирования задают ориентацию системы координат модели О_МХ_МY_MZ_M. Например, выбрав систему элементов взаимного ориентирования b_y, b_z, w₂’, a₂’, À₂’ и приняв, что w₁’= a₁’= À₁’ =0, мы таким образом задаем систему координат модели О_МХ_МY_MZ_M, которой параллельны осям x, y, z системы координат первого снимка стереопары S₁x₁y₁z₁. В общем случае значения трех параметров можно задавать произвольно.

5. Определение элементов взаимного ориентирования

Для определения элементов взаимного ориентирования в качестве исходного используют уравнения взаимного ориентирования ( 4.3)

Каждая точка, измеренная на стереопаре снимков, позволяет составить одно уравнение (4.3), в которое, помимо измеренных координат точек на стереопаре снимков, элементов внутреннего ориентирования и трех параметров, задающих ориентацию системы координат модели, входят 5 неизвестных элементов взаимного ориентирования.

Очевидно, что для определения элементов взаимного ориентирования необходимо измерить на стереопаре снимков не менее 5 точек.

В качестве примера рассмотрим определение элементов взаимного ориентирования b_y, b_z, w₂’, a₂’, À₂’.

В связи с тем, что уравнения ( 4.3) не линейны, их предварительно приводят к линейному виду и переходят к уравнению поправок:

. ( 1)

В уравнении поправок коэффициенты a_i частные производные от функции ( 4.3) по соответствующим аргументам, а ℓ– свободный член.

Значения коэффициентов а_i в уравнении ( 1) вычисляют по следующим известным значениям:

– измеренным координатам точек на стереопаре снимков – х_i, y_i;

– 3 параметрам, задающим ориентацию системы координат модели (в нашем случае w₁’, a₁’, À₁’) и приближенным значениям элементов взаимного ориентирования.

Свободный член ℓ вычисляется по формуле ( 4.3) таким же образом.

Полученную систему уравнений поправок решают методом приближений, а в случае, если измерено более 5 точек по методу наименьших квадратов (под условием V T PV=min). В результате решения находят значения элементов взаимного ориентирования.

Критерием, по которому принимается решение о завершении итерраций, могут являться величины поправок к определяемым неизвестным или величины остаточных поперечных параллаксов, которые для каждой измеренной точки вычисляются по формулам:

; ( 2)

где .

Величина q_ост представляет собой разность ординат измеренных точек на стереопаре снимков, приведенных к идеальному случаю съемки, то есть q=y₁-y₂.

Необходимо отметить, что при отсутствии ошибок построения снимка и ошибок измерений величина q должна быть равна 0.

При определении элементов взаимного ориентирования оптимальным вариантом считается измерение 12-18 точек на стереопаре снимков, расположенных парами или тройками в 6 стандартных зонах (рис. 1).

Рис. 1

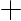— главная точка снимка

— стандартно расположенная зона

В этом случае получается наиболее точное и надежное определение элементов взаимного ориентирования и появляется возможность локализации грубых измерений.