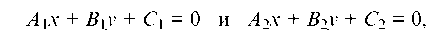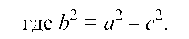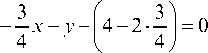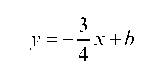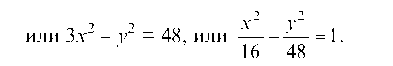Уравнение высоты в аналитической геометрии (3 видео)

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

Найти уравнение стороны треугольника.
Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Содержание

Примеры решений по аналитической геометрии на плоскости
Решения задач о треугольнике онлайн
1.3. Аналитическая геометрия. Аналитическая геометрия на плоскости
🔍 Видео

Видео:Уравнения стороны треугольника и медианыСкачать

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Видео:Аналитическая геометрия на плоскости. Решение задачСкачать

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

1.3. Аналитическая геометрия. Аналитическая геометрия на плоскости

1.3.1. Аналитическая геометрия на плоскости

Если на плоскости произвольно взята декартова система координат, то всякое уравнение первой степени относительно текущих координат х и у

где А и B одновременно не равны нулю, определяет прямую в этой системе координат.

Верно и обратное утверждение: в декартовой системе координат всякая прямая может быть представлена уравнением первой степени вида (1.24).

Уравнение (1.24) называется общим уравнением прямой.

Углом наклона прямой к оси Ох называется наименьший угол j, на который нужно повернуть в положительном направлении ось абсцисс до ее совпадения с данной прямой. Направление любой прямой характеризуется ее угловым коэффициентом к, который определяется как тангенс угла наклона j этой прямой к оси Ох, т. е.

Исключение составляет только лишь прямая, перпендикулярная оси Ох, которая не имеет углового коэффициента.

Уравнение прямой, имеющей угловой коэффициент к и пересекающей ось Оу в точке, ордината которой равна b (начальная ордината), записывается в виде:

Частные случаи уравнения (1.24) приведены в следующей таблице.

Угловой коэффициент к прямой, заданной общим уравнением Ax + By + C= 0, находится как коэффициент при х в выражении у через х:

Угловой коэффициент к прямой, заданной двумя точками вычисляется по формуле

Уравнением прямой в отрезках называется уравнение вида:

где а и b — соответственно абсцисса и ордината точек пересечения прямой с осями Ох и Oy, т. е. длины отрезков, отсекаемых прямой на координатных осях, взятые с определенными знаками.

Уравнение прямой, проходящей через точкуИ имею

щей угловой коэффициент к, записывается в виде:

Пучком прямых называется совокупность прямых плоскости, проходящих через одну и ту же точку А — центр пучка. Уравнение (1.28) можно рассматривать как уравнение пучка прямых, поскольку любая прямая пучка может быть получены из уравнения (1) при соответствующем значении углового коэффициента к. Исключение составляет лишь одна прямая пучка, которая параллельна оси Oy — ее уравнение х = xA.

Уравнение прямой, проходящей через две данные точки имеет вид:

Если точки A и B определяют прямую, параллельную оси Или оси, то уравнение такой прямой за

писывается соответственно в виде:

Условия пересечения, параллельности или совпадения двух прямых, заданными своими общими уравнениями

приведены в следующей таблице.

Если известны угловые коэффициенты прямых, то ус

ловие параллельности этих прямых состоит в равенстве их угловых коэффициентов:

Условие перпендикулярности двух прямых, угловые коэффициенты которых соответственно равныСостоит в выполнении соотношения

т. е. угловые коэффициенты этих прямых обратны по абсолютной величине и противоположны по знаку.

Под углом между двумя прямыми понимается один из двух смежных углов, образованных при их пересечении. Тангенс угла j между двумя прямыми, угловые коэффициенты которых соответственно равны к1 и к2, вычисляется по формуле

причем знак «плюс» соответствует острому углу, а знак «минус» — тупому.

Уравнение окружности с центром в точке S^; b) и радиусом r имеем вид:

Это каноническое уравнение окружности (рис. 7).

Уравнение второй степени относительно текущих координат х и у является уравнением окружности тогда и только тогда, когда в этом уравнении коэффициенты при квадратах координат равны, а член с произведением координат отсутствует. Таким образом, это уравнение имеет вид:

В этом случае говорят, что окружность задана общим уравнением.

Для определения координат центра и радиуса окружности, заданной общим уравнением, надо с помощью тождественных преобразований уравнение (1.35) привести к виду (1.34).

Эллипс есть геометрическое место точек, сумма расстояний которых от двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная (2а), большая, чем расстояние между фокусами (2с).

Простейшее уравнение эллипса получается, если расположить координатную систему следующим образом: за ось Оx принять прямую, проходящую через фокусы F1 и F2, а за ось Оу — перпен-

дикуляр к оси абсцисс в середине отрезка F1F2 (рис. 8). Тогда уравнение эллипса примет вид:

Точки А1 и А2, B1 и B2 пересечения эллипса с его осями симметрии (координатными осями) называются вершинами эллипса. Отрезки А1А2 = 2а и B1B2 = 2b называются осями эллипса, причем А1А2 — большой осью, а B1B2 — малой осью, так как а > b. Таким образом, параметры а и b, входящие в уравнение эллипса, равны его полуосям.

Эксцентриситетом эллипса называется отношение расстояния между фокусами к его большой оси, т. е.

Очевидно, что е а и уже большой осью будет отрезок B1B2 = 2b, а малой осью — отрезок А1А2 = 2а. Эксцентриситет такого эллипса вычисляется по формуле

Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная (2а), меньшая, чем расстояние между фокусами (2с).

Простейшее уравнение гиперболы получается, если расположить координатную систему следующим образом: за ось Ох принять прямую, проходящую через фокусыА за ось Оу — перпендикуляр в середине отрезка(рис. 10). Тогда уравнение гиперболы примет вид:

Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках А1 и А2, называемых вершинами гиперболы. Отрезок.Называется действительной осью гиперболы, а отрезок— мнимой осью гиперболы.

Таким образом, параметры а и b, входящие в уравнение гиперболы, равны ее полуосям.

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к ее действительной оси:

Ее асимптоты те же, что и у гиперболы (1.39).

Гиперболы (1.39) и (1.42) называются сопряженными. Гипербола называется равносторонней, если ее действительные и мнимые оси равны, т. е. а = b. Простейшее уравнение равносторонней гиперболы имеет вид:

Если мнимая ось гиперболы направлена по оси Ох и имеет длину 2а, а действительная ось длиной 2b направлена по оси Oy, то уравнение гиперболы (рис. 11) имеет вид:

Эксцентриситет такой гиперболы вычисляется по формуле

Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой параболы.

Величина р, равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно ее директрисе, называется осью, а точка пересечения параболы с ее осью — вершиной параболы.

Простейшее уравнение параболы получается, если координатная система расположена следующим образом: за одну из координатных осей берется ось параболы, а за другую — прямая, перпендикулярная оси параболы и проведенная посредине между фокусом и директрисой.

Тогда уравнение параболы примет вид:

определяет параболу, ось которой перпендикулярна оси абсцисс.

определяет параболу, ось которой перпендикулярна оси ординат.

Уравнения (1.48) и (1.49) приводятся к простейшему виду (1.44 — 1.47) путем тождественных преобразований с последующим параллельным переносом координатной системы.

Пример 1.16. Даны вершины А (2; 1), В (6; 3), C (4; 5) треугольника. Найти: 1) длину стороны АВ; 2) внутренний угол А в радианах с точностью до 0,01; 3) уравнение высоты, проведенной через вершину С; 4) уравнение медианы, проведенной через вершину С;

5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж.

Делаем чертеж (рис. 16).

1. Длину стороны АВ находим как расстояние между двумя точками А и В.

2. Для определения внутреннего угла А найдем уравнение прямой AC:

отсюда 2х — у — 3 = 0 или у = 2х — 3 и угловой коэффициент прямой AC равен: kAC = 2; далее находим уравнение прямой АВ:

Находим угол А отсюда

3. Уравнение высоты, проведенной через вершину C, ищем в виде у — yC = kCD (x — xC) и так как CD А прямой АВ, то

4. Для определения уравнения медианы CM находим координаты точки M, которая делит прямую АВ пополам

Уравнение прямой CM ищем в виде:

а это означает, что уравнение медианы имеет вид х = 4, т. е. прямая CM L Ох.

5. Точку пересечения высот треугольника найдем как точку К пересечения высот CD и BK.

Находим уравнение высоты ВК:

Решаем систему уравнений, описывающих прямые CD и BK:

Тогдат. е. координаты точ

ки К будут:

6. Для нахождения длины высоты CD запишем нормальное уравнение прямой АВ:

7. Находим систему линейных неравенств, определяющих внутреннюю область треугольника.

Найдем уравнение прямой BC:

Итак:

Берем любую точку, лежащую внутри треугольника, например, (4; 3) и подставляем ее координаты в левую часть уравнений прямых:

следовательно, система неравенств имеет вид:

Пример 1.17. Составить уравнение прямой I, проходящей через точку А (2; -4) и отстоящей от начала координат на расстоянии, равном 2 единицам.

Решение. Пусть уравнение искомой прямой имеет вид:

Для определения углового коэффициента к этой прямой воспользуемся тем, что она отстоит от начала координат на расстоянии, равном 2 единицам. Найдем это расстояние непосредственно. Уравнение перпендикуляра, опущенного из начала координат на прямую, имеет вид илиРешив совместно уравнения этих двух прямых

С другой стороны, по условию OC = 2. Таким образом, получаем уравнение для нахождения углового коэффициента к искомой прямой I:

получим координаты точки C их пересечения:

Отсюда находим расстояние от начала координат до прямой I:

В заключение отметим, что отыскивая уравнение прямой I в виде у — yA = k(x — Xa), мы предполагали тем самым, что эта прямая не параллельна оси ординат. Но очевидно, что прямая х = 2 (параллельная оси Оу) также удовлетворяет условию задачи, так как она проходит через точку А (2; -4) и отстоит от начала координат на расстоянии, равном 2 единицам (рис. 17).

Пример 1.18. Составить уравнения прямых, параллельных прямой 3х + 4у — 1 = 0 (I) и отстоящих от нее на расстоянии равном 1.

Решение. Уравнение каждой из прямых будем искать в виде Так как искомая прямая параллельна прямой I, то ее

угловой коэффициентИ, следовательно, ее уравнение при

нимает вид:

Для отыскания параметра b воспользуемся тем, что расстояние от любой точки прямой I, например, от точки А (3; -2) до прямой (*) согласно условию равно 1. Но это расстояние может быть вычислено и непосредственно. Запишем для этого

уравнение прямой h, проведенной из точки А перпендикулярно прямой I: