1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Уравнение высоты тетраэдра по координатам вершинУчасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів! Контакты
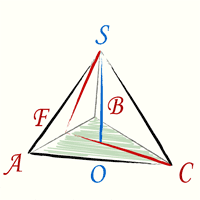
Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра (h — высота тетраэдра, a — ребро тетраэдра) Видео:Уравнения стороны треугольника и медианыСкачать  Вывод формулы высоты тетраэдраЧтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS: Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1). Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC . Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней. Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Правильный тетраэдр – частный вид тетраэдраТетраэдр, у которого все грани равносторонние треугольник называется правильным.
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать  Вычисление объема тетраэдра, если известны координаты его вершинПусть нам даны координаты вершин тетраэдра Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать  СвойстваЗная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2 Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2 Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2) Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8 В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4 🎥 ВидеоЗадача 6. Вычислить объём тетраэдра с вершинами в точках и его высоту, опущенную из вершины на граньСкачать  Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать  Задача C2: координаты вершин тетраэдраСкачать  Нахождение высоты тетраэдра.Скачать  Уравнение прямой и треугольник. Задача про высотуСкачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Вычисляем угол через координаты вершинСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Математика без Ху!ни. Уравнение плоскости.Скачать  Уравнение высоты пирамиды (устар.)Скачать  найти уравнение высоты треугольникаСкачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  | |||
Треугольники, из которых состоит тетраэдр, называются его гранями. 
Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.
, где 
, 
, 
проведем векторы 
, 
, 
. 
