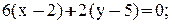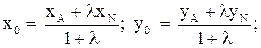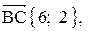Видео:Уравнения стороны треугольника и медианыСкачать
We are checking your browser. mathvox.ru
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Вычисляем высоту через координаты вершин 1Скачать
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 702944c89ba19d37 • Your IP : 87.119.247.227 • Performance & security by Cloudflare
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
Уравнение высоты треугольника
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать
Уравнение высоты треугольника по координатам формула
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Даны координаты вершин треугольника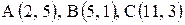 
.
1) Вычислить длину стороны 
.
2) Составить уравнение линии .
3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.
4) Найти точку пересечения медиан.
5) Найти косинус внутреннего угла при вершине В.
6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.
А
1. Длина стороны ВС равна модулю вектора 
.
; 
.
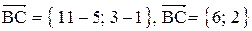
2. Уравнение прямой ВС: 
; 
; 
.
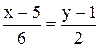
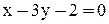
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку 
перпендикулярно вектору 
: 
. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: 
.
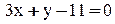
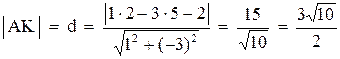
4. Найдем координаты точки N – середины стороны ВС:
; 
; 
.
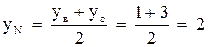
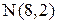
Точка пересечения медиан О делит каждую медиану на отрезки в отношении 
.
Используем формулы деления отрезка в данном отношении 
:
.
5. Косинус угла при вершине В найдем как косинус угла между векторами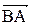 
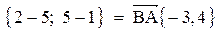
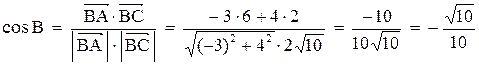
и 
; 
.
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы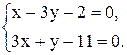 
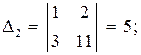
Систему решим по формулам Крамера: 
.
Точка К является серединой отрезка АМ.
.
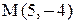
Контрольные варианты к задаче 2
Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение линии ВС;
3) составить уравнение высоты, проведенной из вершины А;
4) вычислить длину высоты, проведенной из вершины А;
5) найти точку пересечения медиан;
6) вычислить внутренний угол при вершине В;
7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.
| 1. | 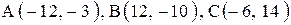 . | 2. |  . |
| 3. |  . | 4. |  . |
| 5. |  . | 6. |  . |
| 7. |  . | 8. |  . |
| 9. | 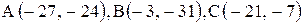 . | 10. |  . |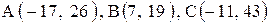
| 11. | 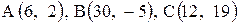 . | 12. |  . |
| 13. |  . | 14. |  . |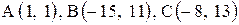
| 15. | 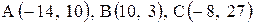 . | 16. |  . |
| 17. | 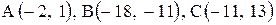 . | 18. |  . |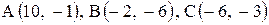
| 19. | 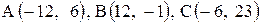 . | 20. |  . |
| 21. | 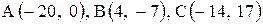 . | 22. |  . |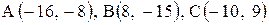
| 23. | 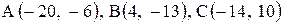 . | 24. |  . |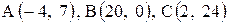
| 25. |  . | 26. |  . |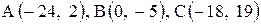
| 27. | 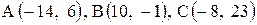 . | 28. |  . |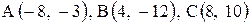
| 29. | 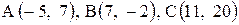 . | 30. |  . |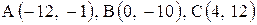
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10637 – 
| 8008 – 
или читать все.
| ЛУЧШИЙ ОТВЕТ |
Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @
Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)
Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:
Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0
Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9
Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:
y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.
10 = (32/3) + d,
d = -2/3
Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0
Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: XE = 6, YE = -1
Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.
(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0
Это уравнение медианы AE.
Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:
S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)
📹 Видео
Задача 6. Вычислить объём тетраэдра с вершинами в точках и его высоту, опущенную из вершины на граньСкачать
найти уравнение высоты треугольникаСкачать
Уравнение прямой и треугольник. Задача про высотуСкачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
Разбор Задачи №16 из Варианта Ларина №285Скачать
Вычисляем угол через координаты вершинСкачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Даны координаты вершин треугольника АВС.Скачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
Аналитическая геометрия на плоскости. Решение задачСкачать
№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать
Уравнения прямой на плоскости | Векторная алгебраСкачать
Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать
