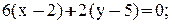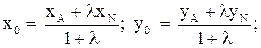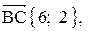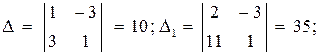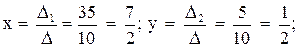Уравнение высоты и ее схема

Видео:Уравнения стороны треугольника и медианыСкачать

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Видео:найти уравнение высоты треугольникаСкачать

Высота треугольника онлайн

С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Видео:Уравнение прямой и треугольник. Задача про высотуСкачать

Высота треугольника. Определение

Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

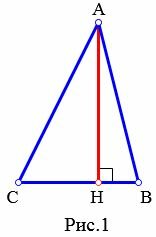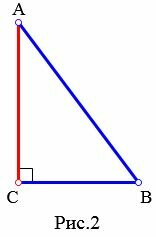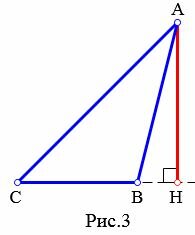Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).

Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Теорема о пересечении высот треугольника

Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.

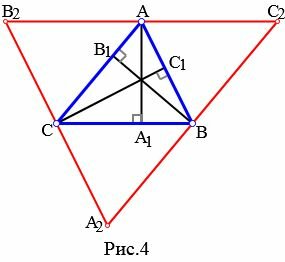Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.

Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.

Точка пересечения высот треугольника называется ортоцентром.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Высота треугольника по основанию и площади

Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).

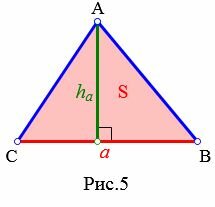Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:

.

.

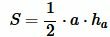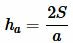(1)

Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.

Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:

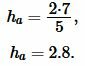Ответ:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Высота треугольника по трем сторонам

Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):

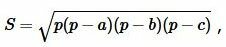(2)

где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:

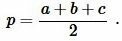(3)

Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:

.

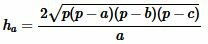(4)

Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):

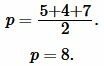Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:

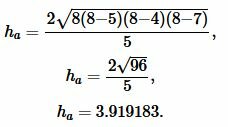Ответ:

Видео:Аналитическая геометрия на плоскости. Решение задачСкачать

Высота треугольника по двум сторонам и радиусу описанной окружности

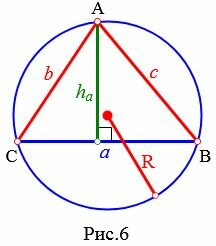Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:

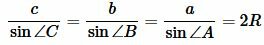(5)

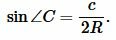(6)

Далее, из теоремы синусов имеем:

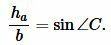(7)

Подставляя (6) в (7), получим:

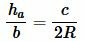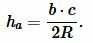(8)

Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:

Решение: Проверим сначала условие (9):

Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать

Высота треугольника по стороне и прилежащему к ней углу

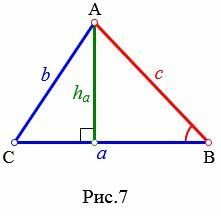Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:

Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Уравнение высоты треугольника по координатам формула

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Даны координаты вершин треугольника .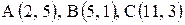

1) Вычислить длину стороны .

2) Составить уравнение линии .

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

А

1. Длина стороны ВС равна модулю вектора .

; .

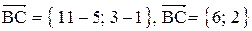
2. Уравнение прямой ВС: ; ; .

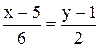
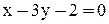
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку перпендикулярно вектору :

. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

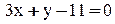
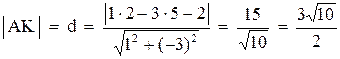
4. Найдем координаты точки N – середины стороны ВС:

; ; .

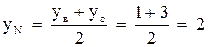
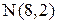
Точка пересечения медиан О делит каждую медиану на отрезки в отношении .

Используем формулы деления отрезка в данном отношении :

.

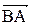
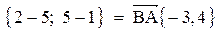
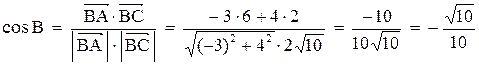
5. Косинус угла при вершине В найдем как косинус угла между векторами и ;

.

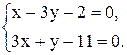
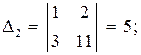
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы Систему решим по формулам Крамера:

.

Точка К является серединой отрезка АМ.

.

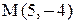
Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	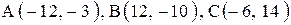.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	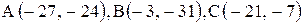.	10.	.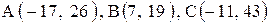
11.	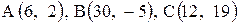.	12.	.
13.	.	14.	.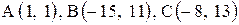
15.	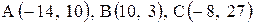.	16.	.
17.	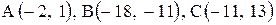.	18.	.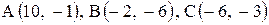
19.	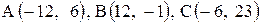.	20.	.
21.	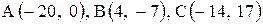.	22.	.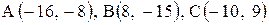
23.	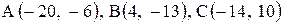.	24.	.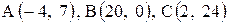
25.	.	26.	.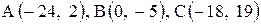
27.	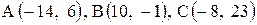.	28.	.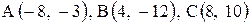
29.	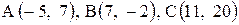.	30.	.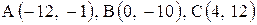

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10637 – | 8008 – или читать все.

Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @

Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)

Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:

Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0

Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9

Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:

y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.

10 = (32/3) + d,
d = -2/3

Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0

Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: X_E = 6, Y_E = -1

Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.

(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0

Это уравнение медианы AE.

Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:

S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)

🎦 Видео

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Математика это не ИсламСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепьюСкачать

Прямо пропорциональная и обратно пропорциональная зависимость. 6 класс.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать