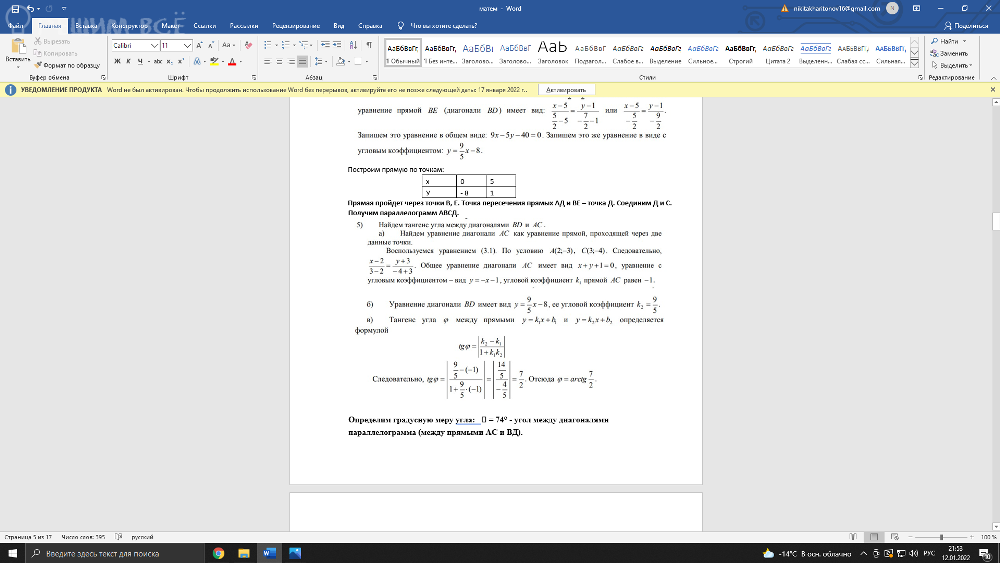
Уравнение высоты bk опущенной из вершины в на сторону ad (2 видео)

Задача 62577 здравствуйте, уважаемые эксперты! Прошу.

Содержание

Условие
Решение
Уравнение высоты bk опущенной из вершины в на сторону ad
ТЕМА 2. Векторная алгебра.
📽️ Видео

Условие

здравствуйте, уважаемые эксперты! Прошу Вас ответить на следующий вопрос:
Даны три последовательные вершины параллелограмма A(3;-2), B(1;-1), C(0;5)
Не находя координаты вершины D Найти:
1) Уравнение стороны AD
2) Уравнение Высоты BK, опущенной из вершины В на сторону AD
3) длину высоты BK
4) Уравнение диагонали BD
5) тангенс угла между диагоналями параллелограмма.
Записать общее уравнения найденных прямых. Построить чертеж.

НА ФОТО ПРИМЕР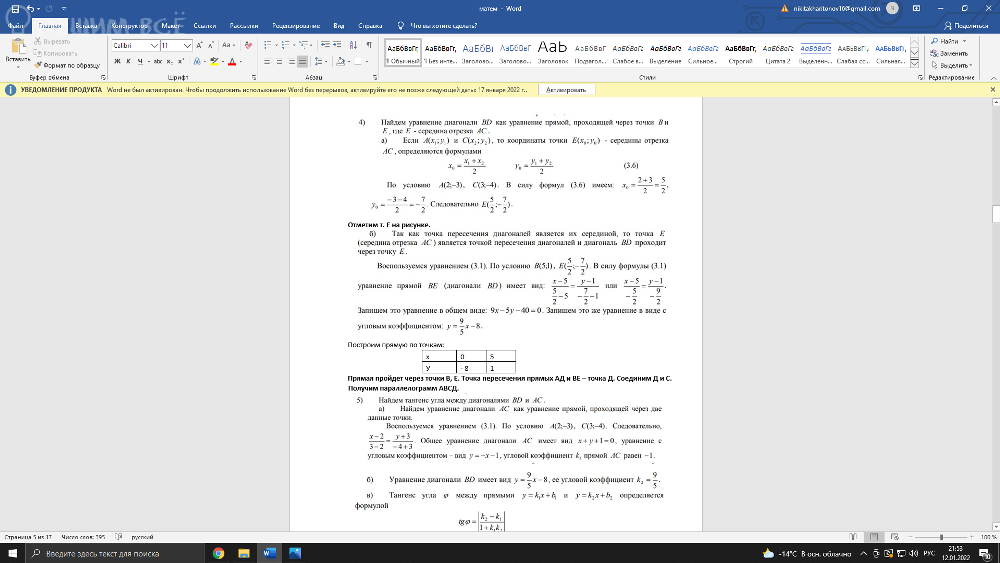

Решение

1) Уравнение стороны AD
Составляем уравнение стороны BC как прямой, проходящей ерез две точки:

[m]frac=frac[/m]- уравнение прямой с направляющим вектором (-1;6)

Параллельные прямые имеют одинаковые направляющие векторы

Составим уравнение прямой AD как прямой, проходящей через точку А с направляющим вектором

[m]y=-6x+16 [/m] — уравнение прямой AD c угловым коэффициентом k_(AD)=-6

2) Уравнение Высоты BK, опущенной из вершины В на сторону AD

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1):

y=(1/6)x+b — уравнение прямых, перпендикулярных AD

Подставим координаты точки B и найдем уравнение высоты BK

y=(1/6)x-(7/6) -[b] уравнение высоты ВК[/b]

4) Е — середина АС
A(3;–2), C(0;5)
E(3/2; 3/2)

Составляем уравнение прямой BE как прямой, проходящей через две точки:

3) длина высоты BK — расстояние от точки В до прямой AD находим по формуле:

Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать

Уравнение высоты bk опущенной из вершины в на сторону ad

Ответ:

Подразумевая, что задача для 7-ого/8-ого класса попробую решить ее наиболее понятным для Вас и подробным способом:

1) По определению параллелограмма сторона AD будет параллельна стороне BC. Мы знаем, что параллельные прямые имеют одинаковый коэффициент k (то есть у них одинаковый тангенс угла наклона).

Воспользуемся этим и зададим уравнение прямой BC.

Это проще всего сделать по формуле:

Однако Вам может быть этот способ непривычен.

Тогда составляете систему из двух уравнений, как Вас учили и приходите к тому же самому выводу.

Обратимся теперь к уравнению . Наша прямая проходит через точку A(3; -2). Тогда . Коэффициент мы нашли.

Подставим эти данные в уравнение и получим . Тогда искомое уравнение .

2) Прямая BK по определению высоты перпендикулярна стороне AD. Мы знаем, что в этом случае выполняется свойство . Тогда . Прямая проходит через точку B(1; -1). Тогда коэффициент будет равен , а все уравнение имеет вид .

3) Длина высоты BK может быть получена, например путем решения системы из уравнений, записанных в пунктах 1 и 2. Но ответ будет кривой. Подобную операцию вы всегда сможете сделать сами, а я позволю себе отойти немного в сторону.

Тогда . Так считать намного проще.

4) Точку D здесь использовать не запрещается. D(2, 4). Откуда уравнение будет .

Видео:Вычисляем высоту через координаты вершин 1Скачать

ТЕМА 2. Векторная алгебра.

Задача 1. Даны три последовательные вершины параллелограмма А(3;-4), В(-1;-1),С(4;2). Не находя координаты вершины D, найти:

1) уравнение стороны AD;

2) уравнение высоты BK, опущенной из вершины В на сторону AD;

3) длину высоты BK;

4) уравнение диагонали BD;

5) тангенс угла между диагоналями параллелограмма.

Записать общие уравнения найденных прямых. Построить чертеж.

Задача 2. Даны точки A(5;-3;2), B(3;2;-1), C(4;-2;1), D(3;1;0). Найти:

1) общее уравнение плоскости АВС;

2) общее уравнение плоскости, проходящей через точку D параллельно плоскости АВС;

3) косинус угла между плоскостью 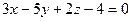и плоскостью ABC;

4) канонические уравнения прямой АВ;

5) канонические уравнения прямой, проходящей через точку D параллельно прямой AB;

6) канонические уравнения прямой, проходящей через точку D перпендикулярно плоскости ABC.

Задача 3. Уравнение кривой второго порядка 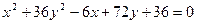путем выделения полного квадрата привести к каноническому виду. Построить кривую.

Задача 4. Кривая задана в полярной системе координат уравнением .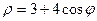

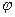
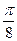
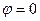
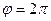
1) найти точки, лежащие на кривой, давая значения через промежуток, равный , начиная от до ;

2) построить полученные точки;

3) построить кривую, соединив построенные точки (от руки или с помощью лекала);

4) составить уравнение этой кривой в прямоугольной декартовой системе координат.

Задача 5. Построить на плоскости геометрическое место точек, определяемое неравенствами

1) ;

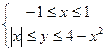
2) .

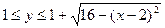
ТЕМА 2. Векторная алгебра.

1. Линейные действия над векторами (сложение, вычитание, умножение на число).

2. Нелинейные действия с векторами (скалярное произведение, векторное произведение, смешанное произведение).

3. Решение задач с помощью векторной алгебры. Условие коллинеарности, условие перпендикулярности, условие компланарности векторов.

Решение типового варианта контрольной работы.

Задание 1: Коллинеарны ли векторы и , разложенные по векторам и , где

Решение:

1. Вычислим проекции векторов на оси координат:

2. Два вектора коллинеарны, если их проекции на оси координат пропорциональны, следовательно, проверим пропорциональность проекций векторов на оси координат:

не коллинеарны.

Задание 2: Перпендикулярны ли векторы ?

Решение:Два вектора перпендикулярны , если их скалярное произведение равно 0,скалярное произведение векторов, заданных проекциями на оси координат, вычисляется по формуле: , где вычислим скалярное произведение:

векторы не перпендикулярны.

Задание 3: Компланарны ли векторы ?

Решение: Три вектора компланарны, если смешанное произведение векторов равно 0, смешанное произведение векторов вычисляется по формуле: , где вычислим смешанное произведение векторов:

векторы не компланарны.

Задание 4: При каком значении векторы где , перпендикулярны?

Решение:

1) Для определения , при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2) мы сможем найти из условия: , для этого найдем проекции векторов и на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора

Итак: векторы и перпендикулярны при и при

Задание 5: Даны точки:

Найти:

1. пр ;

2. ;

3. ;

4. орт вектора ;

5. ;

6. ;

Решение:

1. Из определения скалярного произведения следует, что проекцию вектора на вектор можно вычислить по формуле: пр где скалярное произведение векторов вычисляется по формуле: где и длина вектора: итак ,в нашем случае, формула принимает вид: для нахождения необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:

на основании формулы, выше написанной, получим :

пр ;

2. Для нахождения длины вектора воспользуемся формулой: , для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:

;

Итак:

3. Угол между векторами можно найти из определения скалярного произведения: в нашем случае формула принимает вид: находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:

Итак

4. Направление вектора определяется углами , образованными им с осями координат Косинусы этих углов (направляющие косинусы вектора) определяются по формулам: Направляющие косинусы вектора связаны соотношением мы имеем вектор единичной длины, такой вектор называется ортом для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину орт вектора .

Итак: орт вектора

5. Скалярное произведение векторов вычисляем по формуле:

(см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :

Итак:

6. Векторное произведение векторов вычисляется по формуле:

, где

Находим проекции векторов на оси координат:

Итак:

7. Смешанное произведение векторов вычисляется по формуле:

, где Итак:

Задание 6:Даны координаты вершин пирамиды:

Вычислить:

1. объем пирамиды;

2. длину ребра ;

3. площадь грани ;

Решение:

1. Объем пирамиды равен объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения объем

параллелипипеда, построенного на векторах как на ребрах равен:

Найдем проекции соответствующих векторов на оси координат:

Тогда объем пирамиды равен:

Вычислим объем по указанной формуле:

;

; (смотри пункт 5,3)

3. Площадь грани вычисляется по формуле:

так как грань треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения найдем проекции векторов на оси координат: