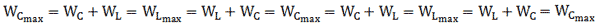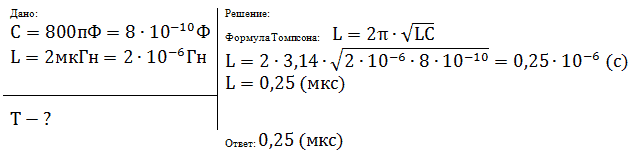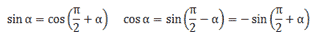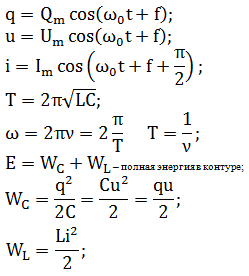Уравнение выражает зависимость силы тока от времени

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.

Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид

где q» — вторая производная заряда по времени. Величина

является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре дается формулой (Томсона):

Величина φ = ώt + φ , стоящая под знаком синуса или косинуса, является фазой колебания.

Фаза определяет состояние колеблющейся системы в любой момент времени t.

Ток в цепи равен производной заряда по времени, его можно выразить

Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,

где- угол между нормалью к рамке и вектором магнитной индукции .

По закону электромагнитной индукции Фарадея ЭДС индукции равна

где — скорость изменения потока магнитной индукции.

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции

где — амплитудное значение ЭДС индукции.

2. Если к контуру подключить источник внешней гармонической ЭДС

то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.

При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.

В промышленных цепях переменного тока России принята частота 50 Гц.

Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:

Поэтому количество теплоты, выделится за время Т:

Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:

Отсюда действующее значение тока

Аналогично действующее значение напряжения

Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.

Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.

называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего

Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.

Из уравнения следует, что . Период определим по формуле циклической частоты

Зависимость силы тока от времени имеет вид:

Амплитуда силы тока.

Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 510 3 А, ток изменяется по закону:

i=-5000 sin100t

Основным устройством, определяющим рабочую частоту любого генератора переменного тока, является колебательный контур. Колебательный контур (рис.1) состоит из катушки индуктивности L (рассмотрим идеальный случай, когда катушка не обладает омическим сопротивлением) и конденсатора C и называется замкнутым. Характеристикой катушки является индуктивность, она обозначается L и измеряется в Генри (Гн), конденсатор характеризуют емкостью C, которую измеряют в фарадах (Ф).

Пусть в начальный момент времени конденсатор заряжен так (рис.1), что на одной из его обкладок имеется заряд +Q , а на другой – заряд —Q . При этом между пластинами конденсатора образуется электрическое поле, обладающее энергией

, (1)

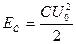
где 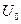– амплитудное (максимальное) напряжение или разность потенциалов на обкладках конденсатора.

После замыкания контура конденсатор начинает разряжаться и по цепи пойдет электрический ток (рис.2), величина которого увеличивается от нуля до максимального значения . Так как в цепи протекает переменный по величине ток, то в катушке индуцируется ЭДС самоиндукции, которая препятствует разрядке конденсатора. Поэтому процесс разрядки конденсатора происходит не мгновенно, а постепенно. В каждый момент времени разность потенциалов на обкладках конденсатора

(2)

(где – заряд конденсатора в данный момент времени) равна разности потенциалов на катушке, т.е. равна ЭДС самоиндукции

. (3)

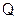
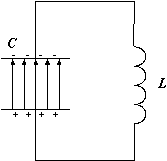Рис.1	Рис.2

Когда конденсатор полностью разрядится и , сила тока в катушке достигнет максимального значения (рис.3). Индукция магнитного поля катушки в этот момент также максимальна, а энергия магнитного поля будет равна

. (4)

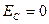
Затем сила тока начинает уменьшаться, а заряд будет накапливаться на пластинах конденсатора (рис.4). Когда сила тока уменьшится до нуля, заряд конденсатора достигнет максимального значения Q , но обкладка, прежде заряженная положительно, теперь будет заряжена отрицательно (рис. 5). Затем конденсатор вновь начинает разряжаться, причем ток в цепи потечет в противоположном направлении.

Так процесс перетекания заряда с одной обкладки конденсатора на другую через катушку индуктивности повторяется снова и снова. Говорят, что в контуре происходят электромагнитные колебания. Этот процесс связан не только с колебаниями величины заряда и напряжения на конденсаторе, силы тока в катушке, но и перекачкой энергии из электрического поля в магнитное и обратно.

Рис.3	Рис.4

Перезарядка конденсатора до максимального напряжения 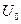произойдет только в том случае, когда в колебательном контуре нет потерь энергии. Такой контур называется идеальным.

В реальных контурах имеют место следующие потери энергии:

1) тепловые потери, т.к. R ¹ 0;

2) потери в диэлектрике конденсатора;

3) гистерезисные потери в сердечнике катушке;

4) потери на излучение и др. Если пренебречь этими потерями энергии, то можно написать, что , т.е.

. (5)

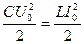
Колебания, происходящие в идеальном колебательном контуре, в котором выполняется это условие, называются свободными, или собственными, колебаниями контура.

В этом случае напряжение U (и заряд Q) на конденсаторе изменяется по гармоническому закону:

, (6)

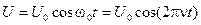
где n — собственная частота колебательного контура, w = 2pn — собственная (круговая) частота колебательного контура. Частота электромагнитных колебаний в контуре определяется как

или . (7)

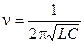
Период T – время, в течение которого совершается одно полное колебание напряжения на конденсаторе и тока в контуре, определяется формулой Томсона

. (8)

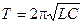
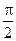
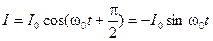
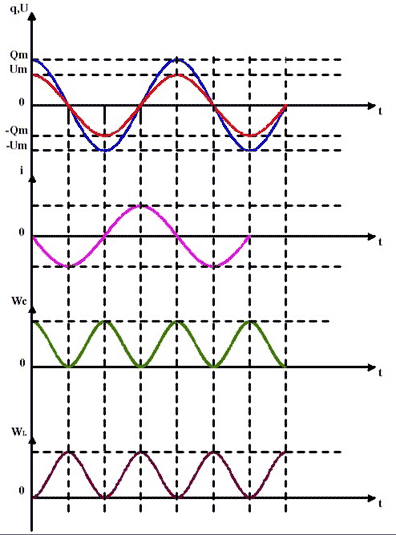
Сила тока в контуре также изменяется по гармоническому закону, но отстает от напряжения по фазе на . Поэтому зависимость силы тока в цепи от времени будет иметь вид

. (9)

На рис.6 представлены графики изменения напряжения U на конденсаторе и тока I в катушке для идеального колебательного контура.

В реальном контуре энергия с каждым колебанием будет убывать. Амплитуды напряжения на конденсаторе и тока в контуре будут убывать, такие колебания называются затухающими. В задающих генераторах их применять нельзя, т.к. прибор будет работать в лучшем случае в импульсном режиме.

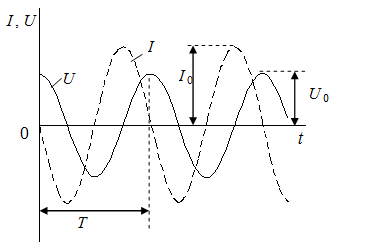Рис.5	Рис.6

Для получения незатухающих колебаний необходимо компенсировать потери энергии при самых разнообразных рабочих частотах приборов, в том числе и применяемых в медицине.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 10034 — | 7811 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

07.06.2019

5 июня Что порешать по физике

30 мая Решения вчерашних ЕГЭ по математике

Колебания напряжения на конденсаторе в цепи переменного тока описываются уравнением где все величины выражены в СИ. Емкость конденсатора равна Найдите амплитуду силы тока. (Ответ дать в амперах.)

Общий вид зависимости напряжения на конденсаторе в колебательном контуре: где — амплитудное значение напряжения. Сравнивая с находим, что Значение максимального заряда на обкладках конденсатора равно Амплитуда колебаний силы тока связана с частотой колебаний и максимальным значением заряда конденсатора соотношением Отсюда находим

Позвольте предложить, на мой взгляд, более простой способ решения. Известно, что в цепи переменного тока, в которой есть конденсатор, выполняется зависимость Im=Um/Xc, где под током и напряжением имеются ввиду их амплитудные значения, а Хс — емкостное сопротивление конденсатора, равное Хс=1/w*C. Подставляя 2-ую формулу в первую, окончательно имеем: Im=Um*w*C. Подставляя значения величин из условия, получаем значение амплитуды силы тока, которое совпадает с вашим.

P. S. Мой способ решения кажется мне более разумным по той причине, что обе формулы даны в учебнике по физике, в отличие от последней формулы в предложенном вами способе решения.

Спасибо. Хороший вариант.

Но использованная в конце формула, конечно же, дается в школьном курсе. Ведь насколько я знаю, в этот момент в школьной физике уже начинают использовать производные. Формула следует из закона изменения заряда со временем при гармонических колебаниях и из того, что ток — это производная от заряда

Видео:Зависимость силы тока от напряжения. Сопротивление. Закон Ома | Физика 8 класс #15 | ИнфоурокСкачать

Уравнение выражает зависимость силы тока от времени

Вопрос по физике:

Уравнение i=0.0001пcos(wt+п/2) выражает зависимость силы тока от времени в колебательном контуре. Чему будет равна энергия на конденсаторе и в катушке индуктивности, если ток в цепи равен 0.0001 А?

1) В конденсаторе энергия минимальна, в катушке максимальна
2) В конденсаторе и катушке энергия распределена поровну
3) В конденсаторе энергия максимальна, в катушке равна нулю
4) В конденсаторе энергия равна нулю, в катушке максимальна

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Очевидно что ответ 4) потому что Iм=0,0001A

в этот момент энергия МП максимальна а энергия ЭП равна нулю.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.

Видео:Зависимость заряда конденсатора и силы тока от времениСкачать

Уравнение зависимости силы тока от времени

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.

Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид

где q» — вторая производная заряда по времени. Величина

является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре дается формулой (Томсона):

Величина φ = ώt + φ , стоящая под знаком синуса или косинуса, является фазой колебания.

Фаза определяет состояние колеблющейся системы в любой момент времени t.

Ток в цепи равен производной заряда по времени, его можно выразить

Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,

где- угол между нормалью к рамке и вектором магнитной индукции .

По закону электромагнитной индукции Фарадея ЭДС индукции равна

где — скорость изменения потока магнитной индукции.

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции

где — амплитудное значение ЭДС индукции.

2. Если к контуру подключить источник внешней гармонической ЭДС

то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.

При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.

В промышленных цепях переменного тока России принята частота 50 Гц.

Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:

Поэтому количество теплоты, выделится за время Т:

Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:

Отсюда действующее значение тока

Аналогично действующее значение напряжения

Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.

Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.

называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего

Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.

Из уравнения следует, что . Период определим по формуле циклической частоты

Зависимость силы тока от времени имеет вид:

Амплитуда силы тока.

Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 510 3 А, ток изменяется по закону:

i=-5000 sin100t

Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока:

• Образовательные: обобщение и систематизация знаний по теме, проверка знаний, умений, навыков. В целях повышения интереса к теме работу вести с помощью опорных конспектов.
• Воспитательные: воспитание мировоззренческого понятия (причинно-следственных связей в окружающем мире), развитие у школьников коммуникативной культуры.
• Развивающие: развитие самостоятельности мышления и интеллекта, умение формулировать выводы по изученному материалу, развитие логического мышления, развитие грамотной устной речи, содержащей физическую терминологию.

Тип урока:систематизация и обобщение знаний.

Техническая поддержка урока:

• Демонстрации:
• Плакаты.
• Показ слайдов с помощью информационно – компьютерных технологий.
• Дидактический материал:
• Опорные конспекты с подробными записями на столах.
• Оформление доски:
• Плакат с кратким содержанием опорных конспектов (ОК);
• Плакат – рисунок с изображением колебательного контура;
• Плакат – график зависимости колебаний заряда конденсатора, напряжения между обкладками конденсатора, силы тока в катушке от времени, электрической энергии конденсатора, магнитной энергии катушки от времени.

План урока:

1. Этап повторения пройденного материала. Проверка домашнего задания.
Четыре группы задач по теме:

• Электромагнитные колебания.
• Колебательный контур.
• Свободные колебания. Свободные колебания – затухающие колебания
• Характеристика колебаний.

2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.

Учитель: Темой урока является «Решение задач по теме: «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ»

К доске вызываются 3 ученика для проверки домашнего задания.

– Задания по этой теме можно разделить на четыре группы.

Четыре группы задач по теме:

1. Задачи с использованием общих законов гармонических колебаний.
2. Задачи о свободных колебаниях конкретных колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.

– Мы остановимся на решении задач 1 и 2 групп.

Урок начнем с повторения необходимых понятий для данной группы задач.

Электромагнитные колебания – это периодические и почти периодические изменения заряда, силы тока и напряжения.

Колебательный контур – цепь, состоящая из соединительных проводов, катушки индуктивности и конденсатора.

Свободные колебания – это колебания, происходящие в системе благодаря начальному запасу энергии с частотой, определяемой параметрами самой системы: L, C.

Скорость распространения электромагнитных колебаний равна скорости света: С = 3 . 10 8 (м/с)

Основные характеристики колебаний

Амплитуда (силы тока, заряда, напряжения) – максимальное значение (силы тока, заряда, напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда, напряжения) – i, q, u

Схема колебательного контура

Учитель: Что представляют электромагнитные колебания в контуре?

Электромагнитные колебания представляют периодический переход электрической энергии конденсатора в магнитную энергию катушки и наоборот согласно закону сохранения энергии.

Задача №1 (д/з)

Колебательный контур содержит конденсатор емкостью 800 пФ и катушку индуктивности индуктивностью 2 мкГн. Каков период собственных колебаний контура?

Задача № 2 (д/з)

Колебательный контур состоит из конденсатора емкостью С и катушки индуктивности индуктивностью L. Как изменится период свободных электромагнитных колебаний в этом контуре, если электроемкость конденсатора и индуктивность катушки увеличить в 3р.

Задача № 3 (д/з)

Амплитуда силы тока при свободных колебаниях в колебательном контуре 100 мА. Какова амплитуда напряжения на конденсаторе колебательного контура, если емкость этого конденсатора 1 мкФ, а индуктивность катушки 1 Гн? Активным сопротивлением пренебречь.

Схема электромагнитных колебаний

Ученик 1 наглядно описывает процессы в колебательном контуре.

Ученик 2 комментирует электромагнитные колебания в контуре, используя графическую зависимость заряда, напряжения. Силы тока, электрической энергии конденсатора, магнитной энергии катушки индуктивности от времени.

Уравнения, описывающие колебательные процессы в контуре:

Обращаем внимание, что колебания силы тока в цепи опережают колебания напряжения между обкладками конденсатора на π/2.
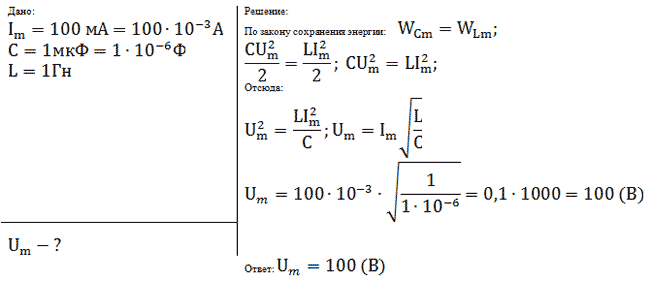
Описывая изменения заряда, напряжения и силы тока по гармоническому закону, необходимо учитывать связь между функциями синуса и косинуса.

Задача № 1.

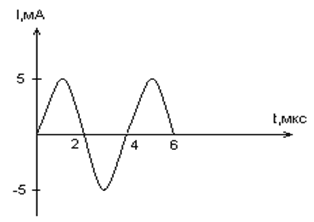
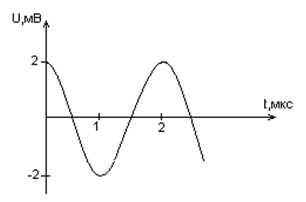
По графику зависимости силы тока от времени в колебательном контуре определите, какие преобразования энергии происходят в колебательном контуре в интервале времени от 1мкс до 2мкс?

1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.

Задача № 2.

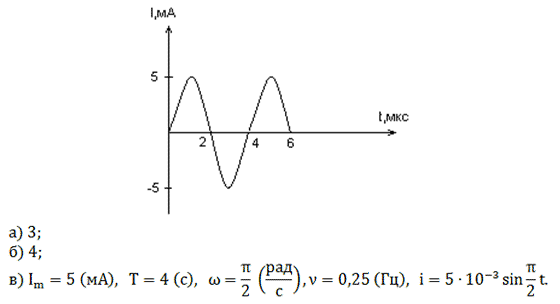
По графику зависимости силы тока от времени в колебательном контуре определите:

а) Сколько раз энергия катушки достигает максимального значения в течение первых 6 мкс после начала отсчета?
б) Сколько раз энергия конденсатора достигает максимального значения в течение первых 6 мкс после начала отсчета?
в) Определите по графику амплитудное значение силы тока, период, циклическую частоту, линейную частоту и напишите уравнение зависимости силы тока от времени.

Задача № 3 (д/з)

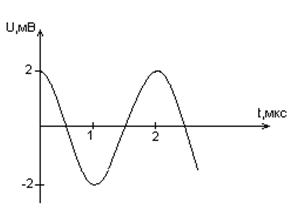
Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите, какое преобразование энергии происходит в интервале времени от 0 до 2 мкс?

1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.

Задача № 4 (д/з)

Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите: сколько раз энергия конденсатора достигает максимального значения в период от нуля до 2мкс? Сколько раз энергия катушки достигает наибольшего значения от нуля до 2 мкс? По графику определите амплитуду колебаний напряжений, период колебаний, циклическую частоту, линейную частоту. Напишите уравнение зависимости напряжения от времени.

К доске вызываются 2 ученика

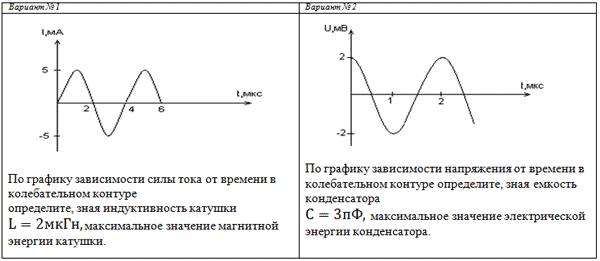
Задача № 5, 6

Задача № 7

Заряд на обкладках конденсатора колебательного контура изменяется по закону
q = 3·10 –7 cos800πt. Индуктивность контура 2Гн. Пренебрегая активным сопротивлением, найдите электроемкость конденсатора и максимальное значение энергии электрического поля конденсатора и магнитного поля катушки индуктивности.

Задача № 8

В идеальном колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменяется заряд конденсатора в колебательном контуре с течением времени.

1. Напишите уравнение зависимости заряда от времени. Найдите амплитуду колебаний заряда, период, циклическую частоту, линейную частоту.

2. Какова энергия магнитного поля катушки в момент времени t = 5 мкс, если емкость конденсатора 50 пФ.

Домашнее задание. Напишите уравнение зависимости силы тока от времени. Найдите амплитуду колебаний силы тока. Постройте графическую зависимость силы тока от времени.

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Видео:Зависимость силы тока от напряженияСкачать

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).

Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

Видео:Электрическая цепь и ее составные части. Сила тока. Напряжение. 8 класс.Скачать

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

Соотношение (1) применяется при решении многих задач.

Видео:Урок 151 (осн). Зависимость силы тока от напряжения. Закон ОмаСкачать

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1) :

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

Видео:Закон Ома для участка цепи. Электрическое сопротивление проводника. 8 класс.Скачать

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).

Рис. 10. Положительное направление обхода

Сила тока считается положительной 0)’ (I > 0)’ /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0′ I > 0′ /> , то заряд левой пластины возрастает, и потому 0′ dot > 0′ /> .

Величины и меняются со временем, но энергия контура остаётся неизменной:

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):

Подставляя сюда и , получим:

Но сила тока не является функцией, тождественно равной нулю; поэтому

Перепишем это в виде:

Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

Амплитуда силы тока равна:

Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2 ).

Ток течёт в отрицательном направлении: . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13) .

А теперь посмотрите на рис. 8 . Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!

Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

запишем закон изменения тока (13) в виде:

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .

Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).

Видео:Физика 8 класс. §42 Зависимость силы тока от напряжения.Скачать

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте .

Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Обучающее видео
БЕСПЛАТНО

Техническая поддержка:
help@ege-study.ru (круглосуточно)

Полный онлайн-курс подготовки к ЕГЭ по математике. Структурировано. Четко. Без воды. Сдай ЕГЭ на 100 баллов!

Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.

Все поля обязательны для заполнения

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Премиум

Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.

Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса — от 3,5 до 4,5 часов.

1. Уравнения (задача 13)
2. Стереометрия (задача 14)
3. Неравенства (задача 15)
4. Геометрия (задача 16)
5. Финансовая математика (задача 17)
6. Параметры (задача 18)
7. Нестандартная задача на числа и их свойства (задача 19).

Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.

Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум — репетитор-профессионал Анна Малкова.

Видео:Урок 147 (осн). Сила тока. Единицы силы тока. АмперметрыСкачать

Получи пятерку

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.

Задачи комплекта «Математические тренинги — 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.

Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.

Видео:Опыты по физике. Зависимость силы тока от напряжения на участке цепиСкачать

Как пользоваться?

1. Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
2. Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
3. Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
4. Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
5. Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.

Стоимость комплекта «Математические тренинги – 2019» — всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.

Это пробная версия онлайн курса по профильной математике.

Вы получите доступ к 3 темам, которые помогут понять принцип обучения, работу платформы и оценить ведущую курса Анну Малкову.

— 3 темы курса (из 50).
— Текстовый учебник с видеопримерами.
— Мастер-класс Анны Малковой.
— Тренажер для отработки задач.

Регистрируйтесь, это бесплатно!

Нажимая на кнопку, вы даете согласие на обработку своих персональных данных

📺 Видео

Зависимость тока от частоты и индуктивностиСкачать

Зависимость силы тока от напряженияСкачать

Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Зависимость скорости упорядоченного движения электронов от силы тока в проводникеСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

58. Сила тока при размыкании и замыкании цепиСкачать

Лабораторная работа Исследование зависимости силы тока от напряжения на участке цепиСкачать

Физика: зависимость координаты тела от времениСкачать