Уравнение второго закона ньютона для движения тела со скоростью v по круговой орбите вокруг (7 видео)

Законы движения планет и спутников

Планеты солнечной системы обращаются вокруг Солнца по орбитам, которые можно считать круговыми. Причем плоскости этих орбит почти совпадают друг с другом. Движение планет подчиняется второму закону Ньютона. Для одной из планет уравнение ее движения имеет вид

где М — масса Солнца, т — масса планеты, г — радиус орбиты. Это уравнение описывает также движение спутника Земли в том случае, когда он движется по круговой орбите.

Рис. 7.8. Движение тела т по круговой орбите под действием силы тяготения к массивному телу М

Содержание

Космические скорости
Второй закон Ньютона (Расчёты Примеры)
Что такое второй закон Ньютона, масса и вес тела
Ускорение от величины силы
Зависимость ускорения от массы
Что такое импульс
Масса тела с ростом скорости
Задачи на второй закон ньютона
Похожие страницы:
Leave a Comment
Второй закон Ньютона
Формулировка второго закона Ньютона
Использование второго закона Ньютона
Примеры задач с решением
🌟 Видео

Видео:Второй закон Ньютона. Решение задач о движении тела. Урок 8. Физика 9 класс.Скачать

Космические скорости

Запишем второй закон Ньютона для искусственного спутника Земли, движущегося но круговой орбите, радиус которой почти равен радиусу Земли R :

где т — масса спутника, М — масса Земли. Разрешим уравнение (7.9) относительно скорости спутника. Получим

При помощи формулы (7.7) это выражение можно преобразовать к вид>’

Скорость такого спутника называется первой космической скоростью. Она имеет значение 8 • 10 3 м/с.

Наименьшая скорость, которую необходимо сообщить телу на поверхности Земли для того, чтобы оно могло, преодолев ее притяжение, удалиться на бесконечно большое расстояние, называют второй космической скоростью. Ее значение можно установить при помощи закона сохранения энергии:

где v — скорость тела, когда оно находится на расстоянии г от центра Земли. Первое слагаемое в равенстве (7.12) есть кинетическая энергия тела, а второе — потенциальная энергия его взаимодействия с Землей.

Пусть телу у поверхности Земли сообщили скорость v₀. В таком случае энергия тела у поверхности Земли будет равна

На бесконечно большом расстоянии от Земли потенциальная энергия тела станет равна нулю, а скорость уменьшится до значения Vqq. Теперь энергия тела будет

Согласно закону сохранения энергии эти значения энергии равны друг другу:

Это равенство приводит к соотношению

из которого следует, что скорость v_Q принимает наименьшее значение, когда скорость тела на бесконечности равна нулю: Voo — 0. Таким образом придем к формуле для второй космической скорости

Видео:Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать

Второй закон Ньютона (Расчёты Примеры)

Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.

В результате чего были выведена новая формула второго закона ньютона а = F /m,

Видео:Три Закона Ньютона. Простое ОбъяснениеСкачать

Что такое второй закон Ньютона, масса и вес тела

Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований.

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.

Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.

Ускорение от величины силы

I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at₂) : 2 определим ускорение a.

Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку

Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m . Это отношение назовем массой тела.

Зависимость ускорения от массы

II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).

Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть

Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).

Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):

где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.

Результирующая сила F равна векторной сумме всех сил, приложенных к телу;

Следовательно, сила равна произведению массы на ускорение.

Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение

подставим это выражение в уравнение второго закона Ньютона. Получим

Что такое импульс

Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (т υ ).

Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)

Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содер жащегося в данной теле. Это определение несовершенно.

Из второго закона Ньютона вытекает следующее определение массы. Из равенства

видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость это го тела и наоборот.

Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.

Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:

где m — масса тела, движущегося со скоростью υ; m₀ — масса этого же тела, находящегося в покое; с = 3 • 10 8 м/с скорость света в вакууме.

Проанализируем данное уравнение:

Если υ«с, то величиной —, как очень малой, можно пре небречь и m = m₀, то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения;
Если υ ≈ с, то υ₂/с₂ ≈ 1, тогда т = m₀/0— отсюда вытекает, что m → ∞.

По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.

Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.

Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.

Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.

Масса тела с ростом скорости

Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.

Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.

Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).

Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ₀ = 0) называется свободным падением.

Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.

Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.

Если Р — сила тяжести, m — масса, g — ус корение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м /с 2 ), то применяя второй закон динамики, получим

Выразим с помощью этой формулы веса двух различных тел. Тогда:

Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.

Задачи на второй закон ньютона

1. Какая сила F действует на автомобиль массой кгm=1000 кг, если он движется с ускорением мсa=1 м/с 2 .

Дано:
m = 1000 кг
a = 1 м/с 2

Найти: F — ?

Решение:

Запишем второй закон Ньютона :

F = 1000 кг • 1 м/с 2 = 1000 Н

Ответ: 1000 Н.

2. На мяч действует сила F = 70 Н, масса мяча m = 0,2 кг, найти его ускорение a.

Дано:

Найти:

Решение:

Запишем второй закон Ньютона :

Статья на тему Второй закон Ньютона

Второй закон Ньютона

Следствием закона инерции является то, что тело само, без взаимодействия с другими телами не может изменить свою скорость. Любое изменения величины скорости или ее направления вызвано действием внешних тел. Данное воздействие мы характеризуем при помощи сил.

Видео:Второй закон Ньютона | Физика 9 класс #11 | ИнфоурокСкачать

Формулировка второго закона Ньютона

Второй закон Ньютона (основной закон динамики) отражает соотношение между силой и изменением скорости тел при их взаимодействии.

Самый простой вид второй закон Ньютона имеет в инерциальных системах отсчета.

Пусть скорость движения тела много меньше, чем скорость света.

И так, если тело движется с ускорением, по отношению к инерциальной системе отсчета, то на него действует сила. Сила, вызывает ускорение, величина которого пропорциональна модулю этой силы. Направление ускорения совпадает с направлением, действующей силы. При заданном ускорении сила пропорциональна массе тела, которому она сообщает ускорение. При скорости много меньшей скорости света, рассматриваемая сила не зависит от скорости движения ускоряемого тела. Более коротко можно сказать, что сила ($overline$), вызывающая ускорение тела ($overline$), в инерциальной системе отсчета пропорциональная массе ($m$) тела, умноженной на его ускорение:

Выражение (1) — это второй закон Ньютона в классической динамике.

Этот закон можно записать в иной форме:

где $overline

=moverline$ — импульс тела. Тогда второй закон Ньютона формулируют так: сила равна производной от импульса по времени — это наиболее общая формулировка основного закона динамики.

Если на тело действуют несколько сил, равнодействующая которых равна:

то второй закон Ньютона принимает вид:

Если материальная точка перемещается равномерно по окружности, то равнодействующая всех сил направлена к центру окружности, тогда равнодействующую силу называют центростремительной.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Использование второго закона Ньютона

При помощи второго закона Ньютона можно определить силы, которые действуют на тела или характер движения тела по известным силам.

При составлении уравнений движения нужно:

Определить все (или те что обязательно следует учесть) силы, которые действуют на тело (материальную точку).
Найти равнодействующую этих сил.
Записать второй закон Ньютона, составленное уравнение движения решить относительно неизвестного параметра.

Видео:ЭТО ОБЯЗАТЕЛЬНО НУЖНО ЗНАТЬ — Второй Закон Ньютона или от чего зависит ускорение телаСкачать

Примеры задач с решением

Задание. Движение материальной точки задают уравнения: $x=At^3; y=Bt$. Изменяется ли сила, действующая на точку по величине?

Решение. По второму закону Ньютона сила, действующая на точку равна:

Изменения координат материальной точки задают уравнения:

Найдем компоненты ускорения точки в соответствии с формулами:

Модуль ускорения материальной точки равен:

Получаем в соответствии с (1.1) и (1.4):

Ответ. Из выражения $F=mcdot 6At,$ следует, что величина силы увеличивается с течением времени по линейному закону.

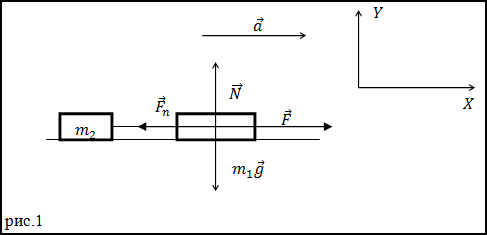
Задание. По горизонтальной очень гладкой поверхности движутся с ускорением два груза, связанные невесомой нерастяжимой нитью. Массы грузов равны $m_1 и m_2$. На первый груз действует сила F (она направлена горизонтально). Какова сила натяжения нити, которая связывает грузы? Силой трения грузов о поверхность пренебречь.

Решение. Изобразим силы, которые действуют на первый груз (рис.1).

По второму закону Ньютона запишем:

Нам потребуется для решения задачи проекция уравнения (2.1) на ось Y:

В уравнении (2.2) у нас присутствуют две неизвестные величины: сила натяжения нити ($F_n$) и ускорение тела ($a$). Для нахождения ускорения с которым движется первое тело и вся система, определим, какие силы действуют на систему, если оба тела считать одним целым. Тогда на это тело массы $m_1+m_2$ при отсутствии трения действует одна сила $overline$. В таком случае второй закон Ньютона примет вид:

В проекции на ось Y выражения (2.3) получим:

Из (2.4) ускорение тел равно:

Из (2.2) и (2.5) получим силу натяжения нити равной:

Ответ. $F_n=Fleft(1-fracright)$