- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- Анализ временных рядов
- Прогноз, характеристики и параметры прогнозирования
- Уравнение тренда временного ряда
- ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ
- Учебное пособие: Анализ временных рядов
- 1.Цели, методы и этапы анализа временных рядов
- 2.Структурные компоненты временного ряда
- 3.Модели компонентов детерминированной составляющей временного ряда
- 3.1.Модели тренда
- 3.2 Модели сезонной компоненты
- 3.3 Модель интервенции
- 4.Методы выделения тренда
- 4.1 Скользящие средние
- 4.2 Определение порядка полинома методом последовательных разностей
- 4.3.Методы экспоненциального сглаживания
- 11.Прогнозирование по модели АРИСС
- 12.Технология построения моделей АРИСС
- 🎥 Видео
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 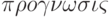
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 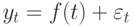

Неслучайная функция f (t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами ( t, yt ) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t ), где f (t) = a0+a1(t ).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel .
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f (t) в точках ti от значений исходного временного ряда в тех же точках ti . Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид 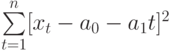
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
| t | t 2 | хt | хtt |
|---|---|---|---|
| 1 | 1 | 2 | 2 |
| 2 | 4 | 1 | 2 |
| 3 | 9 | 4 | 12 |
| 4 | 16 | 4 | 16 |
| 5 | 25 | 6 | 30 |
| 6 | 36 | 8 | 48 |
| 7 | 49 | 7 | 49 |
| 8 | 64 | 9 | 72 |
| 9 | 81 | 12 | 108 |
| 10 | 100 | 11 | 110 |
 | 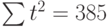 | 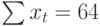 | 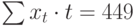 |
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f (t) имеет вид:
f (t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Временной ряд приведен в таблице. Используя средства MS Excel :
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Рассмотрим решение этой задачи средствами Microsoft Excel . При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3 рис. 14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4 рис. 14.4.
Итоговый график представлен на рисунке 14.5 рис. 14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t ), найденного по методу наименьших квадратов. Для этого в полученное для f (t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel ):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t ), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
Видео:14-02 Временной ряд как структура данныхСкачать

ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ
Краткая теория
Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.
Временной ряд – это совокупность значения какого-либо показателя за несколько последовательных моментов или периодов.
Каждый уровень временного ряда ( 



Модели, в которых временной ряд представлен как сумма перечисленных компонент,- аддитивные модели, как произведение — мультипликативными моделями временного ряда.
Аддитивная модель имеет вид: 
мультипликативная модель: 
Построение аддитивной и мультипликативной моделей сводится к расчету значений 


Построение модели включает следующие шаги:
1. выравнивание исходного ряда методом скользящей средней;
2. расчет значений сезонной компоненты 
3. устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной 

4. аналитическое выравнивание уровней 


5. расчет полученных по модели значений 

6. расчет абсолютных и/или относительных ошибок.
Автокорреляция уровней ряда – это корреляционная зависимость между последовательными уровнями временного ряда:

где 

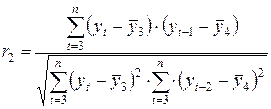
где 

Формулы для расчета коэффициентов автокорреляции старших порядков легко получить из формулы линейного коэффициента корреляции.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:
· линейная 
· гипербола 
· экспонента 
· степенная функция 
· парабола второго и более высоких порядков 
Параметры трендов определяются обычным МНК, в качестве зависимой переменной выступает время 


При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.
Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например 



Метод последовательных разностей заключается в следующем: если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями:

если параболический тренд – вторыми разностями:

В случае экспоненциального и степенного ряда метод последовательных разностей применяется к логарифмам исходных данных.
Модель, включающая фактор времени, имеет вид:

Параметры 

Автокорреляция в остатках – корреляционная зависимость между значениями остатков 
Для определения автокорреляции в остатках используют критерий Дарбина-Уотсона и расчет величины:


Коэффициент автокорреляции остатков первого порядка определятся по формуле:


Критерий Дарбина-Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением:

Эконометрические модели, содержащие не только текущие, но и лаговые значения факторных переменных, называются моделями с распределенным лагом.
Модель с распределенным лагом в предположении, что максимальная величина лага конечна, имеет вид

Коэффициент 





В момент времени 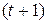






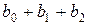


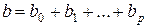
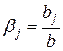

называют относительными коэффициентами модели с распределенным лагом. Если все коэффициенты 


Величина среднего лага определяется по формуле средней арифметической взвешенной
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени 
Медианный лаг — это период, в течение, которого с момента времени 


Оценку параметров модели с распределенными лагами можно проводить согласно одному из двух методов: методу Койка или методу Алмон.
В распределении Койка делается предположение, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:


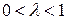
Уравнение регрессии преобразуется к виду:

В методе Алмон предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному распределению:

Уравнение регрессии примет вид:

где 


Модели, содержащие в качестве фактора лаговые значения зависимой переменной, называют моделями авторегрессии, например:

Как и в модели с распределенным лагом, 



Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.
Примеры решения задач
Пример 5.2.1.
По данным за 18 месяцев построено уравнение зависимости прибыли предприятия 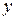



При анализе остаточных величин были использованы значения, приведенные в таблице 5.2.1.
| № |  |  |  |
| … | … | … |


1. По трем позициям рассчитать 




2. Рассчитать критерий Дарбина-Уотсона.
3. Оценить полученный результат при 5%-ном уровне значимости.
4. Указать, пригодно ли данное уравнение для прогноза.
Решение.
1. 


Остатки рассчитываются по формуле 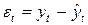




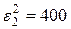



Результаты вычислений оформим в виде таблицы 5.2.2.
| № |  |  |  |  |  |  |
| — | — | — | ||||
| -50 | -70 | |||||
| … | … | … | … | … | … | … |
| ∑ |
2. Критерий Дарбина-Уотсона рассчитывается по формуле

3. Выдвигаем гипотезу 
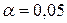


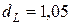

Если статистика Дарбина-Уотсона 








В данной задаче 

4. Уравнение не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь различные причины: возможно, в уравнение не включен какой-либо существенный фактор, либо неточна форма связи, а, может быть, в рядах динамики имеется общая тенденция.
Пример 5.2.2
Имеются следующие данные о величине дохода на одного члена семьи и расхода на товар А (таблица 5.2.3).
| Показатель | 1985г. | 1986г. | 1987г. | 1988г. | 1989г. | 1990г. |
| Расходы на товар А, руб. | ||||||
| Доход на одного члена, % к 1985 г. |
1. Определить ежегодные абсолютные приросты доходов и расходов и сделать выводы о тенденции развития каждого ряда.
2. Перечислить основные пути устранения тенденции для построения модели спроса на товар А в зависимости от дохода.
3. Построить линейную модель спроса, используя первые разности уровней исходных динамических рядов.
4. Пояснить экономический смысл коэффициента регрессии.
5. Построить линейную модель спроса на товар А, включая в нее фактор времени. Интерпретировать полученные параметры.
Решение.
1. Обозначим расходы на товар А через 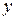



Расчеты можно оформить в виде таблицы (табл. 5.2.4).
 |  |  | 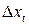 |
| — | — |
Значения 

2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар А необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, т.е. 
Другой возможный путь учета тенденции при построении модели — найти по каждому ряду уравнение тренда:
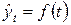
и отклонения от него:
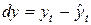
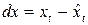
Далее модель строится по отклонениям от тренда:

При построении эконометрических моделей чаще используется другой путь устранения тенденции – включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельно фактора включается время, т.е. 
3. Модель имеет вид

Для определения параметров 

Применительно к нашим данным имеем
Решая эту систему, получим 


4. Коэффициент регрессии 
5. Модель имеет вид

Применяя МНК, получим систему нормальных уравнений:
Применительно к нашим данным, система примет вид:
Решая ее, получим 


Уравнение регрессии имеет вид

Параметр 
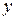


Пример 5.2.3.
По данным за 18 месяцев некоторого временного ряда 









Для прогнозирования значений 
Решение.
Наиболее целесообразно построение уравнения авторегрессии вида:

так как значение 
Кроме того, возможно построение и множественного уравнения авторегрессии 



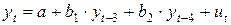
Сравнить полученные уравнения и выбрать наилучшее решение можно с помощью скорректированного коэффициента детерминации.
Пример 5.2.4.
На основе помесячных данных о потреблении электроэнергии в регионе (млн. кВт∙ч) за последние три года была построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за соответствующие месяцы приводятся ниже:
| январь | +25 | май | -32 | сентябрь | +2 |
| февраль | +10 | июнь | -38 | октябрь | +15 |
| март | +6 | июль | -25 | ноябрь | +27 |
| апрель | -4 | август | -18 | декабрь | ? |
Уравнение тренда выглядит следующим образом:
(при расчете параметров тренда для моделирования переменной времени использовались натуральные числа 
1. Определите значение сезонной компоненты за декабрь.
2. На основе построенной модели дайте точечный прогноз потребления электроэнергии на первый квартал следующего года.
Решение.
1. Сумма значений сезонной компоненты внутри одного цикла должна быть равна нулю (в соответствии с методикой построения аддитивной модели временного ряда). Следовательно, значение сезонной компоненты за декабрь составит:

2. Прогнозное значение уровня временного ряда 


Ожидаемое потребление электроэнергии за первый квартал следующего года есть сумма ожидаемого потребления электроэнергии за январь 


Для расчета трендовых значений воспользуемся уравнением тренда:


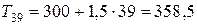
Соответствующие значения сезонной компоненты составят


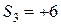
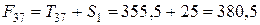
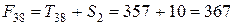
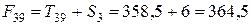
Ожидаемое потребление электроэнергии за первый квартал следующего года в регионе составит 
При исследовании капитальных расходов от капитальных ассигнований была получена модель:
где 






Задание.
Выпишите краткосрочный, долгосрочный и промежуточные мультипликаторы в данной модели. Определите средний и медианный лаг. Поясните смысл этих показателей.
Решение.
Рассматриваемое уравнение представляет собой модель с распределенными лагами вида:

Коэффициент 





В момент времени 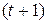










Для максимального лага 

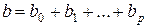





Для определения среднего и медианного лага нам потребуется рассчитать относительные коэффициенты, которые определяются по формуле:
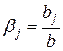



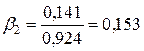
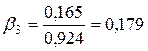



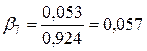
Величина среднего лага определяется по формуле средней арифметической взвешенной
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени 

Медианный лаг-это период, в течение, которого с момента времени 


Так как 

Пример 5.2.6.
На основе помесячных данных за последние 20 лет изучается зависимость между уровнем дивидендов по обыкновенным акциям 

1) результаты аналитического выравнивания рядов:
тренд в форме параболы второго порядка
а) для ряда 

б) для ряда 


а) для ряда 


б) для ряда 


2) коэффициенты корреляции:
по исходным уровням рядов -0,98;
по отклонениям от параболического тренда- 0,78;
по отклонениям от линейных трендов-0,45;
по первым разностям – 0,42;
по вторым разностям -0,76.
Задание.
1. Есть ли взаимосвязь между исследуемыми временными рядами? Если есть, то укажите количественную характеристику взаимосвязи между исследуемыми временными рядами. Ответ обоснуйте.
2. Поясните причины различия полученных мер тесноты связи.
Решение.
1. Высокие коэффициенты детерминации, полученные при построении параболических трендов по исходным уровням временных рядов, указывают на нарушение условия стационарности, то есть исходные временные ряды характеризуются параболической тенденцией. Следовательно, уравнение регрессии следует строить не по исходным уровням временных рядов, а по вторым разностям или по отклонениям от параболического тренда. Из условия задачи видно, что коэффициенты корреляции для уравнений регрессии, построенных по вторым разностям и по отклонениям от параболического тренда высоки (0,84 и 0,78 соответственно), что говорит о том, что между исходными временными рядам действительно существует тесная связь. Количественной характеристикой этой связи можно считать коэффициент корреляции для уравнения регрессии, построенного по вторым разностям 0,84.
2. Коэффициент корреляции, полученный по исходным уровням 0,98, дает завышенную оценку тесноты связи между исследуемыми признаками, поскольку на него оказывает влияние сильная тенденция исходных временных рядов.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
1. Что такое эконометрика? Что является предметом изучения эконометрики? Назовите основные задачи эконометрики.
2. Что такое парная регрессия? Что такое парная линейная регрессия? Какие классы нелинейных регрессий вызнаете? Приведите примеры.
3. В чем заключается метод наименьших квадратов (МНК)?
4. По совокупности 30 предприятий торговли строится модель вида 







5. По совокупности 25 предприятий торговли изучается зависимость между признаками: 



6. Как произвести оценку качества построенной парной регрессии? Допустимый предел?
7. Для продукции вида А модель зависимости удельных постоянных расходов от объема выпускаемой продукции выглядит следующим образом: 
Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Учебное пособие: Анализ временных рядов
| Название: Анализ временных рядов Раздел: Рефераты по экономико-математическому моделированию Тип: учебное пособие Добавлен 22:56:54 22 марта 2011 Похожие работы Просмотров: 14588 Комментариев: 22 Оценило: 6 человек Средний балл: 4.2 Оценка: 4 Скачать | |
 |  |


Следовательно, выражение (2) есть

поделив (3) на 

Тот факт, что автокорреляционная функция процесса СС(q) имеет конечную протяженность (q тактов) – характерная особенность такого процесса. Если 

Как уже отмечалось, обратимые процессы СС можно рассматривать как бесконечные АР- процессы -АР(¥). Следовательно, частная автокорреляцонная функция процесса СС(р ) имеет бесконечную протяженность. Итак, у процесса СС(q ) автокорреляционная функция обрывается на лаге q , тогда как частная автокорреляционная функция плавно спадает.
10.1.5 Комбинированные процессы авторегрессии — скользящего среднего
Хотя модели АР(р ) и СС(q ) позволяют описывать многие реальные процессы, число оцениваемых параметров может оказываться значительным. Для достижения большей гибкости и экономичности описания при подборе моделей к наблюдаемым временным рядам весьма полезными оказались смешанные модели, содержащие в себе и авторегрессию и скользящее среднее. Эти модели были предложены Боксом и Дженкинсом и получили название модели авторегрессии — скользящего среднего (сокращенно АРСС(р, q )):

С использованием оператора сдвига В модель (1) может быть представлена более компактно:


где а (В )—авторегрессионный оператор порядка р ,
b (В )—оператор скользящего среднего порядка q .
Модель (
Рассмотрим простейший смешанный процесс АРСС(1,1)
Согласно

Из соотношения (2) видно, что модель АРСС(1,1) является частным случаем общей линейной модели ( ) с коэффициентами 
Из (2) легко получить выражение для дисперсии 
Для получения корреляционной функции воспользуемся тем же приемом, что и при анализе моделей авторегрессии. Умножим обе части модельного представления процесса АРСС(1,1)
на 
или (с учетом того, что второе слагаемое в правой части равенства равно нулю)
Поделив ковариации 

полученные соотношения показывают, что 






Отсюда следует, что для значений 
В итоге оказывается, что при q p будет q — p значений 
10.1.6 Интегрированная модель авторегрессии- скользящего среднего
Модель АРСС допускает обобщение на случай, когда случайный процесс является нестационарным. Ярким примером такого процесса являются «случайные блуждания»:

С использованием оператора сдвига модель (1) принимает вид

Из (2) видно, что процесс (1) расходящийся, поскольку


В общем случае полагается, что нестационарный авторегрессионный оператор 



где a (B ) – стационарный оператор авторегрессии порядка р (с корнями вне единичного круга).
Введем оператор разности 



где b (B ) – обратимый оператор скользящего среднего (вне его корни лежат вне единичного круга).
Для разности 

описывает уже стационарный обратимый процесс АРСС(р, q ).
Для того чтобы от ряда разностей вернуться к исходному ряду требуется оператор s , обратный 
Этот оператор называют оператором суммирования, поскольку

Если же исходной является разность порядка d , то для восстановления исходного ряда понадобится d — кратная итерация оператора s , иначе d — кратное суммирование (интегрирование). Поэтому процесс (3) принято называть процессом АРИСС, добавляя к АРСС термин интегрированный. Кратко модель (3) записывают как АРИСС(р, d , q ), где р – порядок авторегрессии, d – порядок разности, q – порядок скользящего среднего. Ясно, что при d =0 модель АРИСС переходит в модель АРСС .
На практике d обычно не превышает двух, то есть d .
Модель АРИСС допускает представление, аналогичное общей линейной модели, а так же в виде «чистого » процесса авторегрессии (бесконечного порядка). Рассмотрим, к примеру, процесс АРИСС (1, 1, 1):

Из (4) следует, что

В выражении (5) коэффициенты, начиная с третьего, вычисляются по формуле 
Представление (5) интересно тем, что веса, начиная с третьего, убывают по экспоненциальному закону. Поэтому, хотя формально 
Видео:Эконометрика. Моделирование временных рядов. Построение аддитивной модели.Скачать

11.Прогнозирование по модели АРИСС
Как уже отмечалось, процессы АРИСС допускают представление в виде обобщенной линейной модели, то есть
Естественно искать будущее (прогнозное) значение ряда в момент 
Ожидаемое значение 

Первая сумма в правой части последнего соотношения содержат лишь будущие возмущения (прогноз делается в момент t , когда известны прошлые значения и ряда 



Ошибка прогноза, представляющая расхождение между прогнозным значением и его ожиданием есть

Дисперсия ошибки отсюда есть

Прогнозирование по соотношению (1) в принципе возможно, однако затруднительно поскольку требует знания всех прошлых возмущений. К тому же для стационарных рядов скорость затухания 

Поскольку модель АРИСС допускает и другие представления, рассмотрим возможности их использования для прогнозирования. Пусть модель задана непосредственно разностным уравнением

По известным значениям ряда (результатам наблюдений) 

—
При прогнозировании на два такта следует вновь воспользоваться рекуррентным соотношением (3), где в качестве наблюденного значения ряда в момент t +1 следует взять предсказанную по (4) величину 

Наконец, возможно прогнозирование опираясь на представление процесса АРИСС в виде авторегрессии (). Как уже отмечалось, несмотря на то что порядок авторегрессии бесконечен, весовые коэффициенты в представлении ряда убывают довольно быстро, поэтому для вычисления прогноза достаточно умеренное число прошлых значений ряда.
Дисперсия ошибки прогноза на 
и согласно выражению (2) дается выражением
В предположении, что случайные возмущения являются гаусовским белым шумом, то есть 
Видео:Анализ и моделирование структурных изменений временного ряда ● ЭКОНОМЕТРИКА в EViews ● Лаб. работа 5Скачать

12.Технология построения моделей АРИСС
Описанные выше теоретические схемы строились в предположении, что временной ряд имеет бесконечную предысторию, тогда как реально исследователю доступен ограниченный объем наблюдений. Модель приходится подбирать экспериментально, подгоняя ее к имеющимся в распоряжении данным. Поэтому с позиций теоретического применения теории анализа временных рядов определяющее значение имеют вопросы корректной спецификации модели АРИСС(p , d , q ) (ее идентификации) и последующего оценивания ее параметров.
На этапе идентификации наблюденные данные используются для определения подходящего класса моделей и делаются предварительные оценки ее параметров, то есть строится пробная модель. Затем пробная модель подгоняется к данным более тщательно; при этом первичные оценки, полученные на этапе идентификации выступают в качестве начальных значений в итеративных алгоритмах оценивания параметров. И наконец, на третьем этапе полученная модель подвергается диагностической проверке для выявления возможной неадекватности модели и выработки подходящих изменений в ней.Рассмотрим перечисленные этапы подробнее.
Цель идентификации – получить некоторое представление о величинах p , d , q и о параметрах модели. Идентификация модели распадается на две стадии
1. Определение порядка разности d исходного ряда 
2. Идентификация модели АРСС для ряда разностей 
Основной инструмент, используемый на обеих стадиях – автокорреляционная и частная автокорреляционная функции.
В теоретической части мы видели, что у стационарных моделей автокоррелящии 
Построив коррелограмму для ряда разностей, вновь повторяют анализ и так далее. Считается, что порядок разности d , обеспечивающий стационарность, достигнут тогда, когда автокорреляционная функция процесса 

После того как будет получен стационарный ряд разностей, порядка d, изучают общий вид автокорреляционной и частной автокорреляционной функций этих разностей. Опираясь на теоретические свойства этих функций можно выбрать значения p и q для АР и СС операторов. Далее при выбранных p и q строятся начальные оценки параметров авторегрессии 






Для смешанных процессов АРСС процедура оценивания усложняется . Так для рассмотренного в п. процесса АРСС(1,1) параметры 



В общем случае вычисление начальных оценок процесса АРСС(p , q ) представляет многостадийную процедуру и здесь не рассматривается. Отметим только, что для практики особый интерес имеют АР и СС процессы 1-го и 2-го порядков и простейший смешанный процесс АРСС(1,1).
В заключение заметим, что оценки автокорреляций, на основе которых строятся процедуры идентификации могут иметь большие дисперсии (особенно в условиях недостаточного объема выборки – несколько десятков наблюдений) и быть сильно коррелированны. Поэтому говорить о строгом соответствии теоретической и эмпирической автокорреляционных функций не приходится. Это приводит к затруднениям при выборе p , d , q , поэтому для дальнейшего исследования могут быть выбраны несколько моделей.
🎥 Видео
15-09 Классификация на основе временных рядовСкачать

#ЦМФ Как выделить цикл, тренд и сезонность? Декомпозиция временного рядаСкачать

Быстрое прогнозирование в Microsoft ExcelСкачать
Временные ряды. Аддитивная и мультипликативная моделиСкачать

Statistica 10. Спектральный анализ Фурье или о том как узнать период сезонности временного рядаСкачать

Машинное обучение. Прогнозирование временных рядов. К.В. Воронцов, Школа анализа данных, Яндекс.Скачать


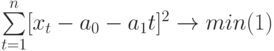
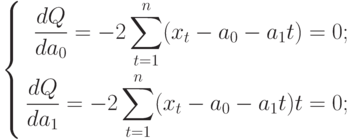
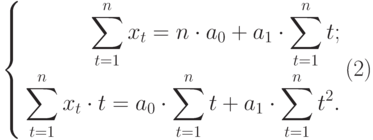
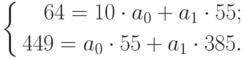




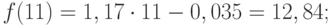
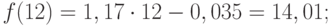
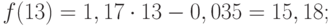
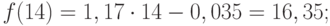
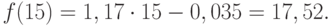

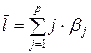











 понимают числовую последовательность
понимают числовую последовательность  , элементы которой вычисляются по определенному правилу как функция времени t . Исключив детерминированную составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может в одном предельном случае представлять чисто случайные скачки, а в другом – плавное колебательное движение. В большинстве случаев будет нечто среднее: некоторая иррегулярность и определенный систематический эффект, обусловленный зависимостью последовательных членов ряда.
, элементы которой вычисляются по определенному правилу как функция времени t . Исключив детерминированную составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может в одном предельном случае представлять чисто случайные скачки, а в другом – плавное колебательное движение. В большинстве случаев будет нечто среднее: некоторая иррегулярность и определенный систематический эффект, обусловленный зависимостью последовательных членов ряда.
 ;
; ,
, — значение ряда в момент t ;
— значение ряда в момент t ; — значение детерминированной составляющей;
— значение детерминированной составляющей; — значение случайной составляющей.
— значение случайной составляющей. ,
, ,
,


 ,
, .
.


 .
. .
.
 , для любого t , где t — период сезонности.
, для любого t , где t — период сезонности. .
. модель сезонного эффекта можно записать как
модель сезонного эффекта можно записать как ,
, — булевы, иначе индикаторные, переменные, по одной на каждый такт внутри периода t сезонности. Так, для ряда месячных данных
— булевы, иначе индикаторные, переменные, по одной на каждый такт внутри периода t сезонности. Так, для ряда месячных данных  =0 для всех t , кроме января каждого года, для которого
=0 для всех t , кроме января каждого года, для которого  при
при  — отклонение февральских значений и так далее до
— отклонение февральских значений и так далее до  . Чтобы снять неоднозначность в значениях коэффициентов сезонности
. Чтобы снять неоднозначность в значениях коэффициентов сезонности  , вводят дополнительное ограничение, так называемое условие репараметризации, обычно
, вводят дополнительное ограничение, так называемое условие репараметризации, обычно .
.


 .
. ,
, ,
, ,
,  .
.
 ,
, — значение детерминированной компоненты ряда, описываемой как интервенция;
— значение детерминированной компоненты ряда, описываемой как интервенция; — коэффициенты типа авторегрессии;
— коэффициенты типа авторегрессии; — коэффициенты типа скользящего среднего;
— коэффициенты типа скользящего среднего; — экзогенная переменная одного из двух типов;
— экзогенная переменная одного из двух типов; («ступень»), или
(«ступень»), или  («импульс»)
(«импульс») — фиксированный момент времени, называемый моментом интервенции.
— фиксированный момент времени, называемый моментом интервенции.

 .
. находим методом наименьших квадратов:
находим методом наименьших квадратов: .
. :
:
 ;
; ;
; .
.
 ;
;

 ;
;
 ;
;

 .
.
 (1)
(1) , которые в силу симметрии можно записать короче:
, которые в силу симметрии можно записать короче: .
.

 .
. . Пусть имеются, например, наблюдения на последний день каждого месяца с января по декабрь. Простое усреднение 12 точек с весами
. Пусть имеются, например, наблюдения на последний день каждого месяца с января по декабрь. Простое усреднение 12 точек с весами  дает значение тренда в середине июля. Чтобы получить значение тренда на конец июля надо взять среднее значение тренда в середине июля и середине августа. Оказывается, это эквивалентно усреднению 13-месячных данных, но значения на краях интервала берут с весами
дает значение тренда в середине июля. Чтобы получить значение тренда на конец июля надо взять среднее значение тренда в середине июля и середине августа. Оказывается, это эквивалентно усреднению 13-месячных данных, но значения на краях интервала берут с весами  . Итак, если интервал сглаживания содержит четное число 2m точек, в усреднении задействуют не 2m , а 2m +1 значений ряда :
. Итак, если интервал сглаживания содержит четное число 2m точек, в усреднении задействуют не 2m , а 2m +1 значений ряда : .
. .
. и
и  .
. .
.
 0 1 8 27 64 125
0 1 8 27 64 125 1 7 19 37 61
1 7 19 37 61 6 12 18 24
6 12 18 24 6 6 6
6 6 6 0 0
0 0 ;
; ;
; ;
; ;
; .
. .
. и т.д. и обнаружения момента , когда это отношение становится постоянным. Таким образом мы получаем оценки порядка полинома , содержащегося в исходном ряде, и дисперсии случайного компонента.
и т.д. и обнаружения момента , когда это отношение становится постоянным. Таким образом мы получаем оценки порядка полинома , содержащегося в исходном ряде, и дисперсии случайного компонента.
 и т.д. Так как сумма весов должна равняться единице, т.е.
и т.д. Так как сумма весов должна равняться единице, т.е.  , весами фактически будут
, весами фактически будут  и т.д. ( предполагается , что 0 yt+1 yt-1 > yt yt+1 или yt-1 > yt q .
и т.д. ( предполагается , что 0 yt+1 yt-1 > yt yt+1 или yt-1 > yt q . (1)
(1) .)
.)

 равны нулю в силу некоррелированности возмущений в разные моменты времени. Для нахождения автокорреляционной функции процесса СС(q ) последовательно умножим (1) на
равны нулю в силу некоррелированности возмущений в разные моменты времени. Для нахождения автокорреляционной функции процесса СС(q ) последовательно умножим (1) на  и возьмем математическое ожидание
и возьмем математическое ожидание (2)
(2)


























