Солнечные часы принципиально отличаются от всех остальных инструментов измерения времени. Дело в том, что они измеряют не одинаковые промежутки времени, как это делают все остальные часы, а движение Солнца, что не одно и то же. Разница между средним временем и солнечным описывается уравнением времени и составлет около ±15 минут.

- Среднее время и фантомное Солнце
- Эллиптическая орбита и законы Кеплера
- График уравнения времени
- Аналемматическая кривая
- Уравнение времени для солнечных часов
- 9.1. Звездное время
- 9.2. Истинное солнечное время
- 9.3. Среднее солнечное время
- 9.4. Эфемеридное время
- 9.5. Атомное время
- 9.6. Системы счета времени
- 9.7. Связь среднего времени со звездным
- 9.8. Календарь
- 9.8.1. Юлианский календарь
- 9.8.2. Григорианский календарь
- 9.9. Линия перемены даты
- 9.10. Юлианские дни
- Уравнение времени
- Уравнение времени
- Истинное солнечное время
- Причины неравномерности истинного солнечного времени
- Наклон земной оси
- Эксцентриситет орбиты Земли
- Среднее время, Историческая справка
- Уравнение времени
- 📸 Видео
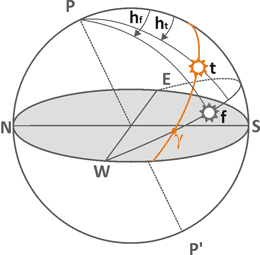
Среднее время и фантомное Солнце
Все часы кроме солнечных отмеряют одинаковые промежутки времени и показывают среднее время. Промежутками могут быть часы, минуты, секунды или миллисекунды. Чем меньше разница между двумя одинаковыми отмеренными промежутками, тем часы точнее и, стало быть, лучше. Если бы Солнце уподобилось точным часам, то оно должно было бы вращаться вокруг Земли с постоянной скоростью по круговой орбите, расположенной в плоскости экватора. В последующих рассуждениях такое Солнце будет называться фантомным и обозначаться на чертежах серым цветом и буквой f. Все наши современные представления о времени и сама система его подсчета основаны на движении этого самого фантомного Солнца, которое обращается вокруг Земли с постоянной скоростью 24 часа в сутки. И происходит это каждый день в течение всего года. Однако в реальности орбита, по которой Солнце вращается вокруг Земли, эллиптическая, а не круговая. К тому же ось вращения Земли наклонена к плоскости вращения Солнца (эклиптике) под углом около 23,5°. Именно эти два фактора приводят к тому, что реальное Солнце t ведет себя по-другому и, наряду с фантомным средним временем, существует истинное время, которое умеют показывать только солнечные часы.
На рисунке, приведенном выше, обозначены два положения Солнца, соответствующие одному моменту времени. Фантомное Солнце f всегда движется по экватору с постоянной скоростью. Среднее местное время, которое соответствует его положению, определяется углом hf, который откладывается от направления на юг, то есть полудня. В тоже время реальное Солнце t движется по эклиптике, которая пересекает экватор только в дни равноденствия. На рисунке эклиптика и реальное Солнце обозначены оранжевым цветом, а точка весеннего равноденствия буквой γ. Истинное время соответствует углу ht. В общем случае эти углы не совпадают, и уравнение времени можно записать, как ht — hf. Описанное несоответствие среднего времени истинному имеет 6-месячный период и равняется нулю четыре раза в год: в дни равноденствия и солнцестояния. За счет фактора несоответствия эклиптики экватору (то есть из-за наклона земной оси) уравнение времени изменяется примерно от -9,87 до +9,87 минут в течение года.
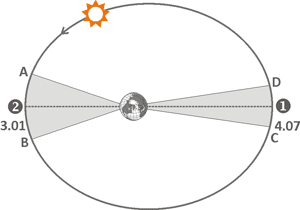
Эллиптическая орбита и законы Кеплера
Вторая причина несоответствия среднего времени истинному, то есть уравнения времени, заключается в том, что годовое движение Солнца вокруг Земли происходит по эллиптической, а не круговой орбите.
В начале XVII века немецкий астроном Иоганн Кеплер открыл три закона вращения планет, из которых к уравнению времени имеют отношение первые два. Первый закон описывает все возможные орбиты движения небесных тел относительно друг друга. В частности, при огибании Солнцем Земли по эллиптической орбите Земля располагается в одном из фокусов данного эллипса, как изображено на рисунке слева. При этом точка 1 соответствует максимальному удалению Солнца от Земли и называется апогей. Минимальное расстояние между Землей и Солнцем достигается в точке 2, называемой перигей. Ближе всего Солнце подходит к Земле 3 января, а дальше всего находится 4 июля.
Конечно, Солнце находится в одном из фокусов эллиптической орбиты, по которой Земля вращается вокруг него, но с точки зрения гномоники этот факт лишь затрудняет понимание принципов работы солнечных часов. Для тех, кто предпочитает рассматривать вращение Земли вокруг Солнца, следует заметить, что ближайшая к Солнцу точка называется перигелий, а самая удаленная — афелий.
Второй закон Кеплера утверждает, что при движении Солнца по эллиптической орбите его скорость не будет постоянной, а будет увеличиваться при приближении к Земле в точке перигея и уменьшаться в точке апогея. Саму зависимость можно проиллюстрировать графически. Солнце проходит участки AB и CD за одно и то же время в том случае, если площади соответствующих затемненных участков равны.
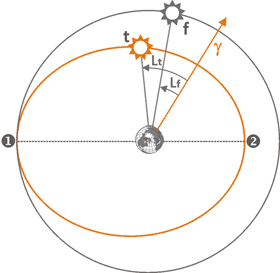
На рисунке слева изображены положения двух Солнцев: фантомного f и истинного t. Фантомное Солнце, определяющее среднее время, двигается вокруг Земли по круговой орбите с постоянной скоростью. Реальное Солнце, напротив, ускоряется возле точки перигея 2 и замедляется в апогее 1. Соответственно, долгота фантомного и реального Солнца, которая выражается углом, отложенным от точки весеннего равноденствия γ, будет разной. Доля данного несоответствия среднего времени истинному в уравнении времени выражается формулой Lt — Lf. Дважды в год, в апогее и перигее, эта разница становится равной нулю, а в остальное время она изменяется от -7,66 до +7,66 минут.
На приведенных рисунках эллиптичность орбиты намеренно подчеркнута, хотя на самом деле эксцентриситет земной орбиты составляет всего лишь 0, 017. Это означает, что орбита почти совпадает с окружностью, у которой эксцентриситет равен 0. Однако, это «почти» вносит серьезные изменения в скорость движения Солнца по эклиптике. В январе его скорость составляет 1°01′ за 24 часа против 0°57′ в июле.
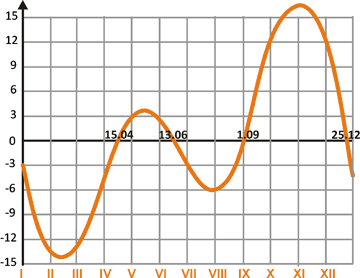
График уравнения времени
Таким образом, уравнение времени в основном складывается из двух несоответствий между временем средним и истинным, то есть солнечным. Первое несоответствие связано с наклоном земной оси. А второе несоответствие проистекает из того, что Солнце движется не по круговой, а по эллиптической орбите. Поскольку сами несоответствия сложно синхронизированы и имеют разные значения, то результирующий график уравнения времени, изображенный на рисунке в начале, несимметричен относительно нулевого значения. Уравнение времени принимает положительное значение, когда Солнце пересекает локальный меридиан раньше, чем это сделало бы фантомное Солнце, двигающееся равномерно по среднему времени. Отрицательное значение означает, что истинное время опаздывает по сравнению со средним. Как видно на графике значение уравнения времени равно нулю четыре раза в год: 15 апреля, 13 июня, 1 сентября и 25 декабря. Иногда график уравнения времени рисуют инвертированным и уравнение времени представляется, как среднее время минус истинное.
Вообще-то несоответствий между Солнцем фантомным и реальным значительно больше (известный популиризатор астрономии Фламарион описал еще 13 сложных движений Земли), но основной и заметный вклад в уравнение времени связан с орбитой Земли и наклоном оси ее вращения .
Аналемматическая кривая
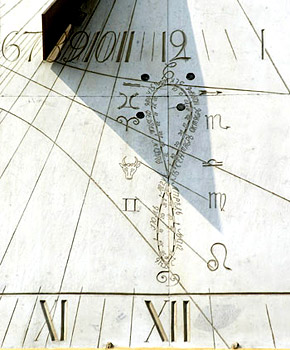
Иногда уравнение времени изображают в виде аналемматической «восьмерки». В интернете можно найти фотографии, подобные размещенной. Если установить фотоаппарат на штатив и производить мультиэкспозиционную съемку каждый день в одно и тоже гражданское время, то Солнце в течение года опишет фигуру, которая похожа на восьмерку. Именно такую фигуру называют аналеммой. В зависимости от места и времени съемки кривая может иметь разную форму и наклон. Например, если бы съемка велась в 12:00 в Гринвиче, то аналемма располагалась бы строго вертикально.
Иногда на солнечных часах изображают аналемматическую восьмерку, которая позволяет согласовать среднее и истинное время. Для этого надо знать, что полдень по среднему времени наступает, когда тень от конца гномона пересекает соответствующую часть аналеммы. Одновременно по этой тени можно определить время года, как это предполагается на часах МГУ на фотографии.
Если делаются солнечные часы, которые показывают точное среднее время, то при их разметке следует учитывать уравнение времени. Поэтому часовые линии на таких часах всегда будут в виде аналемматических кривых. Другой способ отображения среднего времени солнечными часами запечатлен на фотографии. Армилярная полусфера имеет необычный гномон в виде прорезанной аналемматической восьмерки. На изогнутой шкале представлены два времени: гражданское среднее сверху и истинное солнечное снизу.
Видео:Горизонтальные солнечные часыСкачать

Уравнение времени для солнечных часов
Единицей измерения времени в астрономии служат сутки — промежуток времени, в течение которого Земля делает полный оборот вокруг своей оси относительно какой-нибудь точки на небе. В зависимости от этой точки отсчета различают звездные сутки — промежуток времени между двумя последовательными одноименными кульминациями точки весеннего равноденствия, и истинные солнечные сутки — промежуток времени между двумя последовательными одноименными кульминациями центра Солнца. Солнечные сутки примерно на 4 минуты длиннее звездных, так как Солнце двигается среди звезд в сторону вращения Земли, и для того, чтобы его догнать, Земле надо сделать относительно звезд чуть больше одного оборота. Для измерения больших промежутков времени используют тропический год — промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия.
Для измерения времени можно использовать как звездные, так и истинные солнечные сутки. Если используются звездные сутки, измеряемое время называют звездным временем, а если истинные солнечные сутки — то истинным солнечным временем. Однако это не означает, что мы измеряем два каких-то независимых друг от друга времени. Фактически, это как бы две разные линейки для измерения времени. Так, расстояние между городами можно выразить и в километрах, и в милях. Ситуация с измерением времени та же самая.
Видео:Что такое "уравнение времени"?Скачать

9.1. Звездное время
За начало звездных суток на данном географическом меридиане принимается момент верхней кульминации точки весеннего равноденствия. Звездное время — время, протекшее с момента верхней кульминации точки весеннего равноденствия до любого другого ее положения, выраженное в долях звездных суток (звездные часы, минуты и секунды). Таким образом, звездное время s равно по величине часовому углу точки весеннего равноденствия, или сумме часового угла какого либо светила O и его прямого восхождения (см. рис. 17):
 | (11) |
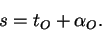 | (12) |
Отсюда, в частности, следует, что в момент верхней кульминации какой-либо звезды O звездное время в точности равно ее прямому восхождению 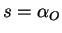
 |
Рис. 17. Связь звездного времени s с прямым восхождением 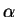 и часовым углом t светила и часовым углом t светила |
Видео:Солнечные часы: как определить время по солнцу | История часов | Познавательное видеоСкачать

9.2. Истинное солнечное время
За начало истинных солнечных суток принимается момент нижней кульминации центра Солнца. Истинное солнечное время 
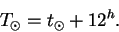 | (13) |
К сожалению, продолжительность истинных солнечных суток различна в течение года, т.к.:
1) Солнце движется не по небесному экватору, а по наклонной к нему эклиптике, т.е. изменение прямого восхождения Солнца за один день вблизи солнцестояний больше, чем вблизи равноденствий. Поэтому между нижними кульминациями Солнца вблизи солнцестояний и равноденствий проходят немного разные промежутки времени.
2) Солнце и по эклиптике двигается неравномерно из-за эллиптичности орбиты Земли.
По этим причинам, например, истинные солнечные сутки 22 декабря приблизительно на 50 секунд длиннее, чем 23 сентября. Понятно, что использование истинного солнечного времени неудобно, и поэтому было введено среднее солнечное время.
Видео:Находим время истинного солнечного полдняСкачать

9.3. Среднее солнечное время
Были введены две фиктивные точки — среднее эклиптическое Солнце и среднее экваториальное Солнце. Среднее эклиптическое Солнце равномерно двигается по эклиптике и совпадает с истинным в момент прохождения Землей перигелия. Среднее экваториальное Солнце двигается равномерно по экватору со средней скоростью истинного Солнца и одновременно со средним эклиптическим Солнцем проходит точку весеннего равноденствия.
Средние солнечные сутки — промежуток времени между двумя последовательными нижними кульминациями среднего экваториального Солнца на одном и том же географическом меридиане. За начало солнечных суток принимается нижняя кульминация среднего экваториального Солнца, и среднее солнечное время TM равно
| TM = tM + 12 h , | (14) |
где tM — часовой угол среднего экваториального Солнца.
Понятно, что среднее солнечное время нельзя непосредственно измерить из астрономических наблюдений, его можно только вычислить. Связь между истинным солнечным временем и средним солнечным временем выражается через уравнение времени 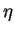
 | (15) |
Заметим, что уравнение времени можно определить не только как разность между средним и истинным солнечным временем, но и наоборот, как разницу между истинным и средним солнечным временем. В Астрономическом Ежегоднике используется второе определение, но мы, вслед за Воронцовым-Вельяминовым, будем использовать первое. Значение 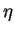
 |
Рис. 18. Изменение уравнения времени 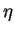 в течение года в течение года |
Видео:Солнечные часы (by daybit)Скачать

9.4. Эфемеридное время
Наблюдения показали, что и средние сутки не являются постоянной величиной. Причина — неравномерность вращения Земли вокруг своей оси. Существует вековое замедление вращения Земли из-за приливного трения, сезонные изменения, связанные с перераспределением воздушных и водяных масс на поверхности Земли. Обнаружены и нерегулярные, скачкообразные изменения скорости Земли, причина которых неизвестна. Величина этих неравномерностей — тысячные доли секунды.
Поэтому было введено равномерное эфемеридное время, которое определяется по движению Луны и планет. В 1956 г. Международный комитет мер и весов принял за основу эфемеридного времени эфемеридную секунду, как 1/31 556 925.9747 часть тропического года на 12 часов эфемеридного времени 0 января 1900 года.
В настоящее время вместо эфемеридного времени используют так называемое земное динамическое время, которое приблизительно соответствует эфемеридному.
Видео:Электронная таблица с расчётами горизонтальных солнечных часовСкачать

9.5. Атомное время
Развитие науки привело к ситуации, когда техническими средствами можно обеспечить измерение времени с большей точностью, чем из астрономических наблюдений. В 1964 г. Международный комитет мер и весов в качестве эталона времени принял атомные цезиевые часы.
В основе атомного времени лежит атомная секунда, как промежуток времени, за который происходит 9 192 631 771 колебание электромагнитной волны, которую излучает атом цезия при переходе с одного фиксированного энергетического уровня на другой.
Атомная секунда немного меньше эфемеридной, и за год разность между атомным и эфемеридным временем достигает 0.9 сек. Поэтому почти каждый год атомные часы переводят на 1 секунду назад. Сигналы точного времени, передаваемые по радио, соответствуют атомному времени. Эти сигналы передаются в виде шести секундных импульсов, причем начало последнего сигнала означает конец часа. Несколько радиостанций мира круглосуточно ведут непрерывную передачу сигналов точного времени.
Видео:Уравнение времени! Как использовать таблицу в наручных часах Arnold &Son Longitude II Trafalgar!Скачать

9.6. Системы счета времени
Местное время — это время, измеренное на данном географическом меридиане.
Разность любых местных времен на двух меридианах в один и тот же физический момент, равна разности долгот этих меридианов:
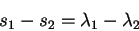 | (16) |
 | (17) |
 | (18) |
Всемирное время UT — местное среднее солнечное время гринвичского (

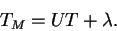 | (19) |
Поясное время. В 1884 г. введена поясная система счета среднего времени. Счет времени ведется только на 24 основных географических меридианах, расположенных друг от друга по долготе точно через 15 o начиная с нулевого меридиана. Границы поясов отстоят, как правило, на 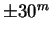
Декретное время. В 1930 г. декретом правительства СССР стрелки часов переведены на 1 час вперед относительно поясного времени:
Это время и называется декретным временем.
Летнее время. В 1981 г. в СССР, по примеру большинства стран мира, было введено еще и летнее время, на 1 час опережающее декретное. Летнее время вводится с последнего воскресенья марта по последнее воскресенье октября:
Таким образом, то время, которое мы называем московским, зимой является декретным временем второго часового пояса и опережает всемирное время UT на 3 часа. Летом отличие от гринвичского времени составляет 4 часа.
Видео:Математика это не ИсламСкачать

9.7. Связь среднего времени со звездным
Удобнее всего переходить от звездного времени к среднему через тропический год. Его продолжительность в звездных сутках ровно на одни сутки больше, чем продолжительность в средних солнечных сутках. Связано это с тем, что за год Солнце делает полный оборот на небесной сфере в ту же сторону, в какую вращается Земля. Поэтому за год Земля делает относительно Солнца на один оборот меньше, чем относительно звезд.
Тропический год равен 365.2422 средних солнечных суток и 366.2422 звездных суток. Поэтому связь среднего солнечного времени и звездного времени осуществляется через равенство: 365.2422 ср.суток = 366.2422 зв.суток. Или
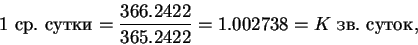 | (23) |
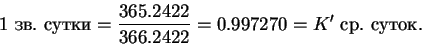 | (24) |
Все остальные единицы времени соотносятся друг с другом через эти же коэффициенты, т.е. 1 ср. час = 1.002738 зв. часа, и т.д., т.е.
Для удобства вычисления звездного времени на тот или иной момент, определенный по среднему солнечному времени, в Астрономическом Ежегоднике дается значение звездного времени на среднюю гринвичскую полночь S0. За средние солнечные сутки величина S0 увеличивается на 3 m 56 s .555, т.к. звездные сутки короче средних именно на эту величину.
Зная S0, можно вычислить звездное время s0в среднюю полночь на данном меридиане 
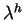
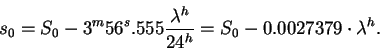 | (25) |
Для Казани ( 
Пример. Необходимо найти звездное время в Казани на момент 3 h среднего солнечного времени. Для этого надо найти звездное время в местную среднюю полночь s0, и прибавить к нему промежуток времени в средние 3 h , переведенный в промежуток звездного времени:
Видео:Астрономические способы измерения времени Владимир СурдинСкачать

9.8. Календарь
Календарь — это система счета длительных промежутков времени.
Природа предоставила нам 3 естественных периодических процесса: смена дня и ночи, смена лунных фаз, смена времен года. В разное время у разных народов в основе календаря лежали разные процессы, поэтому существовали солнечные, лунные, лунно-солнечные календари. В основе солнечных календарей лежит продолжительность тропического года, в основе лунных календарей — лунного месяца, лунно-солнечные календари сочетают оба периода.
Мы живем по солнечному календарю. Из практических соображений календарь должен удовлетворять следующим условиям:
1) Календарный год должен содержать целое число суток.
2) Продолжительность календарного года должна быть как можно ближе к продолжительности тропического года.
9.8.1. Юлианский календарь
Как мы уже знаем, тропический год содержит 365.2422 солнечных суток или 365 d 5 h 48 m 46 s 
Юлианский год длиннее тропического на 0 d .0078 и за 128 лет расхождение начинает составлять 1 сутки. Юлианским календарем пользовались около 16 столетий, и за это время накопилась разница в 10 суток. Это приводило к путанице в определении дат церковных праздников.
Например, по правилам христианской церкви праздник Пасхи должен наступать в первое воскресенье после первого полнолуния после дня весеннего равноденствия. В 325 г. день весеннего равноденствия приходился на 21 марта, а в 1582 г. — на 11 марта, что и приводило к трудностям в определении даты Пасхи.
9.8.2. Григорианский календарь
Реформа юлианского календаря стала необходимостью и в 1582 г. была проведена римским папой Григорием XIII, поэтому новый календарь носит название григорианского. Проект нового календаря был разработан итальянским математиком и врачом Лилио и направлен на приближение средней продолжительности календарного года к продолжительности тропического года. Суть реформы состоит в следующем.
1) Было устранено накопившееся расхождение в 10 суток юлианского календаря с счетом тропических лет (после 4 октября постановили считать 15 октября).
2) В юлианском календаре за 400 лет расхождение с реальным временем составляет почти ровно 3 суток. Поэтому в григорианском календаре принято не считать високосными те годы столетий, у которых номера не делятся без остатка на 400. Например, 2000 год был високосным, а 1900 — нет.
В результате средняя за 400 лет продолжительность календарного года в григорианском календаре составляет 365 d .2425, расхождение всего 0 d .0003, что даст расхождение в 1 сутки лишь через 3300 лет.
В России григорианский календарь был введен только в 1918 году (после 1 февраля постановили считать сразу 14 февраля), а православная церковь до сих пор пользуется юлианским.
Григорианский календарь называют еще новым стилем, а юлианский — старым стилем.
Начало календарного года (1 января), начало счета лет (от рождества Христова), деление года на 12 месяцев и недели по 7 дней — это условность, принятая по соглашению, традиция.
Видео:Время - Владимир Сурдин.Скачать

9.9. Линия перемены даты
При счете календарных дней необходимо условиться, на каком меридиане начинаются новые сутки. По международному соглашению таким меридианом является меридиан, отстоящий от гринвичского на 180 o . Линия перемены даты, в океане проходит по этому меридиану, и огибает острова. Так что линия перемены даты всюду проходит по акватории океана.
К западу от линии перемены даты, называемой еще демаркационной линией, число месяца всегда на единицу больше, чем к востоку от нее (например, к западу, на Чукотке, 15 сентября, а к востоку, на Аляске, 14 сентября), поэтому при пересечении демаркационной линии это небходимо учитывать. При пересечении этой линии с запада на восток надо уменьшить число месяца на единицу, а с востока на запад — прибавить. На морских судах такое изменение производят в ближайшую полночь после пересечения линии перемены даты. Суда, плывущие на восток, (из Китая в Калифорнию) дважды считают одну и ту же дату (после 15 сентября вновь наступает 15 сентября), а плывущие на запад (из Калифорнии в Китай) — пропускают одну дату (после 14 сентября сразу считают 16 сентября). Очевидно, что Новый год и новый месяц также начинаются на линии перемены даты.
Видео:Солнечный трекер. Слежение за Солнцем без фотодатчиковСкачать

9.10. Юлианские дни
В астрономии часто возникает задача определения числа суток, прошедших между двумя далеко отстоящими датами (наблюдения комет, переменных звезд, вспышки Новых и Сверхновых звезд).
Для удобства решения этой задачи в XVI веке н.э. Скалигер ввел понятие юлианского периода длиной 7980 лет, предложил считать за его начало 1 января 4713 года до н.э. и вести непрерывный счет дней, называемых юлианскими днями JD, начиная с этой даты. Началом юлианского дня считается средний гринвичский полдень. Юлианские даты дней текущего года даются в астрономических календарях и Астрономическом Ежегоднике. Например, 0 часов 1 января 2000 г. в Гринвиче это JD 2451544.5. Часто первые две цифры юлианской даты опускаются.
Период и дни названы Скалигером юлианскими в честь его отца Юлия, и не имеют отношения к Юлию Цезарю.
35. (269) Звезда 

Решение: Поправкой часов называется разность между правильным временем и показанием часов 

36. (228) В Орле по часам, идущим по киевскому звездному времени, в 4 h 48 m наблюдалась верхняя кульминация Капеллы ( 
Решение: Разность долгот двух пунктов равна разности двух любых местных времен, в данном случае звездных. В Орле звездное время равно прямому восхождению 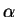

37. (233) Затмение Луны 2 апреля 1950 г. началось в 19 h 03 m по всемирному времени. Когда оно началось в Алма-Ате ( 
Решение: Поясное время равно всемирному плюс номер пояса в часах, так что Tп = 0 h 03 m 3 апреля. Декретное время опережает на 1 час поясное: Tд=1 h 03 m . Местное среднее солнечное время отличается от гринвичского на величину долготы в часах, поэтому TM = 0 h 11 m .
38. (263) Когда по поясному времени Казани ( 
Решение: В момент верхней кульминации Солнца истинное солнечное время 


39. (277) Пароход, покинув Владивосток в субботу 6 ноября, прибыл в Сан-Франциско в среду, 23 ноября. Сколько суток он был в пути?
Решение: Поскольку параход пересекал линию перемены даты с запада на восток, то на нем дважды считали одну и ту же дату, следовательно, число суток в пути было N d = 23 — 6 +1 = 18 d .
40. (270) В момент верхней кульминации 

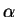

41. (232) Путешественники заметили, что по местному времени затмение Луны началось в 5 h 13 m , тогда как по астрономическому календарю это затмение должно было состояться в 3 h 51 m по гринвичскому времени. Какова их долгота?
42. (235) 14 июня по наблюдениям на судне, произведенным с секстаном, кульминация Солнца произошла в 8 h 23 m по хронометру, показывающему гринвичское звездное время. Кульминация произошла при зенитном расстоянии z=22 o 02′ (рефракция учтена). Определить долготу и широту судна, если по морскому астрономическому ежегоднику в этот день и час координаты Солнца были 
43. (267) Полное затмение Солнца должно было произойти в пункте с долготой 

44. (272) 26 сентября Солнце в пункте с долготой 
45. (278) Корабль, покинувший Сан-Франциско утром в среду 12 октября, прибыл во Владивосток ровно через 16 суток. Какого числа месяца и в какой день недели он прибыл?
Видео:Уравнение перевода местного солнечного времени в местное административное и наоборотСкачать

Уравнение времени
Калькулятор строит график уравнения времени (разницы между истинным солнечным и средним солнечным временем), также можно увидеть составные части уравнения времени, обусловленные эксцентриситетом и наклоном орбиты.
Этот калькулятор отображает уравнение времени, то есть разницу между истинным солнечным временем и средним солнечным временем на каждый день для заданной даты плюс указанное число лет. График отображает разницу в минутах. Кроме того отображаются отдельные компоненты уравнения времени. Если график выше нуля, то солнечные часы спешат, если ниже нуля — отстают от среднего солнечного времени.
Уравнение времени
Для отображения графика уравнения времени мы использовали приближенную формулу приведенную Рейнгольдом и Дершовицем в книге Календарные вычисления 1
Видео:Солнечные часыСкачать

Истинное солнечное время
Если при помощи точных часов измерить продолжительность солнечных суток, т.е. засечь разницу времени между двумя днями в момент когда солнце в зените (вертикальный предмет отбрасывает тень строго с севера на юг, или тени нет), мы обнаружим, что продолжительность солнечных суток отлична от 24 часов. В разные времена года эта продолжительность то увеличивается, то уменьшается. Отличие продолжительности солнечных суток от 24 часов может достигать 30 секунд. За несколько дней эти секунды разницы накапливаются и становятся заметны. В пределе разница времени на солнечных часах и обычных точных часах может достигать 16 минут. Таким образом истинное солнечное время, отображаемое солнечными часами идет неравномерно и пользоваться им для измерения равных промежутков времени с секундной точностью нельзя.
Видео:Солнечные часы - это не просто палка.Скачать

Причины неравномерности истинного солнечного времени
У Птолемея можно найти две основные причины, приводящие к неравномерности солнечного времени:
Истинными же (неодинаковой продолжительности) сутками мы называем время одного оборота 360 временных градусов равноденственного круга и еще некоторой дуги, конец которой восходит или проходит через меридиан одновременно с Солнцем в неравномерном его движении. Вот эта дополнительная сверх 360 градусов дуга равноденственного круга будет необходимо неодинаковой вследствие видимого неравенства движения Солнца, а также вследствие того, что равные отрезки круга, проходящего через середины зодиакальных созвездий, не в одинаковые времена проходят через горизонт или через меридиан. Правда, каждая из этих причин в течение одних суток производит незаметную разницу между средним и истинным временем оборота, но она становится очень заметной, если взять большее количество суток. 2
В этом тексте 2 века нашей эры видим, что уже древние астрономы, несмотря на ошибочную (геоцентрическую) модель движения планет, смогли правильно установить две причины, оказывающие влияние на неравномерность солнечных суток: наклон земной оси и неравномерность движения Солнца (читай Земли) относительно звезд.
Наклон земной оси
Во время солнцестояний солнце движется почти параллельно небесному экватору и его скорость перемещения практически полностью вычитается из суточного движения небесной сферы.Поэтому вблизи солнцестояний продолжительность солнечных суток максимальна. Во время равноденствий солнце движется под максимальным углом к небесному экватору и скорость его перемещения вычитается из суточного движения в наименьшей степени. Это укорачивает продолжительность солнечных суток. График синусоиды выражающей влияние наклона оси имеет период пол года и проходит в нулевой точке близко к периодам солнцестояний и равноденствий.
Эксцентриситет орбиты Земли
Земля движется вокруг Солнца по эллипсоидальной орбите в одном из фокусов которой находится Солнце. Согласно второму закону Кеплера, скорость движения Земли в ближайшей точке к Солнцу (перигелии) максимальна. В противоположной точке (афелии) — минимальна. Соответственно в перигелии солнечные сутки удлиняются больше всего, в афелии — укорачиваются. На графике составляющей эксцентриситета орбиты точки близкие к нулю соответствуют афелию и перигелию орбиты Земли. Период этого графика один год.
Видео:Солнечные часыСкачать

Среднее время, Историческая справка
Несмотря на невозможность прямого измерения, необходимость введения среднего времени возникла уже у античных астрономов.
Снова цитируем Птолемея:
На каждой из упомянутых частей зодиакального круга получается наибольшее прибавление или убавление: от солнечного неравенства — приблизительно З 2/3 градуса, а от разности времен при прохождении через меридиан — приблизительно 4 2/3 градуса. Таким образом, из вышеуказанного соединения на каждом из этих отрезков получается наибольшая разность с равномерным движением в 8 1/3 временных градусов, или 1/2 1/18 часть часа (т.е. 33 минуты), а между собой — вдвое больше, т.е. 16 2/3 временных градусов, или 1 1/9 час. Если мы пренебрежем такой величиной при наблюдении Солнца или других светил, то это, пожалуй, и не произведет заметного вреда при исследовании происходящих с ними явлений. Что же касается Луны, то вследствие быстроты ее движения это дает уже заметную разность, достигающую трех пятых одного градуса. 3
Таким образом среднее время понадобилось древним астрономам для измерения точного движения Луны по небесной сфере. Луна в свою очередь выступала ориентиром, для нахождения звезд в звездном каталоге, поэтому точность ее движения была крайне важна.
Среднее время удобно, в отличие от солнечного, оно течет равномерно. Измерить его с высокой точностью могут сейчас любые электронные или механические часы.
Уравнение времени
В древности точных часов не было, много веков приходилось довольствоваться солнечными часами, проблемы которых обозначены выше. Примитивные приборы античных времен были заменены математическими расчетами. Так появилось уравнение времени — то есть разница показаний солнечных часов и среднего времени, рассчитанная на каждый день года. Зная эту разницу древние астрономы могли привести показания солнечных часов к среднему времени, которое удобно для расчета движения других наблюдаемых на небосводе тел. В настоящее время больше распространены часы, отмеряющие среднее время и зная уравнение времени, мы можем вычислить показания солнечных часов.
Reingold, Edward M.; Dershowitz, Nachum. Calendrical Calculations. Cambridge University Press, 2018 стр. 215 ↩
Клавдий Птолемей, Альмагест Книга III, гл. 9 О неравенстве суток. Перевод И.Н. Веселовского, Москва, Наука, 1998. стр. 101 ↩
📸 Видео
Владимир Сурдин. ВремяСкачать

Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Работа солнечных часов и солнечный полденьСкачать

Время и календарьСкачать

Солнечное время. Короткометражный фильм.Скачать