В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.
За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.
- Угловое перемещение
- Угловая скорость и угловое ускорение
- Равномерное вращательное движение
- Равноускоренное вращательное движение
- Момент сил
- Примеры решения задач
- V011. Кинематика поступательного движения м т
- задачи
- Уравнение вращения твердого тела t t 2 4 . Определите частоту вращения, угловую скорость и ускорение через 10 с после начала движения.
- 📹 Видео
Видео:Вращательное движение. 10 класс.Скачать

Угловое перемещение
Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Угловая скорость и угловое ускорение
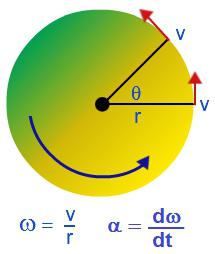
Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.
Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.
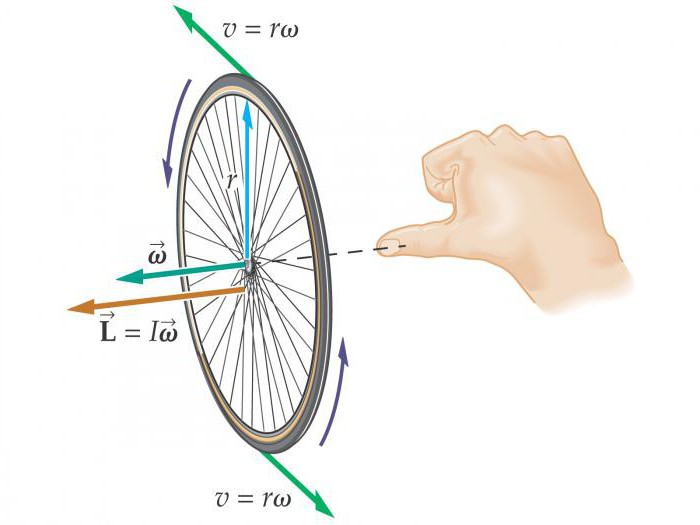
Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.
Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с 2 .
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.
Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Равномерное вращательное движение
Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ0 + ωt, где φ0 – начальное значение угла поворота.
Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Равноускоренное вращательное движение
Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω0+ εt, φ = φ0 + ω0t + εt 2 /2.
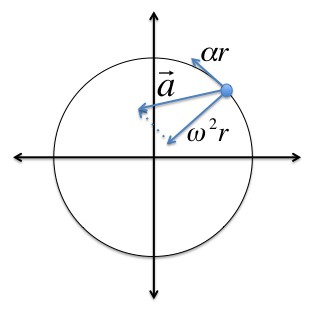
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑц = v 2 /R = (ωR) 2 /R = ω 2 R.
Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑt = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.
Видео:Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Момент сил
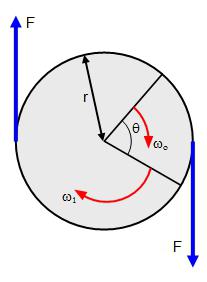
Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.
Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M1 + M2 + …+ Mn.
Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R 2 mβ, β= M/mR 2 = M/I, где I = mR 2 — момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Примеры решения задач
Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.
Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω0 — εt.
Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω0/t = 2πn/t.
Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).
Угол поворота ротора центрифуги за время t будет: φ(t)= φ0 + ω0t + εt 2 /2. Учитывая выражение для углового ускорения и то, что φ0 = 0, находим: φ(t)= ω0t/2 = πnt.
Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).
Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.
Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.
Найдем тормозной момент сил, действующий на диск: M = RF.
Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.
Найдем время, за которое диск остановится: t = ω0/ε, где ω0 — начальная угловая скорость диска, которая равна 2πv.
Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).
Ответ: время остановки равно 2,5 с.
Видео:Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

V011. Кинематика поступательного движения м т
| Название | V011. Кинематика поступательного движения м т |
| Дата | 18.06.2018 |
| Размер | 0.86 Mb. |
| Формат файла |  |
| Имя файла | Baza_NTK.docx |
| Тип | Документы #47211 |
| страница | 3 из 6 |
| Подборка по базе: 11111Викторины для школьников по правилам дорожного движения.doc, Роботтың динамикасы мен кинематикасы.docx, Порядок ограждения мест внезапно возникшего препятствия для движ, Алексеенко В.А., Копанев М.В., Целищев В.А._Синтез и анализ комб, Маршрут движения.docx, 6 Анализ движения денежных потоков.doc, ИДЗ Механика поступательного и вращательного движения.docx, 1.1 Кинематика точки.pdf, Теорема об изменении количества движения системы. Закон сохранен, полит партии и движения.docx Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать  задачи1. Вектор, равный по модулю углу поворота твердого тела и направленный вдоль оси вращения, называется … перемещением тела. 2. Направление вектора углового перемещения тела связано с направлением вращения тела правилом … буравчика. 3. При вращательном движении тела вокруг оси из векторов, являющихся кинематическими характеристиками движения, при любом характере вращения сонаправленными будут векторы 1) 2) 3) 4) все вектора направлены одинаково при любом движении 4. При вращательном движении тела вокруг оси, кинематическими характеристиками движения являются 1) 2) 3) 5.Вектор угловой скорости материальной точки определяется формулой 1) 6. Вектор углового ускорения материальной точки определяется формулой 1) 2) 3) 4) 7. Частица движется по окружности, ее угловая скорость меняется в соответствии с уравнением 8. Проекция угловой скорости тела на ось вращения зависит от времени согласно уравнению 9. Частица движется по окружности, в соответствии с уравнением 10. На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Уравнение, верно отражающее зависимость угловой скорости от времени, имеет вид 1) 3) 11. На графике представлена зависимость угловой скорости тела, вращающегося вокруг неподвижной оси, по окружности, от времени t. Уравнение, верно отражающее представленную зависимость, имеет вид 1) 4) 12. На графике представлена зависимость (парабола) угла поворота φ тела, вращающегося вокруг неподвижной оси, от времени t. Про характер движения рассматриваемого тела можно утверждать, что оно вращается 1) равноускоренно с начальной скоростью равной нулю 2) равноускоренно с отличной от нуля начальной скоростью 3) равнозамедленно с конечной скоростью равной нулю 13. На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. До остановки тело повернется на угол, равный … рад. (с округлением до десятых долей). 14. На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Модуль углового ускорения равен … рад/с 2 (с округлением до десятых долей). 15. Модуль угловой скорости точки, движущейся по окружности, изменяется с течением времени так, как показано на графике. Угол между векторами полного ускорения 1) увеличивается 2) уменьшается 3) не изменяется V 021. Законы Ньютона 1. Скорость тела не изменяется, если векторная сумма действующих на него сил равна нулю. Этот закон справедлив … 1 ) всегда 2) только в инерциальных системах отсчёта 3) только в системах отсчёта, неподвижных относительно Земли 4) только в системах отсчёта, неподвижных относительно Солнца 2. Падение тела на Землю рассматривается относительно трёх систем отсчёта. Телами отсчёта в этих системах являются а) планета Земля; б) автомобиль, движущийся равномерно и прямолинейно; в) самолёт, стартующий с аэродрома. Ускорение падающего тела будет одинаково в системах отсчета 1) а, б, в 2) а, б 3) а, в 4) б, в :2 3. При движении тел всегда совпадают по направлению два вектора 1) 4. .При переходе от одной ИСО к другой не изменяется численное значение величины 1) скорость 2) путь 3) перемещение 4) ускорение :4 5. На материальную точку действуют силы. Эта точка может: 1) двигаться с постоянной скоростью, если сумма всех действующих на неё сил не равна нулю 2) изменять направление своего движения относительно выбранной инерциальной системы отсчёта 3) двигаться с ускорением 4) покоиться относительно выбранной инерциальной системы отсчёта 6. На тело действуют две силы, обозначенные на рисунке векторами 1 и 3. Вектор ускорения тела совпадает с направлением вектора, обозначенного цифрой … 7. На покоящуюся точку начинают действовать четыре силы 1) в направлении силы 2) в направлении силы 3) в направлении силы 4) в направлении силы 5) остается в покое 8. На тело массы m действует сила 1) увеличится в 2 раза 2) увеличится в 4 раза 3) уменьшится в 2 раза 4) не изменится 9. На рис.1 показано направление вектора скорости v и ускорения a движущегося тела. Направление равнодействующей всех сил, действующих на тело, на рис.2 совпадает с направлением … :3 10. Величина равнодействующей двух равных по модулю сил F1 = F2 = 5,0 Н, направленных под углом 60 о друг к другу, равна … Н. 1) 5,0 2) 5 √3 3) 10 4) 7,0 :2 11. Тело, подвешенное на нити, совершает свободные колебания в вертикальной плоскости. Тангенциальное ускорение тела равно нулю, когда тело находится в положении … 12. . На рисунке изображен график зависимости проекции скорости Vх от времени для движущегося тела. Суммарная сила, действующая на это тело со стороны других тел, имеет максимальное значение на интервале времени 13. На рис.1 показаны вектора суммарной силы, действующей на тело, и скорости тела в некоторый момент времени. Направление ускорения этого тела совпадает с направлением вектора с номером … на рис 2. :1 14. Верное утверждение о направлениях скорости тела, его ускорения и суммарной силы, действующей на него, – 1) ускорение и сила всегда совпадают по направлению, а скорость может не совпадать 2) скорость, ускорение и сила всегда совпадают по направлению. 3) ускорение и сила всегда совпадают по направлению, а скорость направлена противоположно им 4) скорость и сила всегда совпадают по направлению, а ускорение направлено противоположно им 15. Тело массой m движется прямолинейно вдоль оси Ох. Движению тела под действием постоянной силы соответствует график номер … 16. Для сил, с которыми действуют друг на друга два взаимодействующих тела, справедливо утверждение 1) они равны по модулю и одинаково направлены 2) они равны по модулю и противоположно направлены 3) они различны по модулю и одинаково направлены 4) они различны по модулю и противоположны по направлению 17. На рисунке представлен график зависимости проекции ускорения аX от времени t для материальной точки, движущейся вдоль оси OX. На точку действовала постоянная сила, имеющая положительную проекцию на ось ОХ, на участке под номером 1) 1 2) 2 3) 3 4) 4 5) 5 18. Тело покоится на горизонтальной опоре. На рисунке показаны силы, действующие на тело и на опору. Третьим законом Ньютона связана пара сил 1) 19. Тело движется по гладкой горизонтальной поверхности. Пара сил, входящих в третий закон Ньютона, 1) 20. Тело находится в равновесии на наклонной плоскости. На рисунке показаны силы, действующие на тело и на опору. Третьим законом Ньютона связана пара сил 1) 4) ни одна из приведенных пар :2 21. Тело скользит с ускорением а вниз по наклонной плоскости с углом наклона к горизонту. Коэффициенту трения скольжения соответствует выражение 1) 22. Теннисный мяч летел с импульсом 1) вниз 2) вверх 3) вправо 4) влево :2 23. Два шара имеющие массы m1 и m2 действуют друг на друга с силами :2 2.На рисунке изображены графики зависимости силы F, действующей на материальную точку, от пройденного пути S. Сила F совершает одинаковую работу в случаях, приведенных под номерами 1) 1 и 2 3. На рисунке изображен график зависимости от времени работы, которую совершила над материальной точкой действующая на нее сила. Мощность этой силы обращалась в нуль в момент(ы) времени 1) 4. На рисунке изображен график зависимости от времени работы, которую совершила над материальной точкой действующая на нее сила. Кривая представляет собой параболу. Про модуль и знак мощности можно утверждать следующее: от 0 до 1) от 0 до 2) от 0 до 3) от 0 до 4) от 0 до 5) от 5. На рисунке указаны направления результирующей силы 6. На рисунке указаны направления результирующей силы 7. На рисунке изображены графики зависимости проекций сил на направление движения от пройденного пути. Максимальные значения 1) 1 и 3 2) 2 и 4 3) 2 и 3 4) 1 и 4 :2 8. На рисунке представлен график зависимости модуля силы 9. Материальная точка движется вдоль оси ОХ согласно уравнению 17. На рисунке изображен график зависимости от времениt. работы, которую совершила над материальной точкой действующая на нее сила. Верными являются утверждения: 1) мощность этой силы изменялась по модулю 2) мощность этой силы не изменялась по знаку 3) мощность этой силы обращалась в нуль на указанном интервале времени 4) траектория точки могла быть замкнутой за изображенный на рисунке промежуток времени 18. Тело движется по оси ОХ под действием силы, зависимость проекции которой от координаты х представлена на рисунке. Работа силы на пути 1) 19. Тело движется по оси ОХ под действием силы, зависимость проекции которой на ось ОХ от времениt представлена на рисунке. Мощность силы будет положительной и максимальной по модулю на интервале времени … 20. Две материальные точки aиb движутся вдоль оси Ох. На рисунке изображены графики зависимостей их координат от времени. Кинетическая энергия этих точек …… 1) для точки а — увеличивается 2) для точки а — не изменяется, 3) для точки а — уменьшается 4) для точки b – уменьшается 5) для точки b – увеличивается 6) для точки b — не изменяется 1.Для кинетической энергии НЕСПРАВЕДЛИВЫМ является утверждение 1) изменение кинетической энергии обусловлено работой консервативных и неконсервативных сил 2) кинетическая энергия зависит от скорости, с которой движется тело 3) кинетическая энергия является функцией координат 4) кинетическая энергия всегда положительна или равна нулю :3 2. Для кинетической энергии справедливыми являются утверждения: кинетическая энергия 1) является функцией механического состояния тела, т.е. ее приращение не зависит от пути (способа) перехода тела из одного состояния в другое, а определяется только механическими параметрами этих состояний 2) является величиной аддитивной, т.е. кинетическая энергия системы частиц равна сумме кинетических энергий этих частиц 3) является величиной инвариантной, т.е. сохраняется неизменным ее числовое значение при переходе от одной системы отсчета к другой 4) точки увеличивается, если над материальной точкой совершается положительная по знаку работа :1,2,4 3. Для потенциальной энергии справедливыми являются утверждения: 1) потенциальная энергия является функцией координат взаимодействующих тел (расстояния между ними) 2) модуль и знак потенциальной энергии зависят от выбора нулевого уровня потенциальной энергии, т.е. такого относительного расположения тел, при котором их потенциальную энергию полагают равной нулю 3) потенциальная энергия зависит (в классической механике) от выбора системы отсчета 4) убыль потенциальной энергии равна работе только консервативных сил, которые обусловливают эту энергию :1,2,4 4. Для потенциальной энергии НЕСПРАВЕДЛИВЫМ является утверждение 1) потенциальная энергия является функцией расстояния между взаимодействующими телами 2) потенциальная энергия не может быть отрицательной 3) убыль потенциальной энергии равна работе, совершаемой консервативными силами 4) численное значение потенциальной энергии не зависит от выбора системы отсчета. :2 5. Механическая система замкнута и неконсервативна. Верными являются утверждения: 1) векторная сумма всех внутренних сил, действующих в этой системе равна нулю 2) механическая энергия такой системы может возрастать 3) механическая энергия такой системы может убывать 4) механическая энергия такой системы может оставаться неизменной 5) векторная сумма всех внешних сил, действующих на эту систему равна нулю 6. Механическая система замкнута и консервативна. Верными являются утверждения: 1) векторная сумма всех внутренних сил, действующих в этой системе равна нулю 2) механическая энергия такой системы может возрастать 3) механическая энергия такой системы может убывать 4) механическая энергия такой системы остается неизменной 5) векторная сумма всех внешних сил, действующих на эту систему равна нулю 7. Тело массой m = 10 кг свободно падает с высоты Н =20 м с начальной скоростью V=0. Соотношение между кинетической Wкин и потенциальной энергией Wпот в точке на высоте h = 10 м от поверхности Земли 1) Wпот > Wкин 2) Wпот 20.На рисунке приведен график зависимости потенциальной энергии W n пружины от величины деформации х . Величина коэффициента упругости К пружины равна … 1) 210 5 Н/м 2) 410 5 Н/м 3) 1 10 5 Н/м 4) на основании рисунка коэффициент упругости пружины определить нельзя Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать  Уравнение вращения твердого тела t t 2 4 . Определите частоту вращения, угловую скорость и ускорение через 10 с после начала движения.
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение. ➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб. ➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам. ⚡ Условие + 37% решения: Уравнение вращения твердого тела t t 2 4 . Определите частоту вращения, угловую скорость и ускорение через 10 с после начала движения. Решение Согласно условию задачи, уравнение вращения твердого тела имеет вид: t t 2 4 Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени. Модуль угловой скорости равен: 4 8 1 / / 2 t t t с рад 810 1 81 Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени, либо второй производной от угла поворота тела по времени. Модуль углового ускорения равен: 8 1 8
Готовые задачи по физике которые сегодня купили: Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института 📹 ВидеоЛекция 06 Динамика твердого телаСкачать  Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать  Центростремительное ускорение. 9 класс.Скачать  Момент инерции абсолютно твердого тела. 10 класс.Скачать  Момент инерцииСкачать  Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать 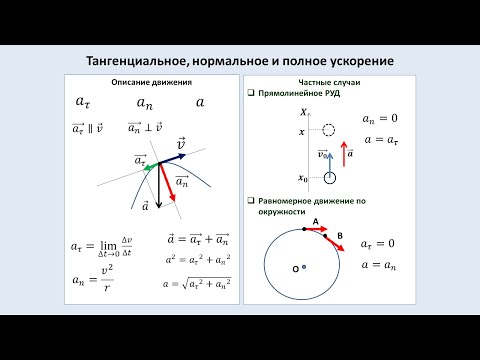 Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать  угловая и линейная скоростьСкачать  Кинематика твердого тела. Формула Эйлера. Формула Ривальса. Угловые скорости.Скачать  2.4. Угловая скорость и угловое ускорение твердого тела, вращающегося вокруг неподвижной оси, как векторы.Скачать  Физика - движение по окружностиСкачать  |
 ,
, 

 ,
,  2)
2)  3)
3)  4)
4) 
 . Время движения до остановки равно … сек.
. Время движения до остановки равно … сек. . Проекция углового ускорения при этом движении равна
. Проекция углового ускорения при этом движении равна , где φ – в радианах, t–в секундах. Проекция угловой скорости через 2 с после начала движения равна
, где φ – в радианах, t–в секундах. Проекция угловой скорости через 2 с после начала движения равна
 2)
2) 
 4)
4) 



 и мгновенной скорости
и мгновенной скорости  с течением времени
с течением времени
 2)
2)  3)
3)  4)
4)  :1
:1
 , которые изображены на рисунке. Под действием этих сил точка начинает двигаться …
, которые изображены на рисунке. Под действием этих сил точка начинает двигаться …




 . При увеличении модуля силы и массы тела в два раза ускорение точки
. При увеличении модуля силы и массы тела в два раза ускорение точки





 2)
2)  3)
3)  4) ни одна из приведенных пар :2
4) ни одна из приведенных пар :2 2)
2)  , 4)
, 4) 
 2)
2)  3)
3)  4) определенного ответа дать нельзя :3
4) определенного ответа дать нельзя :3 ( масштаб и направления указаны на рисунке). Теннисист произвел по мячу резкий удар с средней силой
( масштаб и направления указаны на рисунке). Теннисист произвел по мячу резкий удар с средней силой  . Изменившийся импульс мяча стал равным
. Изменившийся импульс мяча стал равным . Импульс силы, действующий на мяч, направлен…
. Импульс силы, действующий на мяч, направлен…
 и
и  . Правильно показаны эти силы на рисунке номер …
. Правильно показаны эти силы на рисунке номер …


 2)
2)  3)
3)  4) ни в один из перечисленных моментов :2
4) ни в один из перечисленных моментов :2 . Модуль силы
. Модуль силы  одинаков во всех случаях. Работа силы будет минимальной и положительной в случае … :4
одинаков во всех случаях. Работа силы будет минимальной и положительной в случае … :4

 на всех графиках одинаковы, пройденные пути – так же. Одна и та же работа соответствует графикам
на всех графиках одинаковы, пройденные пути – так же. Одна и та же работа соответствует графикам 
 от расстояния, пройденного телом при равномерном прямолинейном движении. Сила изменяется по закону
от расстояния, пройденного телом при равномерном прямолинейном движении. Сила изменяется по закону  , где a=const . Работа силы
, где a=const . Работа силы 
 , где С – положительная константа. Знак мощности Р силы, действующей на точку, определяется неравенством …
, где С – положительная константа. Знак мощности Р силы, действующей на точку, определяется неравенством …

 .
. представлена выражением
представлена выражением 
 2)
2)  3)
3)  4)
4)  :2
:2





