Видео:Вращательное движение. 10 класс.Скачать

Формула угловой скорости

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Определение и формула угловой скорости

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота $(varphi)$ . Часто используют вектор элементарного поворота $bar$ , который равен по величине элементарному углу поворота тела $(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой $omega$ . Математически определение угловой скорости записывают так:

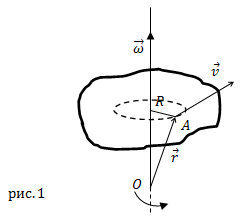
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($bar$ при этом изменяет направление).

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:

С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.

Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

Формула, связывающая линейную и угловую скорости

Линейная скорость $bar$ точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:

где $bar$ – перпендикулярная к оси вращения компонента радиус-вектора точки $A (bar)$ (рис.1). Вектор $bar$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.

Видео:Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с

В СГС: [$omega$]=рад/с

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Примеры решения задач

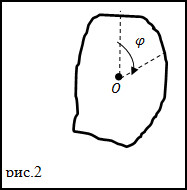
Задание. Движение тела с неподвижной осью задано уравнением $varphi=2 t-4 t^$, $(varphi)$ в рад, t в сек. Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении ( относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.

Решение. Для нахождения модуля угловой скорости применим формулу:

Используем заданную в условии задачи функцию $varphi(t)$, возьмем производную от нее по времени, получим функцию $omega(t)$:

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

Видео:угловая и линейная скоростьСкачать

Угловая скорость.

Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.

При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.

Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.

Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:

Угловая скорость выражается в радианах в секунду (рад/с).

При равномерном вращении, когда известна угловая скорость в начальный момент времени t₀ = 0, можно определить угол поворота тела за время t и тем самым положение точек тела:

За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:

Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:

А связь между линейной и угловой скоростями определяется соотношением:

Теоретическая механика:
Вращательное движение твердого тела

Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.

Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими a_t и a_n.

Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).

Закон вращательного движения тела выражается уравнением
φ = f (t).

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ_об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то
φ = 2πφ_об и φ_об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.

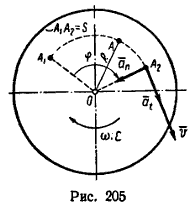
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a_t и a_n, характеризующими движение различных точек этого тела (рис 205).

Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой
a_t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
a_n = ω 2 R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.

Видео:Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

§ 33. Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид
φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,
φ = ωt.

Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.

Видео:Физика - движение по окружностиСкачать

§ 34. Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения
(1) φ = φ₀ + ω₀t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω₀ + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:
(4) φ = φ₀ + (ω 2 — ω₀ 2 )/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

Видео:Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

§ 35. Неравномерное вращательное движение

Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.

Видео:Скорость движения тела задана уравнениемСкачать

Уравнение вращения твёрдого тела описывается уравнением j = 3t2 + t.

Готовое решение: Заказ №8346

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 18.08.2020

Цена: 227 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Уравнение вращения твёрдого тела описывается уравнением j = 3t2 + t. Определите угловую скорость, угловое ускорение и частоту вращения тела через 10 с после начала движения.

Найдём зависимость угловой мгновенной скорости тела от времени: . Тогда зависимость частоты вращения тела от времени будет иметь вид: . Найдём зависимость углового мгновенного ускорения тела от времени:

• Тело массой 1 кг под действием постоянной силы движется прямолинейно по закону S = 2t2
• В некоторый момент времени угловая скорость вращения тела будет равна 12 с-1.
• Для спасения людей, блокированных в потерпевшем аварию автомобиле, необходимо вытащить шпильку
• Кусок металла, представляющий собой сплав меди и серебра, в воздухе имеет вес 2,5 Н

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🎬 Видео

Момент инерцииСкачать

Скорости и ускорения точек вращающегося телаСкачать

Поступательное и вращательное движенияСкачать

Кинематика вращательного движения. ТермехСкачать

Урок 96. Простейшие задачи на вращение твердого телаСкачать

Решение графических задач на равномерное движениеСкачать

Урок 88 (осн). Линейная скорость точки на вращающемся телеСкачать

Вращательное движение. ЗадачиСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать