Содержание

Уравнение вращения твердого тела имеет вид φ=3t2+t
Условие
Ответ
Решение
Теоретическая механика: Вращательное движение твердого тела
§ 33. Равномерное вращательное движение
§ 34. Равнопеременное вращательное движение
§ 35. Неравномерное вращательное движение
Уравнение вращения тела имеет вид фи t 3 4
💥 Видео

Видео:Вращательное движение. 10 класс.Скачать

Уравнение вращения твердого тела имеет вид φ=3t2+t

Реферат.Справочник
Решенные задачи по физике
Уравнение вращения твердого тела имеет вид φ=3t2+t

Условие

Уравнение вращения твердого тела имеет вид φ=3t2+t. Определить частоту вращения, угловую скорость и угловое ускорение твердого тела через 10 с после начала вращения. Дано: φ=3t2+t t=10 с Найти: ω,ε,ν-?

Ответ

ω=61 рад/с ε=6 рад/с2 ν=9,71 с-1

Решение

Угловая скорость вращения по определению: ω=dφdt=6t+1 Угловое ускорение по определению: ε=dωdt=6 Частота вращения: n=ω2π=6t+12π Подставив в формулы числовые значения, получим: ω=6t+1=61 рад/с ε=6 рад/с2 n=6t2π=9,71 с-1 Ответ: ω=61 рад/с ε=6 рад/с2 ν=9,71 с-1

Теоретическая механика:
Вращательное движение твердого тела

Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.

Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими a_t и a_n.

Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).

Закон вращательного движения тела выражается уравнением
φ = f (t).

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ_об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то
φ = 2πφ_об и φ_об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.

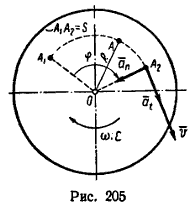
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a_t и a_n, характеризующими движение различных точек этого тела (рис 205).

Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой
a_t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
a_n = ω 2 R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

§ 33. Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид
φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,
φ = ωt.

Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

§ 34. Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения
(1) φ = φ₀ + ω₀t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω₀ + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:
(4) φ = φ₀ + (ω 2 — ω₀ 2 )/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

Видео:Лекция 06 Динамика твердого телаСкачать

§ 35. Неравномерное вращательное движение

Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.

Видео:Решение графических задач на равномерное движениеСкачать

Уравнение вращения тела имеет вид фи t 3 4

Угловое ускорение
ω = φ’ = A + 3Bt²
ω = 2+3*0,2*3² = 7,4 рад/с
Нормальное ускорение
an = ω²R
an = 7,4²*0,5 = 27,38 м/с²
Линейная скорость
v = ωR
Тангенциальное ускорение
aτ = v’=ω’R = 6Bt*R
aτ = 6*0,2*3*0,5 = 1,8 м/с²
Полное ускорение
a = √ (an² + aτ²)
a = √ (27,38² + 1,8²) ≈ 27,44 м/с²

Угловое ускорение
ω = φ’ = 2Bt + 3Ct²
ω = 2*(-1)*10 + 3*0,1*10² = -20+30 = 10 рад/с
Нормальное ускорение
an = ω²R
an = 10²*0,2 = 20 м/с²
Линейная скорость
v = ωR
Тангенциальное ускорение
aτ = v’=ω’R = (2B + 6Ct)R
aτ = (2*(-1)+6*0,1*10)*0,2 = (-2+6)*0,2=0,8 м/с²
Полное ускорение
a = √ (an² + aτ²)
a = √ (20² + 0,8²) ≈ 20,02 м/с²