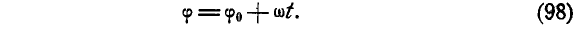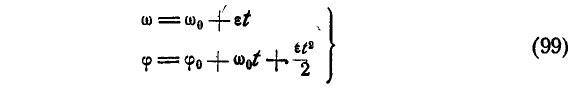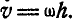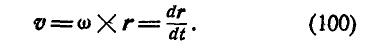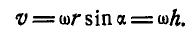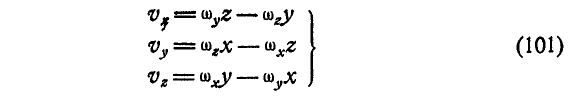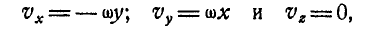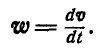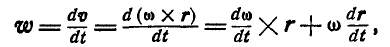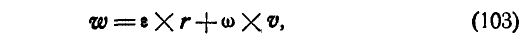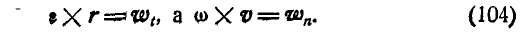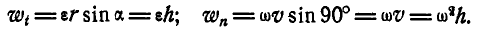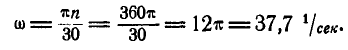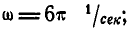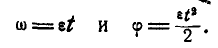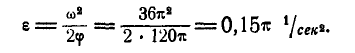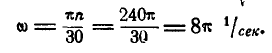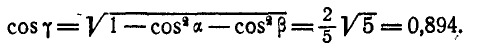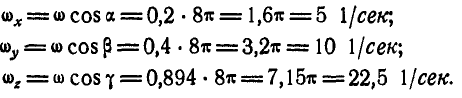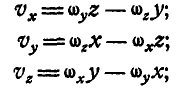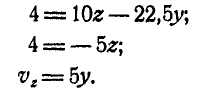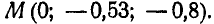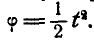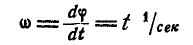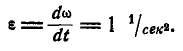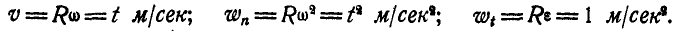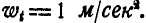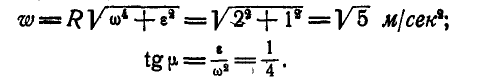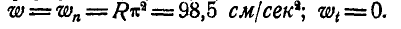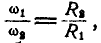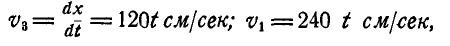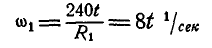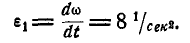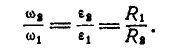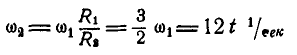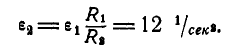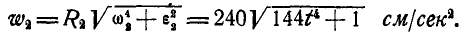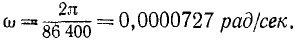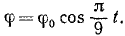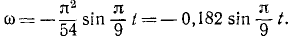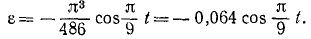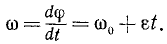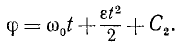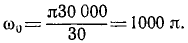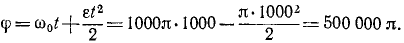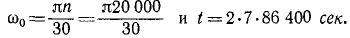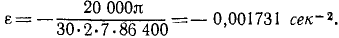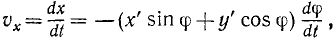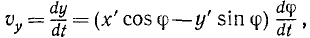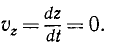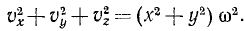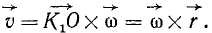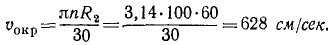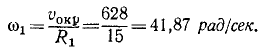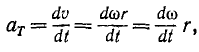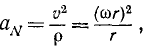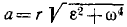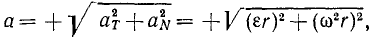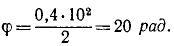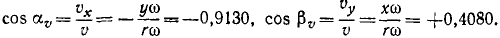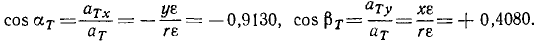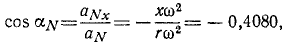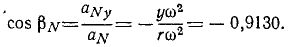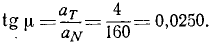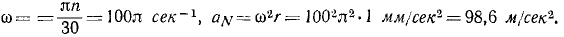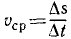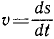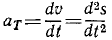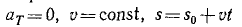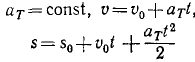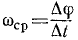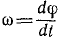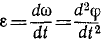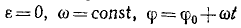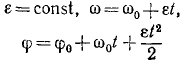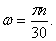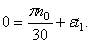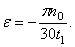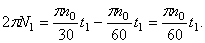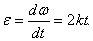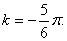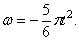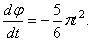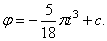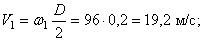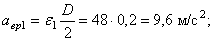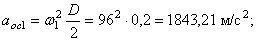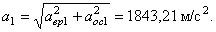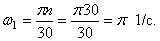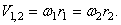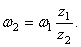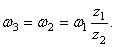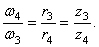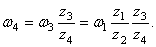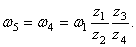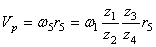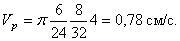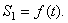Уравнение вращения диска вокруг неподвижной оси

Видео:Вращение тела вокруг неподвижной осиСкачать

Вращение твердого тела вокруг неподвижной оси в теоретической механике

Содержание:

Вращение твердого тела вокруг неподвижной оси:

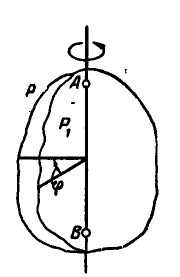
Вращением тела вокруг неподвижной оси называется такое его движение, при котором две точки тела, например А и В, неподвижны (рис. 162). Прямая, проходящая через указанные две неподвижные точки, называется осью вращения. Если мысленно провести через тело две полуплоскости — неподвижную

При вращении тела угол поворота его 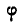изменяется с течением времени, а поэтому он является функцией времени:

Уравнение (97) называется уравнением вращения; зная его, можно для любого момента t найти угол 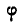, а следовательно, и положение вращающегося тела.

Величины угловой скорости и углового ускорения тела, вращающегося вокруг неподвижной оси, определяются по формулам (87) и (90).

Если 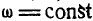, то такое вращение тела называется равномерным и уравнение вращения его (97) напишется аналогично уравнению (71) расстояний точки, движущейся равномерно:

Поэтому такое уравнение по аналогии с равномерным движением точки называется уравнением равномерного вращения.

Точно так же, если 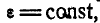то вращение тела называется равнопеременным.

Уравнения равнопеременного вращения тела могут быть выведены аналогично уравнениям (82) и (83) равнопеременного движения точки путем замены линейных характеристик угловыми и записаны в виде:

Условимся угловую скорость вращающегося тела изображать вектором, отложенным по оси вращения в такую сторону, чтобы, смотря с конца этого вектора, вращение тела происходило в направлении, противоположном движению часовой стрелки (рис. 163).

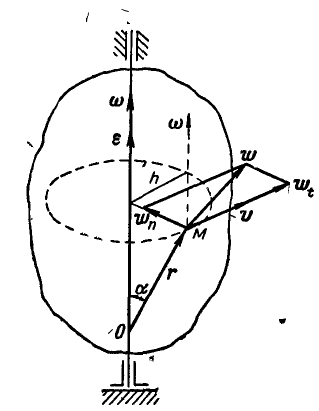
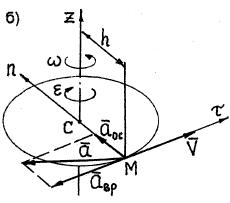
При вращении тела вокруг неподвижной оси (рис. 164) любая точка его М, отстоящая на расстоянии h от оси вращения, описывает окружность радиуса h и имеет линейную скорость, определяемую формулой (89):

Если провести из любой точки О оси радиус-вектор в точку М, то вектор линейной скорости точки М может быть представлен также в виде векторного произведения на :

В самом деле, раскрывая векторное произведение, получим величину скорости, определяемую формулой (89):

Вектор же скорости направлен перпендикулярно к плоскости векторов на в такую сторон, чтобы обход контура параллелограмма, построенного на на , задаваемый первым вектором , стоящим в векторном произведении, происходил против часовой стрелки, что согласуется с определением векторного, произведения двух векторов.

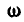
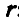
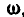
Рис. 164. Рис. 165.

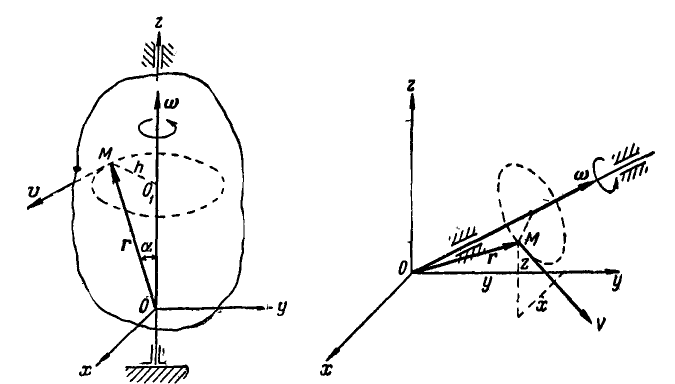
В самом общем случае, когда ось вращения тела составляет любые углы с координатными осями (рис. 165), проекции скорости точки М могут быть найдены по формулам проекций векторного произведения двух векторов (11):

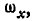
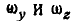
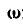
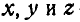
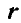
Равенства (101) называются формулами Эйлера. Здесь — проекции ; а —проекции на координатные оси.

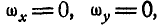
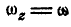
Если ось вращения вертикальна (рис. 164), то и формулы Эйлера принимают вид:

что было получено нами раньше (88). Мы уже знаем, что величина углового ускорения 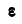определяется по формуле (90).

Введем в рассмотрение вектор углового ускорения е, под которым мы будем понимать векторную величину:

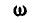
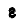
Так как имеет постоянное направление, то вектор всегда совпадает с осью вращения.

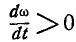
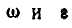
При векторы — одного направления;

при векторы — противоположных направлений.

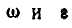
Нормальное и касательное ускорения любой точки М вращающегося тела (рис. 166) Moryт быть найдены по формулам (91):

Дадим векторное обобщение этим величинам. В самом общем случае вектор ускорения может быть найден по формуле (79):

Принимая во внимание формулы (100) и (102), имеем:

Действительно, в силу определения векторного произведения, находим:

Это приводит нас к формулам (91). Направления же 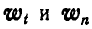соответствуют правилу откладывания векторов, полученных по правилам векторного произведения (рис. 166).

Задача №1

Маховик делает 360 об/мин. Найти его угловую скорость . ,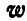

Решение. В нашем случае 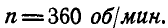По формуле (94) находим:

Задача №2

Маховик начинает вращаться равноускоренно из состояния покоя. Сделав с момента начала движения 60 оборотов, маховик имеет угловую скорость, равную 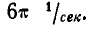Определить угловое ускорение маховика.

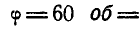
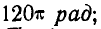
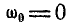
Решение. По условию задачи и

По формулам (99) получаем:

Подставляя значение 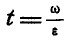, найденное из первого уравнения, во второе, находим:

Задача №3

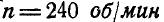
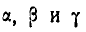
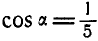
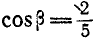
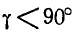
Тело делает вокруг оси, составляющей углы с координатными осями; при этом , и.

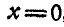
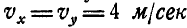
Найти такую точку тела, расположенную в плоскости , проекции скорости которой суть: .

Решение. Угловая скорость:

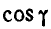
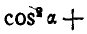
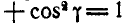
Для определения имеем известное соотношение: , откуда:

Найдем теперь проекции угловой скорости на координатные оси:

По формулам Эйлера (101) имеем:

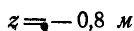
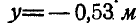
Из первых двух уравнений находим, что и , а поэтому искомая точка будет:

Задача №4

Маховик радиусом R = 1 м вращается вокруг неподвижной оси, проходящей через его центр перпендикулярно к плоскости чертежа, согласно уравнению

Найти скорость и ускорение точки М обода маховика по прошествии 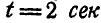после начала его движения. Для всех точек маховика, расположенных вдоль радиуса ОМ, изобразить графически скорости и ускорения.

Решение. Найдем сначала по формулам (87) и (90) угловую скорость и угловое ускорение маховика:

Далее, линейная скорость, нормальное и касательное ускорения’ точки М в момент t найдутся по формулам (89) и (91):

При 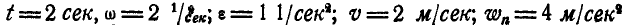и

Величина и направление ускорения точки М определятся по формулам (92) и (93):

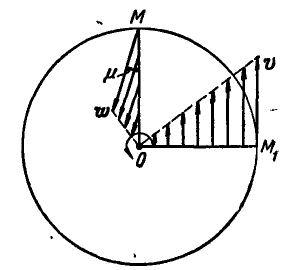
Так как величины линейных скоростей и ускорений точек, расположенных на одном из радиусов’маховика, например ОМ, зависят от величины самого радиуса, входящего в формулы (89) и (92) в первой степени, то отсюда следует, что концы векторов скоростей и ускорений точек одного радиуса будут расположены на прямой (рис. 167). Для удобства выполнения чертежа на радиусе ОМ дано изображение ускорений точек прямой ОМ, а на радиусе 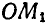— изображение скоростей.

Задача №5

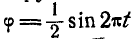
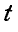
Диск, прикрепленный к вертикальной проволоке, совершает крутильные колебания вокруг оси проволоки так, что угол закручивания его меняется по закону: , где выражается в секундах.

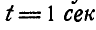
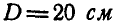
Найти нормальное, касательное и полное ускорения какой-либо точки М на ободе диска в момент , если диаметр диска (рис. 168).

Указание: находим сначала угловую скорость и угловое ускорение диска по формулам (87) и (90), а затем ускорение точки М по формулам (91) и (92).

Ответ.

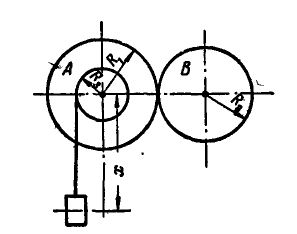
Рис. 169.

Задача №6

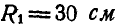
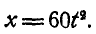
Зубчатое колесо А радиусом находится во внешнем зацеплении с колесом В радиусом (рис. 169). На выступ радиусом колеса А намотана нить, к концу которой подвешен груз. Движение груза в сантиметрах и секундах выражается уравнением: Найти угловую скорость и угловое ускорение колеса В, а также полное ускорение точки на ободе этого колеса.

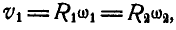
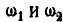
Решение. В общей точке касания колеса А и В имеют одинаковую линейную скорость, равную где — угловые скорости колес А и В. Отсюда следует, что

т. е. отношение угловых .скоростей колес обратно пропорционально их радиусам.

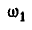
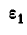
Найдем теперь угловую скорость , и угловое ускорение колеса А:

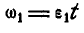
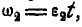
Вращение колес А и В равноускоренное, а поэтому и откуда

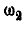
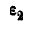
Отсюда угловая скорость и угловое ускорение колеса В:

Ускорение какой-либо точки обода колеса В находим по формуле (92):

Видео:Вращательное движение. 10 класс.Скачать

Вращение твердого тела вокруг неподвижной оси

Вращением вокруг неподвижной оси называют движение твердого тела, при котором его точки описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к их плоскостям

Вращательное движение

Как было показано, для определения движения твердого тела достаточно определить движение трех его точек, не лежащих на одной прямой. Пусть во- время движения тела две его точки О и O₁ остаются неподвижными.

Тогда движение тела можно определить движением третьей точки К, принадлежащей телу и не лежащей на одной прямой с точками О и O₁. Выберем эту точку произвольно и, соединив все три точки прямолинейными отрезками, получим треугольник OO₁K-Так как точки О и O₁ неподвижны, то неподвижна и сторона OO₁ треугольника OO₁K, и движение точки К, а также и всего тела определится поворотом плоскости треугольника OO₁K вокруг прямой OO₁. Точку К мы выбрали произвольно, следовательно, поворачивается вокруг прямой OO1 любая плоскость, проведенная в теле через эту прямую. Такое движение тела называют вращательным движением, или, коротко, вращением, а неподвижную прямую OO₁, вокруг которой вращается тело, называют осью вращения.

Ось вращения может проходить и за пределами тела. Так, например, Луна, двигаясь вокруг Земли, повернута к ней всегда одной стороной. Движение Луны по отношению к Земле можно назвать вращением. Ось вращения проходит за пределами Луны через центры круговых траекторий ее точек.

Если движение тела определять по движению его точек, то вращение вокруг оси можно определить как движение твердого тела, при котором все точки тела описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к плоскостям этих окружностей, а ось вращения можно определить как неподвижную прямую, на которой расположены центры окружностей, описываемых точками вращающегося тела.

Вращательное движение твердого тела определено, если задан как функция времени угол, на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела: φ=φ(t)

Уравнение вращательного движения. Построим основную систему координат xcyz, направив ось Oz по оси вращения тела (рис. 101). Эта система неподвижная и не связана с вращающимся телом. Построим теперь другую, подвижную, систему координат x’0y’z’, направив ось Oz’ также по оси OO₁ вращения тела, а ось Ox’ — на какую-либо точку K₁ тела. Эта система координат неизменно связана с телом и поворачивается вместе с ним относительно основной системы xOyz. Угол φ на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела, называют углом поворота и обозначают буквой φ. Так, если в начальное мгновение оси Ox’ и Ox (см. рис. 101) совпадали, то углом поворота мы назовем двугранный угол между неподвижной плоскостью xθz и подвижной плоскостью x’Oz’ или равный ему линейный угол x’Ox’.

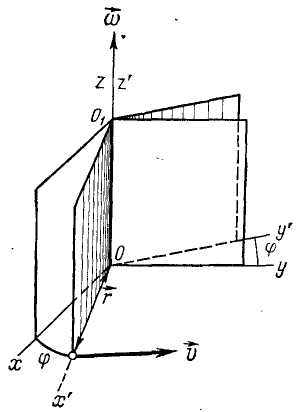
Рис. 101

Угол φ можно рассматривать как угловую координату тела, потому что он определяет положение всего вращающегося тела. Измеряется угол φ в радианах.

Будем считать угол φ положительным, если он отсчитан от положительной оси Ox к положительной оси Оу, т. е. против вращения часовой стрелки, если смотреть с положительного направления оси Oz. При отсчете в противоположную сторону будем считать угол отрицательном.

Чтобы определить вращение тела, надо знать угол поворота как некоторую непрерывную однозначную функцию времени:

Уравнение (82) является уравнением вращательного движения твердого тела вокруг неподвижной оси.
Всякая плоскость OO₁K, проведенная через ось вращения и какую-либо точку К тела, поворачивается за данное время на такой же угол φ, на который за это же время повернулась плоскость x’Oz’. Это следует из условия неизменяемости твердого тела.

Угловая скорость выражается первой производной от угла поворота по времени:

Угловая скорость. Угол поворота характеризует вращение тела только с геометрической стороны. Чтобы охарактеризовать вращение тела не только в пространстве, но и во времени, возьмем отношение изменения ∆φ угла поворота ко времени Δt, в течение которого это изменение происходило, называемое средней угловой скоростью тела:

(83′)

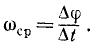
Пределом отношения (83′) при Δt, стремящимся к нулю, является первая производная от угла поворота по времени. Она характеризует изменение угла поворота в данное мгновение, т. е. характеризует вращение тела не только по отношению к окружающему пространству, но и во времени. Эта величина принята за пространственно-временную меру вращения твердого тела вокруг оси и ее называют угловой скоростью тела:

(83)

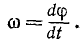
Знак производной (83) указывает, в какую сторону поворачивается тело вокруг оси Oz: если производная (83) положительна, то наблюдатель, смотрящий с положительной стороны оси Oz, видит тело вращающимся против часовой стрелки, т. е. справа налево — от положительного направления оси Ox к положительному направлению оси Оу: при отрицательной производной (83) вращение тела происходит в обратном направлении.

Размерность угловой скорости равна размерности угла поворота, деленной на размерность времени. Но угол поворота является отвлеченной величиной, и размерность его—единица. Следовательно, размерность угловой скорости обратна размерности времени.

Чаще всего время измеряют в секундах, тогда единица угловой скорости ceκ -1 .

Равномерное вращение иногда характеризуют числом п оборотов, совершаемых телом за единицу времени (обычно за минуту).

Найдем соотношение между угловой скоростью ω, выраженной в радианах в секунду, и числом оборотов в минуту. Если тело делает n оборотов в минуту, то оно поворачивается за каждую минуту на 2πn радианов, а за секунду—в 60 раз меньше, следовательно,

(84)

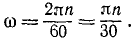
Формулу (84) широко применяют в технической механике. Приближенно можно считать

(84′)

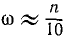
В формулах (84) и (84′) n выражеyо в оборотах за минуту, a ω — в радианах за секунду, как их большей частью и выражают. Однако для очень медленно вращающихся тел число оборотов удобнее считать не за минуту, а за другие единицы времени. Так, Земля вращается вокруг своей оси, делая 1 оборот в сутки. Было бы неудобно считать, что Земля делает 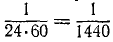оборота в минуту. Угловую скорость Земли следует подсчитывать не по формуле (84), а из тех соображений, что Земля делает один оборот (2π радианов) за сутки, а в сутках 86400 сек, следовательно,

Самые медленные вращения встречаются в звездном мире. Так -2 .

Чаще всего время измеряется в секундах, тогда единица углового ускорения ceκ -2 , или по записи, рекомендованной ГОСТом, pa∂/ceκ 2 .

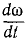
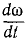
Если с течением времени абсолютная величина угловой скорости тела увеличивается, то производная имеет тот же знак, что и ω, и вращение тела ускоренное. Если же величина угловой скорости с течением времени уменьшается, то производная и угловая скорость имеют различные знаки — вращение тела замедленное. Каждое из этих вращений, и ускоренное и замедленное, называют переменным вращением.

Задача №7

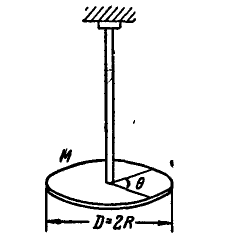
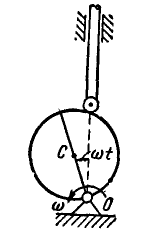
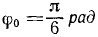
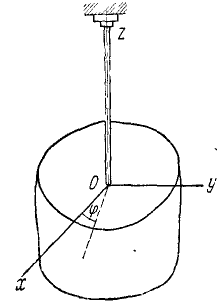
Унифиляр (тело, подвешенное на вертикальном стержне) (рис. 102) закрутили на угол от равновесного положения и затем (в мгновение t = 0) предоставили самому себе, и он стал вращаться согласно уравнению

Рис. 102

Определить угловую скорость (в ρa∂/ceκ.) и угловое ускорение (в рад/сек) через каждые 3 сек от начала движения.

Решение. Дифференцируя уравнение движения, получим выражение угловой скорости унифиляра:

Дифференцируя вторично найдем, угловое ускорение унифиляра:

Чтобы определить угол поворота, угловую скорость и угловое ускорение в заданные мгновения, надо в уравнение движения тела и в полученные соотношения подставить t = 3, 6, 9, . и т. д. секунд. Анализируя полученные данные относительно ω и ε, убедимся, что унифиляр совершает крутильные колебания с периодом 18 сек.

Равномерное и равнопеременное вращения

Если угловая скорость ω постоянна, то производная 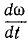= 0, и вращение равномерное. Таким образом, при равномерном вращении тела угловое ускорение равно нулю, угловая скорость постоянна, а угол поворота изменяется пропорционально времени:

ε = 0, ω = const, φ = φ₀+ωt, (86)

где φ₀-начальное значение угла.

Формулы (86) справедливы только для равномерного вращения тела и неприменимы при других движениях.

Из различных переменных вращений тела в задачах наиболее часто встречается равнопеременное вращение. Равнопеременным вращением называют такое вращение твердого тела вокруг оси, πph котором угловое ускорение остается постоянным:

Интегрируя это уравнение, находим

Постоянную интегрирования C₁ находим из начальных данных. В начальное мгновение (при t=0) величина угловой скорости была ω₀. Подставляя эти частные значения аргумента t и функции ω, находим постоянную C₁:

Интегрируя это равенство, получаем

Постоянную C₂ находим из начальных данных. Если при начале вращения тело было повернуто на некоторый угол φ₀, то, подставляя φ₀ вместо φ и 0 вместо t, найдем C₂ = φ₀. Для равнопеременного вращения тела имеем:
(87)

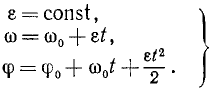
Формулы (87) справедливы только для равнопеременного вращения твердого тела и неприменимы при других движениях.

Задача №8

Барабан суперцентрифуги делает при установившемся движении 30000 об/мин, а после прекращения подачи энергии (на выбеге) вращается равнозамедленно с угловым ускорением ε=π1∕ceκ 2 . Определить время выбега (время до остановки) и угол поворота барабана за это время.

Решение. В мгновение прекращения подачи энергии угловая скорость барабана была

C этого мгновения барабан вращается равнозамедленно по (87):

В мгновение остановки барабана угловая скорость его равна нулю. Подставляя это значение угловой скорости, находим время выбега.

t = 1000 сек = 16 мин 40 сек.

За это время барабан повернется на угол

Чтобы по углу поворота определить число оборотов, надо поделить этот угол (выраженный в радианах) yа 2π—число радианов в одном обороте.

Ответ. t = 16 мин 40 сек, φ = 250 000 об.

Задача №9

В инерционном аккумуляторе Уфимцева (1918 г.) для ветроэлектрических станций стальной диск вращается в глубоком вакууме, делая 20 000 об/мин. Предоставленный самому себе, он продолжает вращаться в течение двух недель. Определить е диска, считая вращение равнозамедленным.

Решение. Определим начальную угловую скорость диска н время (2 нед.) до остановки в секундах:

Ответ получим, разделив ω₀ на t.

Ответ.

Траектории, скорости и ускорения точек вращающегося тела

Точки вращающегося тела, расположенные на одной прямой, параллельной оси вращения, совершают одинаковые движения

Траектории точек вращающегося тела

Вращением тела называют движение, при котором точки тела описывают окружности с центром на оси вращения. Следовательно, по самому определению вращательного движения траектории точек тела—окружности.

Если тело мысленно пересечь какой-либо плоскостью, перпендикулярной оси вращения, то в этой плоскости будут находиться круговые траектории всех расположенных в ней точек тела. Очевидно, что движения точек тела, лежащих на ном в какой-либо из точек к этой плоскости, совершенно одинаковы, а потому и движение точек всего тела может быть полностью охарактеризовано движением точек, лежащих в этой плоскости.

Сохраним и в этом параграфе расположение осей координат (см. рис. 101), при котором оси Oz и Oz’ неподвижной и подвижной систем совпадают с осью вращения тела, а плоскость x’0y’ находится в плоскости хОу.

Возьмем в этом теле какую-либо точку К (рис. 103), координаты которой относительно подвижной системы обозначимx’,y’ и г’. Эти координаты точки К во время вращения тела не меняются, так как оси подвижной системы координат неизменно связаны с телом и вращаются вместе с ним. Координаты той же точки в основной системе обозначим х, у и z.

Координаты х и у точки К связаны с координатами х’ и у’ той же точки формулами, известными из аналитической геометрии и понятными из чертежа (рис. 103):

х = х’ cos φ—y’ sin φ, (88′)

y = x’ sin φ +y’ os φ. (88″)

Если тело вращается, то с течением времени меняется угол φ, являющийся некоторой функцией (71) от времени t, а следовательно, меняются и координаты х и у точки К в основной системе отсчета. Координата же z при направлении оси Oz вдоль оси вращения не изменяется и остается равной z’:

Аналогично можно определить подвижные координаты по неподвижным и углу φ:

х’ = х cos φ у sin φ; y’ = y cos φ—x sinφ; z’ = z.

Скорость точки тела, вращающегося вокруг оси, равна произведению угловой скорости тела на расстояние точки от оси: υ= ωr

Скорости точек вращающегося тела. Для получения проекций скорости на неподвижные оси координат продифференцируем по времени равенства (88), рассматривая φ как функцию времени. Будем иметь

Но согласно (88) выражение, стоящее в скобках в первом из этих равенств, есть у, а во втором х, а потому 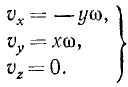(89)

Возводя эти равенства в квадрат и складывая, найдем

Но в левой части мы имеем квадрат полной скорости точки, а в скобках правой части — квадрат расстояния точки от оси. Мы получили одну из главнейших формул кинематики:
υ = ωr (90)

— величина скорости точки вращающегося тела равна произведению угловой скорости тела на расстояние точки от оси вращения.

Таким образом, для определения скорости точки вращающегося тела нет необходимости знать ее координаты, надо знать лишь расстояние точки от оси вращения и угловую скорость тела.

Можно определить угловую скорость тела по скорости какой-либо из его точек и по расстоянию этой точки от оси вращения:

(91)

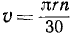
По этим формулам можно определить скорость любой точки вращающегося тела, независимо от того, какую форму имеет тело и находится точка на поверхности или внутри тела. Скорость точки тела, вращающегося вокруг оси, называют вращательной скоростью точки. Она направлена перпендикулярно к плоскости, проходящей через точку и ось вращения, против хода часовой стрелки или по ходу часовой стрелки в зависимости от знака производной (83).

Если же смотреть на тело с той стороны оси вращения, куда мы направили вектор 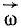угловой скорости, то вектор вращательной скорости всякой точки тела направлен против хода часов. Такое же направление (против хода часов) имеет вектор , если смотреть на него с конца вектора вращательной скорости .

Следовательно, вектор вращательной скорости точки и по величине и по направлению можно рассматривать как момент вектора угловой скорости тела относительно этой точки. Его можно представить в виде векторного произведения аналогично тому, как это сделано в статике с моментом силы относительно точки.

Вращательную скорость точек, лежащих на поверхности цилиндра (шкива, барабана, махового колеса, вала и т. п.), вращающегося вокруг своей оси, называют окружной скоростью тела. Окружная скорость равна произведению ω на радиус R тела:

Задача №10

Определить вращательную скорость точек земной поверхности на экваторе и на широте Москвы (55°45′) при вращении Земли вокруг оси (рис. 104). Средний радиус Земли 6371 км и cos 55 o 45′ = 0,5628.

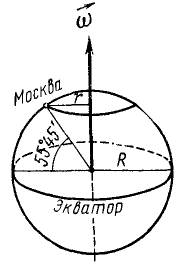
Рис. 104

Решение. Вращаясь вокруг своей оси, Земля совершает один оборот (2π рад) за сутки (86 400 сек), и угловая скорость Земли ω=727∙10 -7 pa∂/ceκ. Умножая угловую скорость на радиус Земли, выраженный в метрах (6371 ∙ 10 3 ), найдем вращательную скорость точек Земли на экваторе:

υ= ωR=727 • 6371 • 10 -4 = 463 м/сек.

Для определения вращательной скорости точек в Москве надо умножить ω Земли на расстояние г от Москвы до земной оси:

υ = 727 • 10 -7 • 0,5628 • 6371 • 10 3 = 261 м/сек.

Ответ. Вращательная скорость точек на экваторе 463 м/сек, в Москве 261 м/сек.

Она направлена против вращения часовой стрелки, если смотреть с северного полюса.

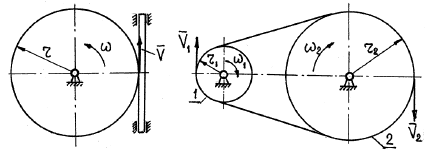
Задача №11

Шкив динамомашины R₁= 15 см (рис. 105) вращается посредством бесконечного ремня от паровой машины со шкивом R₂ — 60 см, делающим 100 об/мин. Определить угловую скорость ω₁ шкива динамомашины.

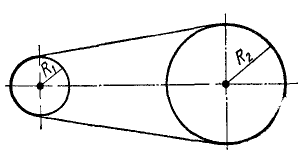
Рис. 105

Решение. Определим окружную скорость шкива паровой машины:

Такова же величина скорости частиц ремня, а следовательно, и окружная скорость шкива динамомашины. Его угловая скорость

Ответ. ω₁=41,87 рад/сек, n = 400 об/мин.

Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения тела: α_r=e_r

Ускорение точек вращающегося тела

Если в выражении касательного (69) и нормального (74) ускорений вместо скорости v мы подставим выражение (90) вращательной скорости, то получим касательное и нормальное ускорения точки тела, вращающегося вокруг неподвижной оси.

Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения.

Центростремительное ускорение точки вращающегося тела равно произведению квадрата угловой скорости тела на расстояние точки от оси вращения тела:
αN=ω 2 r

Каждая точка вращающегося тела описывает окружность, а потому радиус кривизны р траектории точки равен расстоянию этой точки от оси вращения тела. Имеем

Нормальное ускорение точки вращающегося тела обычно называют центростремительным ускорением. Оно равно произведению квадрата угловой скорости на расстояние точки от оси вращения тела.

Величина полного ускорения точки тела, вращающегося вокруг оси, выражается формулой

Зная касательное и центростремительное ускорения, определим по формуле (75) величину полного ускорения этой точки:

. (94)

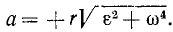
Иногда бывает необходимо определить проекции ускорения точки вращающегося тела на неподвижные оси координат. Для этого продифференцируем равенства (89) по времени, учитывая, что при вращении тела меняется не только его угловая скорость, но и координаты х и у его точек:

Подставляя вместо υ_x и υ_y их значения (89), найдем проекции ускорения точки вращающегося тела на неподвижные оси:

. (95)

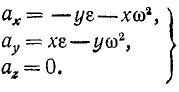
Возводя в квадрат и складывая, найдем

a 2 = (x 2 + y 2 ) (ε 2 + ω 4 ),

или, так как x 2 +y 2 = r 2 , получаем уже знакомую нам формулу (94). Следовательно,

Задача №12

Тело вращается вокруг оси Oz без начальной угловой скорости и с постоянным угловым ускорением ε = 0,4 рад/сек 2 . Определить для t = 10 сек: 1) координаты точки К тела, если при t = 0 координаты точки К были: х = +10, y=0, z-0∙, 2) ее вращательную скорость; 3) направляющие косинусы вращательной скорости; 4) касательное и центростремительное ускорения той же точки; 5) направляющие косинусы касательного и центростремительного ускорений; 6) угол, составляемый векторами полного и центростремительного ускорений.

Решение. Тело вращается равноускоренно; по (87) найдем угловое ускорение, угловую скорость и угол поборота тела для заданного мгновения: ε = 0,4 ρaд/ceκ 2 ; ω = 0,4 • 10 = 4 ρaд/ceκ;

Тело повернулось за 10 сек на 20 рад. Переведем радианы в градусы:

за вычетом полных оборотов определим угол αr, составляемый радиусом-вектором с осью Ox (рис. 106):

20 рад = 65 о 54’56»,

По тригонометрическим таблицам находим: cos a_r = 0,4080, sin a_r = 0,9130. Приняв во внимание, что расстояние точки К от оси вращения тела равно 10 см, найдем координаты точки К в мгновение t=10 сек:

х=10 cos a_r = +4,080 см,

y = 10 sin a_r = +9,130 см.

Величину вращательной скорости определим по (90):

υ = ωr = 4 • 10 = 40 см/ceκ.

Чтобы определить направляющие косинусы вращательной скорости, найдем сначала по (89) ее проекции на оси координат:
υ_x= — yω = — 36,52 см/сек,

по затем по (62) — направляющие косинусы:

Определим по (92) величину касательного ускорения:

и по (95′) — проекции касательного ускорения на оси х и у:

a_Tx = — yε=—3,652 см/сек 2 , a_Ty = xε =+1,632 см/сек 2 .

Разделив проекции на модуль касательного ускорения, найдем направляющие косинусы касательного ускорения:

Мы видим, что направляющие косинусы касательного ускорения тождественны с направляющими косинусами скорости.

Напомним, что знак направляющего косинуса определяется знаком числителя. Если ω и ε имеют одинаковые знаки (как в данной задаче), то тело вращается ускоренно и направление касательных ускорений его точек совпадает с направлением их скоростей, если же знаки ω и ε различны, то вращение замедленное и векторы касательных ускорений и скоростей точек направлены в противоположные стороны.

Величину центростремительного ускорения определим по (93);

a_N=ω 2 r = 4 2 ∙10 = 160 см/сек 2

и по (95′) —его проекции на оси координат:

a_Nx=—xω 2 = —65,280 см/сек 2 ,

a_Ny = — yω 2 = —146,080 см/сек 2 .

Проекции нормального ускорения точки на оси координат имеют знаки, обратные знаку соответствующей координаты точки. В самом деле, ayx отрицательна, если абсцисса х положительна, и положительна, если х отрицательна (аналогично и ayy). Следовательно, центростремительное ускорение всегда направлено к началу координат, т. е. к центру круговой траектории точки.

Разделив проекции центростремительного ускорения на его модуль, найдем направляющие косинусы центростремительного ускорения:

Так как касательное ускорение перпендикулярно к центростремительному, то (по условию перпендикулярности, известному из аналитической геометрии) сумма произведений соответствующих направляющих косинусов должна равняться нулю. Действительно,

cos a_T cos a_N + cos β_T cos β_N = ( — 0,9130) ( —0,4080) + ( + 0,4080) ( — 0,9130) =0.

Определим теперь тангенс угла между направлением полного и нормального ускорений:

Пользуясь таблицами тригонометрических функций, определим, что угол равен l o 26’0″.

Ответ. 1) х = + 4,080 см, у = + 9,130 см; 2) υ = 40 см/сек, 3)cos a_υ=—0,9130, cos β_υ = +0.4080; 4) a_T = 4 см/сек1, a_N= 160 см/сек 2 ; 5) cos a_T=—0,9130, cos β_T= +0,4080, cos a_N = — 0,4080, cos β_N=—0,9130; 6) угол равен l o 26’0″.

Задача №13

При сборке ротора молотковой дробилки была допущена неточность, в результате которой центр тяжести ротора отстоит от оси вращения на расстоянии 1 мм. Определить центростремительное ускорение центра тяжести ротора, если n = 3000 об/мин.

Решение. По формулам (84) и (93) имеем

Ответ. a_N=98,6 м/сек 2 ≈ 10g.

Зависимости между углом поворота, угловой скоростью, угловым ускорением и временем аналогичны зависимостям между расстоянием, скоростью, касательным ускорением и временем

Аналогия формул

Формулы кинематики вращательного движения аналогичны соответствующим формулам кинематики точки и могут быть из них получены, если заменить расстояние s углом поворота φ, скорость υ— угловой скоростью ω и касательное ускорение α_T-угловым ускорением ε. Это правило является мнемоническим, оно непригодно для вывода формул, но может облегчить их запоминание. Ниже приведен ряд формул, получающихся одна из другой такой заменой.

Уравнение движения по траектории
s=s(t)

Средняя скорость точки

Величина скорости точки

Величина касательного ускорения

Равномерное движение точки

Равнопеременное движение

Уравнение вращения вокруг оси
φ=φ(t)

Средняя угловая скорость тела

Величина угловой скорости тела

Величина углового ускорения

Равномерное вращение тела

Равнопеременное вращение

• Сферическое движение твердого тела
• Плоско-параллельное движение твердого тела
• Движение твердого тела, имеющего неподвижную точку
• Движение твердого тела
• Теория пар, не лежащих в одной плоскости
• Произвольная пространственная система сил
• Центр параллельных сил и центр тяжести
• Поступательное движение твердого тела

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Вращение твердого тела

Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δ φ , угловое ускорение ε и угловая скорость ω :

ω = ∆ φ ∆ t , ( ∆ t → 0 ) , ε = ∆ φ ∆ t , ( ∆ t → 0 ) .

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

Рисунок 1. Вращение диска относительно оси, проходящей через его центр O .

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

в котором r – модуль радиус-вектора r → .

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Векторы v → и a → = a τ → направлены по касательной к окружности радиуса r .

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

a n = v 2 r = ω 2 r .

Если разделить вращающееся тело на небольшие фрагменты Δ m i , обозначить расстояние до оси вращения через r i , а модули линейных скоростей через v i , то запись формулы кинестетической энергии вращающегося тела будет иметь вид:

E k = ∑ i ν m v i 2 2 = ∑ i ∆ m ( r i ω ) 2 2 = ω 2 2 ∑ i ∆ m i r i 2 .

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

I = ∑ i ∆ m i r i 2 .

В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в С И – килограмм—метр в квадрате ( к г · м 2 ) . Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела m v 2 2 , вместо массы m в формулу входит момент инерции I . Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω .

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

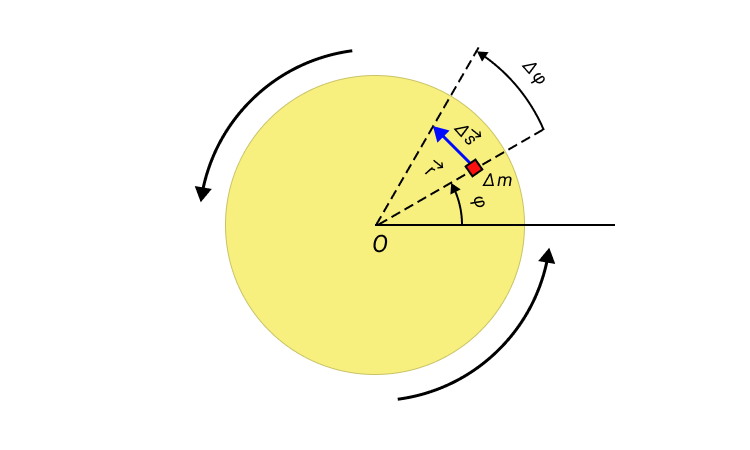
Положение x C , y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2 , расположенными в плоскости X Y в точках с координатами x 1 , y 1 и x 2 , y 2 определяется выражениями:

x C = m 1 x 1 + m 2 x 2 m 1 + m 2 , y C = m 1 y 1 + m 2 y 2 m 1 + m 2 .

Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

r C → = m 1 r 1 → + m 2 r 2 → m 1 + m 2 .

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

r C → = ∑ m i r i → ∑ m i .

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

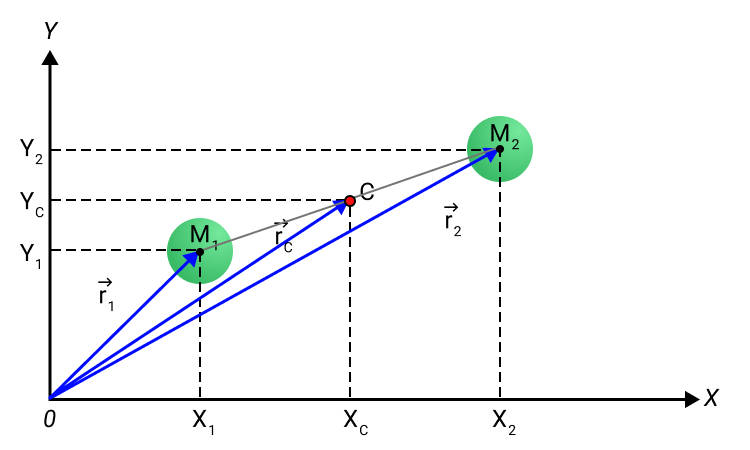
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

Рисунок 3. Определение положения центра масс C тела сложной формы. A 1 , A 2 , A 3 точки подвеса.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

E k = m v C 2 2 + I C ω 2 2 ,

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

Рисунок 4. Качение колеса как сумма поступательного движения со скоростью v C → и вращения с угловой скоростью ω = v C R относительно оси O , проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Видео:Вращение твердого тела вокруг неподвижной оси. Момент инерции. Примеры. Лекция 7-1Скачать

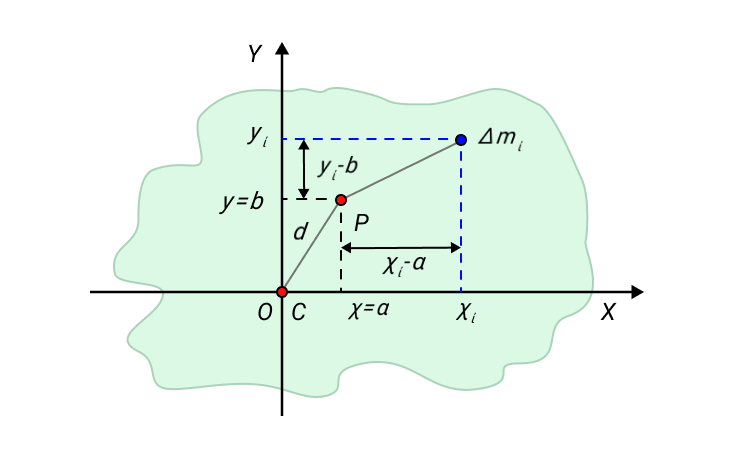
Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С . Выберем систему координат Х У с началом координат 0 . Совместим центр масс и начало координат.

Одна из осей проходит через центр масс С . Вторая ось пересекает произвольно выбранную точку Р , которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δ m i .

По определению момента инерции:

I C = ∑ ∆ m i ( x i 2 + y i 2 ) , I P = ∑ m i ( x i — a ) 2 + y i — b 2

Выражение для I P можно переписать в виде:

I P = ∑ ∆ m i ( x i 2 + y i 2 ) + ∑ ∆ m i ( a 2 + b 2 ) — 2 a ∑ ∆ m i x i — 2 b ∑ ∆ m i y i .

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

I P = I C + m d 2 ,

где m – полная масса тела.

Рисунок 7. Модель момента инерции.

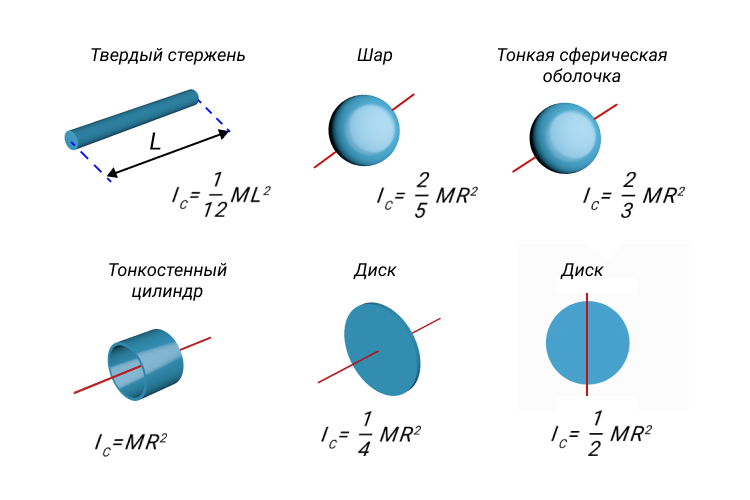
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Видео:§2.2. Вращение твердого тела вокруг неподвижной оси.Скачать

Основное уравнение динамики вращательного движения твердого тела

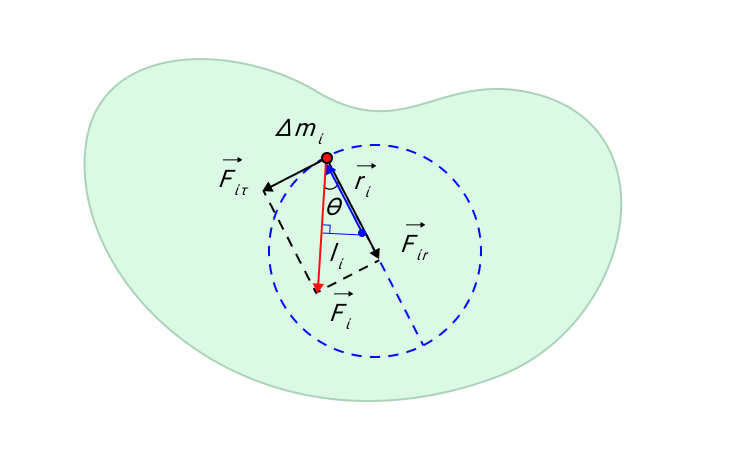
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О . Ось вращения расположена перпендикулярно плоскости рисунка.

Δ m i – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть F i → . Ее можно разложить на две составляющие: касательную составляющую F i τ → и радиальную F i r → . Радиальная составляющая F i r → создает центростремительное ускорение a n .

Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

Касательная составляющая F i τ → вызывает тангенциальное ускорение a i τ → массы Δ m i . Второй закон Ньютона, записанный в скалярной форме, дает

∆ m i a i τ = F i τ sin θ или ∆ m i r i ε = F i sin θ ,

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r i , то мы получим:

∆ m i r i 2 ε = F i r i sin θ = F i l i = M i .

Здесь l i – плечо силы, F i , → M i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

∑ ∆ m i r i 2 ε = ∑ M i .

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

∑ M = ∑ M i в н е ш н + ∑ M i в н у т р .

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M . Так мы получили основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω → , ε → , M → определяются как векторы, направленные по оси вращения.

Видео:Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной осиСкачать

Закон сохранения момента импульса

В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p → . По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Для обозначения момента импульса используется латинская буква L .

Поскольку ε = ∆ ω ∆ t ; ∆ t → 0 , уравнение вращательного движения можно представить в виде:

M = I ε = I ∆ ω ∆ t или M ∆ t = I ∆ ω = ∆ L .

M = ∆ L ∆ t ; ( ∆ t → 0 ) .

Мы получили это уравнение для случая, когда I = c o n s t . Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется: ∆ L = 0 , если M = 0 .

L = l ω = c o n s t .

Так мы пришли к закону сохранения момента импульса.

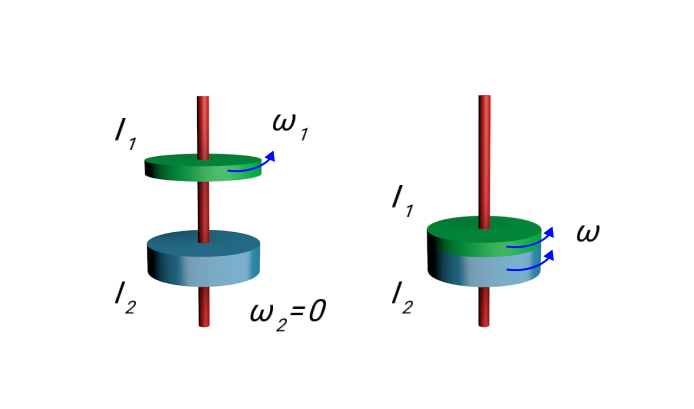
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1 ω 1 = ( I 1 + I 2 ) ω .

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

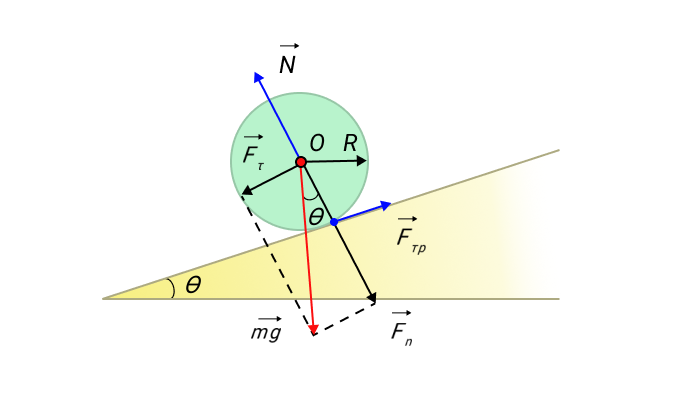
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Ось вращения O проходит через центр масс тела. Моменты силы тяжести m g → и силы реакции N → относительно оси O равны нулю. Момент M создает только сила трения: M = F т р R .

Уравнение вращательного движения:

I C ε = I C a R = M = F т р R ,

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O , проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

m a = m g sin α — F т р .

Исключая из этих уравнений F т р , получим окончательно:

α = m g sin θ I C R 2 + m .

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара I C = 2 5 m R 2 , а у сплошного однородного цилиндра I C = 1 2 m R 2 . Следовательно, шар будет скатываться быстрее цилиндра.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Уравнение вращения диска вокруг неподвижной оси

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

Кинематика вращения тела вокруг неподвижной оси

1. Краткие сведения из теории

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид

. (40)

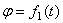
Отсчет угла ведется от выбранного начала. При этом углам, отложенным в направлении движения часовой стрелки, придается знак “минус”, а углам противоположного направления – знак “плюс”.

Угол поворота выражается в радианах. Иногда угол поворота определяется числом оборотов N. Зависимость между и N следующая .

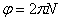
Угловая скорость тела:

(41)

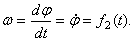
Знак производной 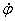дает возможность установить происходит ли вращение тела в положительном направлении отсчета угла поворота (знак “плюс”) или в обратную сторону (знак “минус”). Единица измерения угловой скорости – радиан в секунду (или 1/с).

Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой n . Зависимость между и n имеет вид

Угловое ускорение тела:

(42)

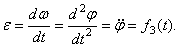
Знак производной 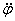дает возможность установить является ли вращение тела в данный момент времени ускоренным или замедленным. Если знаки и одинаковы, тело вращается ускоренно, а если их знаки различны – замедленно. Единица измерения углового ускорения – радиан на секунду в квадрате (или 1/с 2 ).

Траекториями точек тела, не лежащих на оси вращения, являются окружности с центрами на оси вращения и радиусами, равными кратчайшему расстоянию от этих точек до оси вращения.

Модуль скорости любой точки тела, находящейся на расстоянии h от оси вращения (рис. 18), определяется по формуле

. (43)

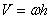
Направлена скорость точки по касательной к описываемой точкой окружности в сторону движения.

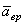
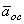
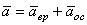
Ускорение любой точки тела состоит из двух составляющих – вращательного и осестремительного ускорений:

.

Модуль вращательного ускорения точки определяется по формуле

. (44)

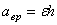
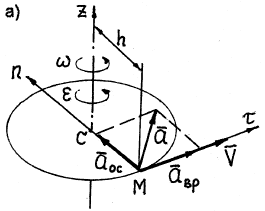
Вращательное ускорение направлено по касательной к описываемой точкой окружности в ту же сторону, что и его скорость, если вращение тела ускоренное (рис. 18, а) и в сторону, противоположную скорости, если вращение замедленное (рис.18, б).

Модуль осестремительного ускорения определяется по формуле

. (45)

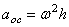
Осестремительное ускорение всегда направлено по радиусу окружности от точки к центру окружности (рис. 18).

Модуль полного ускорения точки определяется по формуле

(46)

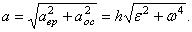
2. Основные типы задач кинематики вращения тела вокруг оси

В зависимости от того, что задано в условии задачи и что требуется определить, различают следующие два основных типа задач.

1. Исследуется движение тела в целом. В этих задачах вначале нужно получить законы (40)–(42) и, используя связь между ними, определить требуемую величину (см. примеры 17 и 18).

2. Требуется определить скорости и ускорения отдельных точек тела. Для решения задач этого типа вначале надо установить кинематические характеристики движения всего тела в целом, т.е. найти , и . После чего по формулам (43), (44), (45), (46) определить скорости и ускорения точек тела (см. пример 19).

Пример 17. Пропеллер самолета, делающий 1200 об / мин , после выключения двигателя останавливается через 8 с. Сколько оборотов сделал пропеллер за это время, если считать его вращение равнозамедленным?

Вначале получим законы вращения пропеллера (40), (41) и (42). По условию задачи пропеллер вращается равнозамедленно , из этого следует, что

.

, (47)

(48)

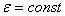
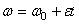
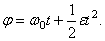
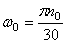
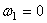
Начальной угловой скоростью при замедленном вращении будет та, которую пропеллер имел до выключения двигателя. Следовательно, . В момент остановки при t₁ = 8 сек. угловая скорость тела . Подставляя эти значения в уравнение (47), получим

Отсюда

Если обозначить число сделанных пропеллером за время t₁ оборотов через N₁, то угол поворота за то же время будет равен

.

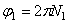
Подставляя найденные значения и в уравнение (48), получим

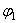
Отсюда 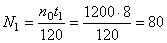оборотов.

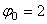
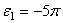
Пример 18. Найти закон вращения тела вокруг оси, если известны следующие данные: угловая скорость изменяется пропорционально t 2 , начальный угол поворота рад, для заданного момента времени t₁ = 3 с угловое ускорение 1/с 2 .

По условию задачи модуль угловой скорости изменяется пропорционально t 2 . Обозначая неизвестный коэффициент пропорциональности буквой k , имеем

. (49)

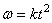
Найдем , беря производные по времени от обеих частей равенства (49),

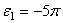
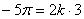
Определим коэффициент k из условия, что при t₁ = 3 сек. угловое ускорение 1/с 2 : или

Подставляя значение k в уравнение (49), получим

Учитывая, что 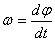, будем иметь

Умножая обе части этого уравнения на dt и интегрируя, находим

В начальный момент при t = 0, 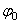= 2 рад, следовательно, c = 2.

Таким образом, 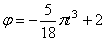радиан.

Пример 19. В период разгона ротор электродвигателя вращается по закону 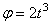, где t в сек, в рад.

Определить в конце 4-й секунды линейную скорость, вращательное, осестремительное и полное ускорения точки, лежащей на ободе ротора, если диаметр ротора D = 40 см .

По заданному уравнению вращения ротора находим его угловую скорость и угловое ускорение , .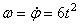

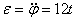
Подставляя значение t₁ = 4 сек в выражение для и , найдем

1/с,

1/с 2 .

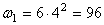
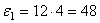
Определим модули линейной скорости, вращательного и осестремительного ускорений в этот же момент времени по формулам (43), (44) и (45)

Модуль полного ускорения точки обода ротора определим по формуле (46)

3. Определение скоростей и ускорений в случаях, когда вращающееся тело входит в состав различных механизмов

Рассмотрим механизмы с поступательным и вращательным движением звеньев. Решение задачи начинают с определения скоростей точек того звена, для которого движение задано. Затем рассматривают звено, которое присоединено к первому звену и т.д. В результате определяют скорости точек всех звеньев механизма. В такой же последовательности определяют и ускорения точек.

Передача вращения от одного вращающегося тела, называемого ведущим, к другому, называемому ведомым, может осуществляться при помощи фрикционной или зубчатой передачи (рис. 19).

Во фрикционной передаче вращение передается вследствие действия силы трения в месте контакта соприкасающихся колес, в зубчатой передаче – от зацепления зубьев. Оси вращения ведущего и ведомого колес могут быть параллельными (рис. 19, а, б) или пересекаться (рис. 19, в). В рассмотренных случаях линейные скорости точек А соприкасания колес одинаковы, их модули определяются так:

. (50)

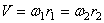
Отсюда 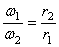. (51)

То есть угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

При преобразовании вращательного движения в поступательное (или наоборот) часто используют зацепление зубчатого колеса с зубчатой рейкой (рис. 20). Для этой передачи выполняется условие: .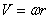

Кроме фрикционной и зубчатой передач, существует передача вращения при помощи гибкой связи (ремня, троса, цепи) (рис. 21).

Так как модули скоростей всех точек ремня одинаковы и ремень не скользит по поверхностям шкивов, то соотношения (50) и (51) относятся и к ременной передаче.

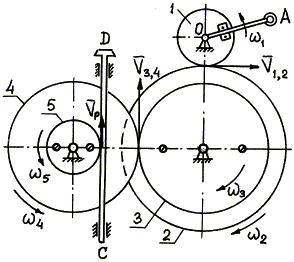
Пример 20. В механизме домкрата при вращении рукоятки ОА шестерни 1, 2, 3, 4, 5 приводят в движение зубчатую рейку ВС домкрата (рис. 22).

Определить скорость рейки, если рукоятка ОА делает 30 оборотов в минуту ( n = 30 об /мин). Числа зубцов шестерен: z₁ = 6, z₂ = 24, z₃ = 8, z₄ = 32; радиус пятой шестерни r₅ = 4 см .

Так как рукоятка ОА жестко соединена с шестерней 1, то последняя делает тоже 30 об /мин или

Модули скоростей точек соприкасания зубчатых колес 1 и 2 одинаковы для точек обоих колес и определяются по формуле (50)

Отсюда 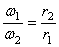(см. также (51)).

Так как числа зубьев пропорциональны радиусам колес, то .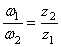

Отсюда

Шестерни 2 и 3 жестко соединены между собой, поэтому

Для находящихся в зацеплении колес 3 и 4 на основании (51) можно записать

Отсюда

Шестерни 4 и 5 жестко соединены между собой, поэтому

Модули скоростей точек соприкосновения зубчатой рейки ВС и шестерни 5 одинаковы, поэтому

или

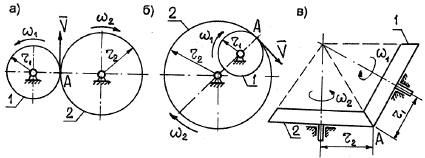
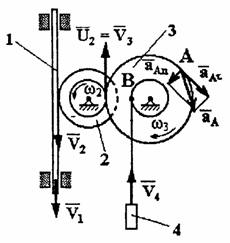
Пример 21. Рейка 1, ступенчатое колесо 2 с радиусами R ₂ и r ₂ и колесо 3 радиуса R ₃ , скрепленное с валом радиуса r₃, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис.23). Рейка движется по закону

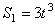
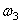
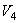
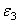
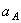
Дано: R ₂ =6 см, r₂=4 см, R₃=8 см, r₃=3 см, ( S — в сантиметрах, t — в секундах), А — точка обода колеса 3, t ₁ =3 с. Определить: , , , в момент времени t = t₁.

Указания. Пример 21 — на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы, при этом считается, что ремень по ободу колес не скользит.

Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса R ₁ ), через V₁, а точек, лежащих на внутренних ободах (радиуса r ₁ ), через U₁.

1. Зная закон движения рейки 1, находим ее скорость:

. ( 52 )

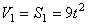
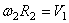
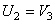
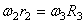
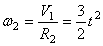
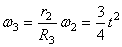
Так как рейка и колесо 2 находятся в зацеплении, то V ₂ = V₁ или . Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, или . Из этих равенств находим:

, . (53)

Тогда для момента времени t₁ = 3 сек. получим 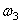= 6,75 с -1 .

2. Определяем V ₄ . Так как 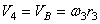, то при t₁=3 c ек . V ₄ = 20 ,25 см/с.

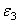
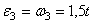
3. Определяем . Учитывая второе из равенств (53), получим .

Тогда при t₁ = 3 сек. 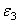= 4,5 с -2 .

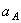
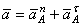
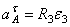
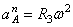
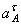
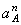
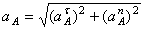
4. Определяем . Для точки А , где численно , . Тогда для момента времени t₁ = 3 сек. имеем = 36 см/с2, = 364,5 см/с2.

= 366,3 см/с 2 ,

Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис.2.

Ответ: 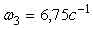, см/ с , , .

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

🔍 Видео

Семинар 6. Вращение твердых тел вокруг неподвижной осиСкачать

Лекция 06 Динамика твердого телаСкачать

Вращательное движение твердого тела вокруг неподвижной осиСкачать

Диск вращается вокруг вертикальной оси: Волькенштейн 2.100Скачать

Момент инерцииСкачать

Поступательное и вращательное движенияСкачать

Кинематика вращательного движения. ТермехСкачать

Т.К. 2 темы: вращательное движение твёрдого тела вокруг неподвижной оси; преобразование движенийСкачать

Урок 94. Вычисление моментов инерции телСкачать

Урок 96. Простейшие задачи на вращение твердого телаСкачать

Момент инерции абсолютно твердого тела. 10 класс.Скачать