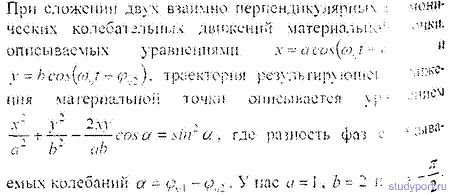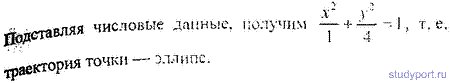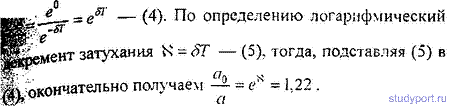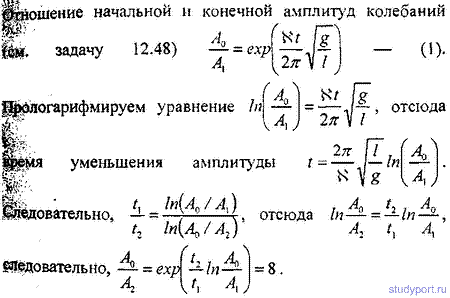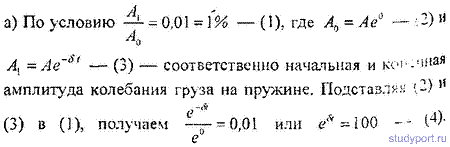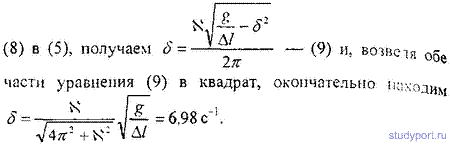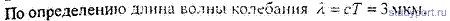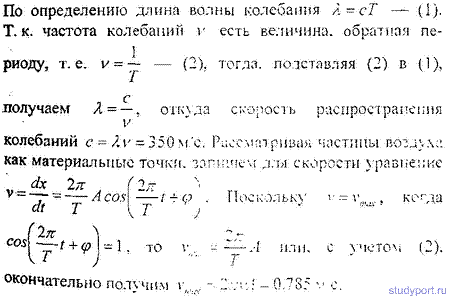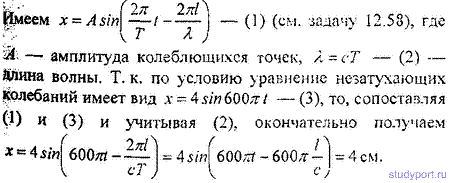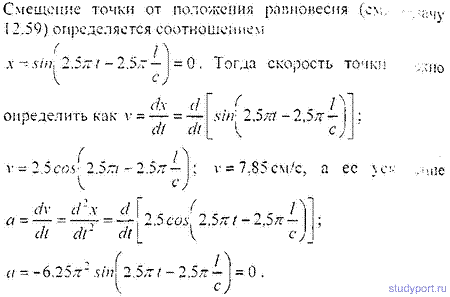Уравнение волны в момент времени t 4 после начала колебаний (4 видео)

Примеры решения расчетных задач

Ход занятия

Для выполнения задания необходимо вспомнить основные характеристики волны и записать в тетради: амплитуда волны, фаза волны. Также следует вывести уравнение стоячей волны, чтобы убедиться в том, что стоячая волна образуется в результате интерференции бегущей и отраженной волны.

Качественные задачи

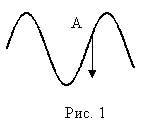
1. В бегущей волне частица А имеет направление скорости, указанное на рис. 1. В каком направлении «движется» волна?

2. Почему не могут быть поперечными упругие волны в газе?

3. При образовании волн частицы воды не перемещаются вдоль направления их распространения, а лишь участвуют в колебательном движении около некоторого среднего положения. Почему же морское волнение часто выбрасывает на берег различные плавающие в море предметы?

4. Может ли существовать в природе плоская гармоническая волна, или это физическая идеализация, лишь приближенно описывающая реальность?

5. Могут ли космонавты при выходе в открытый космос общаться между собой при помощи звуковой речи?

6. В воду погружен вибратор, мембрана которого издает музыкальные звуки. Будет ли находящийся под водой пловец воспринимать мелодию такой же, какой он слышал бы ее в воздухе?

7. Перед игрой инструменты «настраивают». В чем физическая сущность настройки скрипки, мандолины и других струнных инструментов?

Примеры решения расчетных задач

Задача 1. Плоская волна с периодом Т = 1,2 с и амплитудой колебаний a = 2 см распространяется со скоростью v = 15 м/с. Чему равно смещение ξ(x,t) точки, находящейся на расстоянии х = 45 м от источника волн, в тот момент, когда от начала колебаний источника прошло время t = 4 с?

Воспользуемся уравнением плоской волны

. (1)
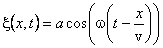
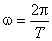
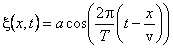
Частота связана с периодом колебаний соотношением . Подставим значение частоты в уравнение (1).

.
Подставляя в последнее выражение численные значения величин, получим

м.

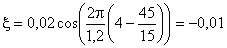
Задача 2. Две точки находятся на расстоянии Δx = 50 см друг от друга на прямой, вдоль которой распространяется плоская волна со скоростью v = 50 м/с. Период колебаний Т равен 0,05 с. Найдите разность фаз Δφ колебаний в этих точках.

Фаза плоской волны равна . Разность фаз в двух точках пространства, охваченного волновым процессом, в момент времени t определяется соотношением

.
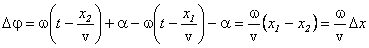
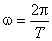
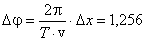
Подставляя численные значения и учитывая, что , получим

рад.

Задача 3. Звуковые колебания, имеющие частоту ν = 0,5 КГц и амплитуду a, равную 0,25 мм, распространяются в упругой среде. Длина волны λ = 70 см. Найдите:

1. скорость распространения волн;

2. максимальную скорость частиц среды.

Скорость распространения волны связана с длиной волны соотношением

λ = v·T, (2)
где Т — период колебаний частиц среды. Период колебаний связан с частотой колебаний ν соотношением

. (3)
Из (2) и (3) получим для скорости распространения волны

v = λ·ν = 350 м/с.
Для ответа на второй вопрос воспользуемся уравнением плоской волны

.
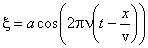
Чтобы найти скорость частиц среды, нужно взять производную от смещения по времени

.
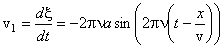
Отсюда видно, что максимальная скорость движения частиц среды будет равна

Задача 4. Две волны ξ₁ = asin(ωt-kx) и ξ₂ = asin(ωt+kx) с одинаковыми частотами ν = 4 Гц распространяются со скоростью v = 960 см/с. Они интерферируют между собой и образуют стоячую волну. Определите амплитуду точек стоячей волны через каждые l = 20 см, начиная отсчет от узла. Определите величину смещения и скорость этих точек в момент времени 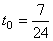с.

Стоячая волна возникает в результате интерференции при сложении ξ₁ и ξ₂.

ξ = ξ₁+ξ₂ = 2acos(kx)sin(2πνt).
Из уравнения стоячей волны видно, что в каждой точке пространства происходят колебания с частотой ω. При этом амплитуда колебаний в точке х равна

A = 2a|coskx|.
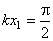
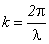
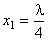
Следовательно, в точках, в которых coskx = 0 , колебания отсутствуют. Эти точки являются узлами стоячей волны. Координата первого узла определяется из соотношения . Учитывая, что , получим . Расстояние между двумя соседними узлами равно см.

Следовательно, между двумя узлами будет находиться n = 5 точек, удовлетворяющих условию задачи. Координаты этих точек будут равны

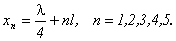
Амплитуда колебаний в этих точках определяется из условия:

.
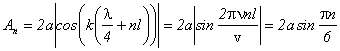
Подставляя значения n, получим A₁ = a , A₂ = 1,73a , A₃ = 2a , A₄ = 1,73a , A₅ = a .

Смещение найденных точек от положения равновесия можно найти из уравнения стоячей волны.

.
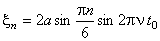
Подставляя численные значения, получим ξ₁ = 0,866a , ξ₂ = 1,5a , ξ₃ = 1,732a , ξ₄ = 1,5a , ξ₅ = 0,866a .
Чтобы найти скорость этих точек, нужно взять производную от смещения ξ по времени

.
Подставляя численные значения, получим: V₁ = 1,566a , V₂ = 2,174a , V₃ = 3,132a , V₄ = 2,174a , V₅ = 1,566a .

Задача 5. В упругой однородной среде распространяются две плоские волны — одна вдоль оси Х, другая вдоль оси Y: ξ₁ = acos(ωt-kx), ξ₂ = acos(ωt-ky). Найдите характер движения частиц среды в плоскости XY, если обе волны поперечные и направление колебаний одинаково.

Воспользуемся принципом суперпозиции волн, тогда результирующий волновой процесс будет описываться уравнением:

.
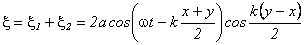
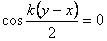
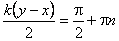
Из полученного уравнения видно, что в точках, для которых выполняется условие , колебания отсутствуют. Координаты этих точек будут удовлетворять условию , где n = 0, 1, 2, …
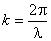
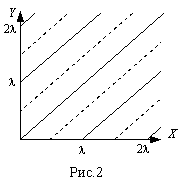
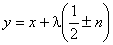
Учитывая, что волновое число , получим, что частицы среды не совершают колебания вдоль прямых, уравнения которых имеет вид

.
На рис. 2 эти прямые проведены пунктиром.

Если , частицы среды колеблются с максимальным отклонением. Этому условию удовлетворяют точки, координаты которых можно получить из условия , где n = 0, 1, 2, … После подстановки значения получим уравнение прямых y = x ± nλ. На рис. 2 эти прямые проведены сплошными линиями.

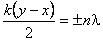
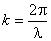
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармоническое колебательное движение и волны

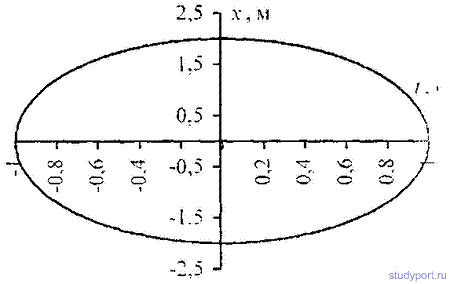
12.41. Точка участвует в двух взаимно перпендикулярных колебаниях x = sinPt и y = 2sin(Pt+P/2). Найти траекторию результирующего движения точки.

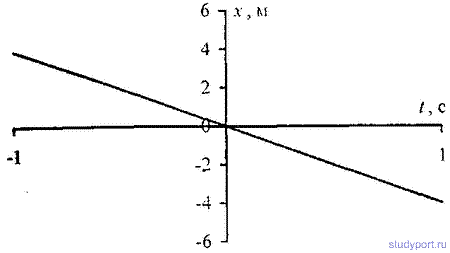
12 42. Точка участвует в двух взаимно перпендикулярных колебаниях х = sinPt a y = 4sin(Pt + P). Найти траекторию результирующего движения точки и начертить ее с нанесением масштаба.

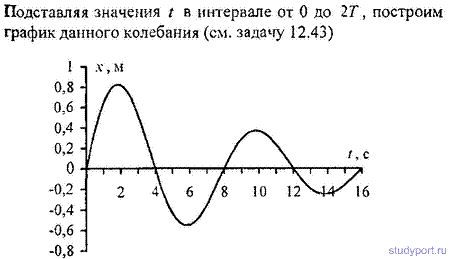
12.43. Период затухающих колебаний T = 4с; логарифмический декремент затухания N = 1.6; начальная фаза φ = 0. При t=T/4 смещение точки x = 4,5 см. Написать уравнение движения

этого колебания. Построить график этого колебания в пределах двух периодов.

12.44. Построить график затухающего колебания, данного

уравнением x=5e -0,1t sinP/4t м.

12.45. Уравнение затухающих колебаний дано в виде x=5e -0,25t sinP/2tм. Найти скорость v колеблющейся точки в моменты времени t, равные: 0, T, 2T, 3Т и 4T,

12.46. Логарифмический декремент затухания математического маятника N = 0.2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?

12.47. Найти логарифмический декремент затухания математического маятника, если за время t = 1мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника l= 1м.

12.48. Математический маятник длиной l = 24,7 см совершает затухающие колебания. Через какое время t энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания: а) N = 0,01; б) N = 1.

12.49. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания N = 0,2 . Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?

12.50. Амплитуда затухающих колебаний математического маятника за время t = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t = 3 мин?

12.51. Математический маятник длиной l = 0,5м, выведенный из положения равновесия, отклонился при первом колебании на х₁ = 5 см, а при втором ( в ту же сторону) — на x₂ = 4см. Найти время релаксации t, т. е. время, в течение которого амплитуда колебаний уменьшится в е раз, где е — основание натуральных логарифмов.

12.52. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на dl = 9,8см. Оттягивая этот груз вниз и отпуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания δ, чтобы: а) колебания прекратились через время t = 10 с (считать условно, что колебания прекратились, если их амплитуда упала до 1% от начальной); б) груз возвращается в положение равновесия апериодически; в) логарифмический декремент затухания колебаний был равным N = 6 ?

12.53. Тело массой m = 10 г совершает затухающие колебания с максимальной амплитудой A_max = 7см, начальной фазой φ = о и коэффициентом затухания δ = 1,6 см -1 . На это тело начала действовать внешняя периодическая сила F, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид х = 5sin(10Pt-3P/4) см. Найти (с числовыми коэффициентами) уравнение собственных колебаний и уравнение внешней периодической силы.

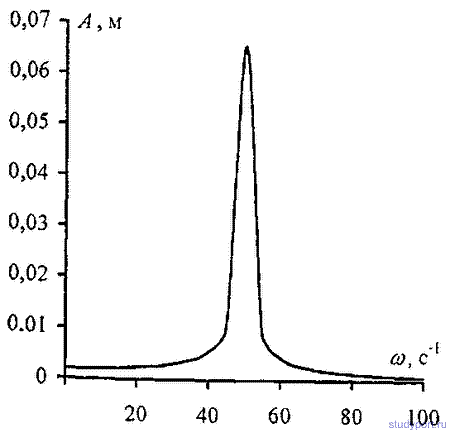
12.54. Гиря массой m = 0,2 кг, висящая на вертикальной пружине, совершает затухающие колебания с коэффициентом затухания δ= 0,75 см -1 . Жесткость пружины k = 0,5кН/м. Начертить зависимость амплитуды А вынужденных колебаний гирьки от частоты внешней периодической силы, если известно, что максимальное значение внешней силы F₀ = 0,98 Н. Для построения .трафика найти значение А для частот: w= 0, w= 0,5, w = 0,75, w = w₀, w = w=1,5w₀ и w = 2w₀, где w₀— частота собственных колебаний подвешенной гири.

12.55. По грунтовой дороге прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии l = 30 см друг от друга. По этой дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на x₀ = 2 см под действием груза массой m₀ = 1 кг. С какой скоростью v катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски M= 10 кг.

12.56. Найти длину волны λ колебания, период которого T = 10 -14 с. Скорость распространения колебаний с = 3 * 10 8 м с.

12.57. Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду A =0.25 мм. распространяются в воздухе. Длина волны λ = 70 см. Найти скорость с распространения колебаний и максимальную скорость V_max частиц воздуха.

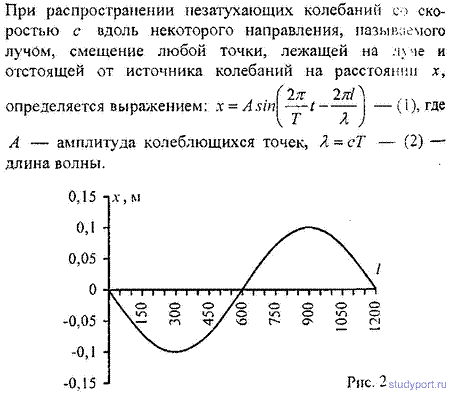
12.58. Уравнение незатухающих колебаний имеет вид

x=10sinP/2*t см. Найти уравнение волны, если скорость распространения колебаний с = 300м*с. Написать и изобразить графически уравнение колебания для точки, отстоящей на расстоянии

l = 600 м от источника колебаний. Написать и изобразить графически уравнение колебания для точек волны в момент времени t= 4 с после начала колебаний.

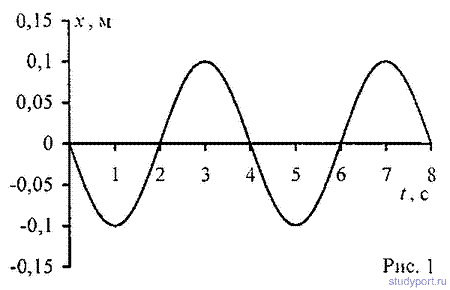
12.59. Уравнение незатухающих колебаний имеет вид x = 4sin600Pt см. Найти смещение x от положения равновесия

точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01 с после начала колебаний. Скорость распространения колебаний с = 300 м/с.

12.60. Уравнение незатухающих колебаний имеет вид x=sin2,5Pt см. Найти смещение х от положения равновесия, скорость v и ускорение a точки, находящейся на расстоянии

l = 20м от источника колебаний, для момента времени t = 1с после начала колебаний. Скорость распространения колебаний с = 100 м*с.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

4. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

Гармонические колебания происходят по закону:

Где X – смещение частицы от положения равновесия, А – амплитуда колебаний, ω – круговая частота, φ0 – начальная фаза, T – время.

Период колебаний T = .

Скорость колеблющейся частицы:

υ = = – A ω sin (ωT + φ0),

Ускорение A = = – Aω2 cos (ωT + φ0).

Кинетическая энергия частицы, совершающей колебательное движение: EK = = sin2(ωT + φ0).

EN = cos2(ωT + φ0).

Периоды колебаний маятников

– пружинного T = ,

Где M – масса груза, K – коэффициент жесткости пружины,

– математического T = ,

Где L – длина подвеса, G – ускорение свободного падения,

– физического T = ,

Где I – момент инерции маятника относительно оси, проходящей через точку подвеса, M – масса маятника, L – расстояние от точки подвеса до центра масс.

Приведенная длина физического маятника находится из условия: LNp = ,

Обозначения те же, что для физического маятника.

При сложении двух гармонических колебаний одной частоты и одного направления получается гармоническое колебание той же частоты с амплитудой:

И начальной фазой: φ = arctg .

Где А1, A2 – амплитуды, φ1, φ2 – начальные фазы складываемых колебаний.

Траектория результирующего движения при сложении взаимноперпендикулярных колебаний одной частоты:

+ – cos (φ2 – φ1) = sin2 (φ2 – φ1).

Затухающие колебания происходят по закону:

Где β – коэффициент затухания, смысл остальных параметров тот же, что для гармонических колебаний, А0 – начальная амплитуда. В момент времени T амплитуда колебаний:

Логарифмическим декрементом затухания называют:

λ = ln = βT,

Где Т – период колебания: T = .

Добротностью колебательной системы называют:

D = .

Уравнение плоской бегущей волны имеет вид:

Y = Y0 cos ω(T ± ),

Где У – смещение колеблющейся величины от положения равновесия, У0 – амплитуда, ω – круговая частота, T – время, Х – координата, вдоль которой распространяется волна, υ – скорость распространения волны.

Знак «+» соответствует волне, распространяющейся против оси X, знак «–» соответствует волне, распространяющейся по оси Х.

Длиной волны называют ее пространственный период:

Где υ–скорость распространения волны, T–период распространяющихся колебаний.

Уравнение волны можно записать:

Y = Y0 cos 2π ( + ).

Стоячая волна описывается уравнением:

Y = (2Y0 cos ) cos ω T.

В скобки заключена амплитуда стоячей волны. Точки с максимальной амплитудой называются пучностями,

XП = N,

Точки с нулевой амплитудой – узлами,

XУ = (N + ) .

Примеры решения задач

Амплитуда гармонических колебаний равна 50 мм, период 4 с и начальная фаза . а) Записать уравнение этого колебания; б) найти смещения колеблющейся точки от положения равновесия при T=0 и при T = 1,5 с; в) начертить график этого движения.

Уравнение колебания записывается в виде X = A cos(wT + j0).

По условию известен период колебаний. Через него можно выразить круговую частоту w = . Остальные параметры известны:

А) X = 0,05 cos(T + ).

Б) Смещение X при T = 0.

X1 = 0,05 cos= 0,05 = 0,0355 м.

X2 = 0,05 cos( 1,5 + )= 0,05 cos p = – 0,05 м.

В) график функции X=0,05cos (T + ) выглядит следующим образом:

Определим положение нескольких точек. Известны Х1(0) и Х2(1,5), а также период колебаний. Значит, через DT = 4 c значение Х повторяется, а через DT = 2 c меняет знак. Между максимумом и минимумом посередине – 0 .

Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно 25 мм.

1 способ. Записываем уравнение колебания точки:

X = 0,05 cos p T, т. к. w = = p.

Находим скорость в момент времени T:

υ = = – 0,05 cos p T.

Находим момент времени, когда смещение равно 0,025 м:

0,025 = 0,05 cos p t1,

Отсюда cos pT1 = , pT1 = . Подставляем это значение в выражение для скорости:

υ = – 0,05 p sin = – 0,05 p = 0,136 м/c.

2 способ. Полная энергия колебательного движения:

E = ,

Где А – амплитуда, w – круговая частота, M – масса частицы.

В каждый момент времени она складывается из потенциальной и кинетической энергии точки

EK = , EП = , но K = MW2, значит, EП = .

Запишем закон сохранения энергии:

= + ,

Отсюда получаем: A2w2 = υ 2 + w2X2,

υ = w = p = 0,136 м/c.

Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия Е = 3∙10-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25∙10-5 Н?

Полная энергия точки, совершающей гармонические колебания, равна: E = . (13)

Модуль упругой силы выражается через смещение точек от положения равновесия X следующим образом:

В формулу (13) входят масса M и круговая частота w, а в (14) – коэффициент жесткости K. Но круговая частота связана с M и K:

Отсюда K = MW2 и F = MW2X. Выразив MW2 из соотношения (13) получим: MW2 = , F = X.

Откуда и получаем выражение для смещения X: X = .

Подстановка числовых значений дает:

X = = 1,5∙10-2 м = 1,5 см.

Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А1 = 3 см и А2 = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания происходят в одном направлении; 2) колебания взаимно перпендикулярны.

1) Если колебания происходят в одном направлении, то амплитуда результирующего колебания определится как:

A = ,

Где А1 и А2 – амплитуды складываемых колебаний, j1 и j2–начальные фазы. По условию начальные фазы одинаковы, значит j2 – j1 = 0, а cos 0 = 1.

A = == А1+А2 = 7 см.

2) Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:

Cos(j 2 – j 1) = sin2(j 2 – j 1).

Так как по условию j2 – j1 = 0, cos 0 = 1, sin 0 = 0, то уравнение запишется в виде: =0,

Или =0,

Или .

Уравнение волны в момент времени t 4 после начала колебаний

Полученное соотношение между X и У Можно изобразить на графике. Из графика видно, что результирующим будет колебание точки на прямой MN. Амплитуда этого колебания определится как: A = = 5 см.

Период затухающих колебаний Т=4 с, логарифмический декремент затухания l = 1,6 , начальная фаза равна нулю. Смещение точки при T = равно 4,5 см. 1) Написать уравнение этого колебания; 2) Построить график этого движения для двух периодов.

1) Уравнение затухающих колебаний с нулевой начальной фазой имеет вид:

X = A0E — bT cos2p.

Для подстановки числовых значений не хватает величин начальной амплитуды А0 и коэффициента затухания b.

Коэффициент затухания можно определить из соотношения для логарифмического декремента затухания:

Таким образом b = = = 0,4 с-1.

Начальную амплитуду можно определить, подставив второе условие:

4,5 см = A0 cos 2p = A0 Cos = A0 .

A0 = 4,5∙ (см) = 7,75 см.

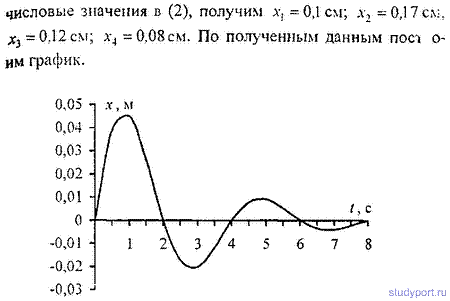
Окончательно уравнение движения:

X = 0,0775 CosT.

2) Для построения графика сначала рисуем огибающую X = 0,0775 , а затем колебательную часть.

Чему равен логарифмический декремент затухания математического маятника, если за T = 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника L = 1 м.

Логарифмический декремент затухания можно найти из соотношения: l= bТ,

Где b – коэффициент затухания, Т – период колебаний. Собственная круговая частота математического маятника:

W0 = = 3,13 с-1.