Одномерные волны: математическое выражение и примеры — Наука
- Содержание:
- Примеры одномерных волн и неодномерных волн
- Одномерные волны
- Неодномерные волны
- Математическое выражение одномерной волны.
- Одномерное волновое уравнение
- Пример работы
- Решение для)
- Решение б)
- Решение c)
- Ссылки
- БИЛЕТ 18.Волновое движение. Плоская гармоническая волна. Длина волны, волновое число. Фазовая скорость. Уравнение волны. Одномерное волновое уравнение.
- Уравнение волны одномерное волновое уравнение
- Волновое уравнение Wave equation
- 📺 Видео
Видео:Уравнения математической физики. Одномерное волновое уравнение. Метод Фурье.Скачать

Содержание:
В одномерные волны Это те, которые распространяются в одном направлении, независимо от того, происходит ли вибрация в том же направлении распространения или нет. Хорошим примером этого является волна, которая проходит через тугую струну, как у гитары.
В плоской волнепересекать, частицы колеблются в вертикальном направлении (они движутся вверх и вниз, см. красную стрелку на рисунке 1), но это одномерно, поскольку возмущение распространяется только в одном направлении, следуя желтой стрелке.
Одномерные волны в повседневной жизни возникают довольно часто. В следующем разделе описаны некоторые их примеры, а также не одномерные волны, чтобы четко установить различия.
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Примеры одномерных волн и неодномерных волн
Видео:Уравнения математической физики. Одномерное волновое уравнениеСкачать

Одномерные волны
Вот несколько примеров одномерных волн, которые можно легко наблюдать:
— Звуковой импульс, который проходит через прямую полосу, поскольку это возмущение, которое распространяется по всей длине полосы.
— Волна, которая проходит через канал с водой, даже если водная поверхность перемещается не параллельно каналу.
— Волны, распространяющиеся по поверхности или в трехмерном пространстве, также могут быть одномерными, если их волновые фронты параллельны друг другу и распространяются только в одном направлении.
Видео:Колебания и волны | волны | волновое уравнение | 1Скачать

Неодномерные волны
Пример неодномерной волны можно найти в волнах, которые образуются на поверхности неподвижной воды, когда падает камень. Это двумерная волна с цилиндрическим волновым фронтом.
Другой пример неодномерной волны — звуковая волна, которую фейерверк генерирует, взрываясь на определенной высоте. Это трехмерная волна со сферическими волновыми фронтами.
Видео:Уравнения математической физики. Решение Даламбера одномерного волнового уравненияСкачать

Математическое выражение одномерной волны.
Самый общий способ выразить одномерную волну, которая распространяется без затухания в положительном направлении оси. Икс и со скоростью v математически:
В этом выражении Y представляет нарушение положения Икс Мгновенно т. Форма волны задается функцией F. Например, волновая функция, показанная на рисунке 1: y (x, t) = cos (x — v t) а волновой образ соответствует моменту t = 0.
Такая волна, описываемая функцией косинуса или синуса, называется гармоническая волна. Хотя это не единственная существующая форма волны, она чрезвычайно важна, потому что любая другая волна может быть представлена как суперпозиция или сумма гармонических волн. Речь идет об известном Теорема Фурье, поэтому используется для описания сигналов всех видов.
Когда волна движется в отрицательном направлении оси x, она просто меняет v от -v в аргументе, оставив:
у (х, t) = g (х + v t)
На рисунке 3 показана анимация волны, бегущей влево: это форма, называемая функцией.Лоренциана и она математическое выражение:
В этом примере скорость распространения равна v = 1, -Единица пространства для каждой единицы времени-.
Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Одномерное волновое уравнение
Волновое уравнение — это уравнение в частных производных, решением которого, конечно же, является волна. Он устанавливает математические отношения между пространственной и временной частью и имеет вид:
Видео:Классические уравнения | волновое уравнение | элементарнейшие случаи двумерных волнСкачать

Пример работы
Ниже приводится общее выражение y (x, t) для гармонической волны:
а) Опишите физический смысл параметров А, к, ω Y θo.
б) Какое значение имеют знаки ± в аргументе косинуса?
c) Убедитесь, что данное выражение действительно является решением волнового уравнения из предыдущего раздела, и найдите скорость v распространения.
Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Решение для)
Характеристики волны находятся в следующих параметрах:
-ТО представляет амплитуда или «высота волны».
-k находится в волновое число и связана с длиной волны λ через к = 2π / λ.
-ω это fугловая частота и связан с периодТ колебание волны
-θo это Начальная стадия, который связан с начальной точкой волны.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Решение б)
Отрицательный знак принимается, если волна распространяется в положительном направлении оси X, и положительный знак в противном случае.
Видео:Получение уравнения плоской бегущей волны.Скачать

Решение c)
Проверить, что данное выражение является решением волнового уравнения, просто: берется частная производная функции у (х, т) дважды по x, дважды повторно получить частично по t, а затем объединить оба результата, чтобы получить равенство:
Эти результаты подставляются в волновое уравнение:
Так много К поскольку косинус упрощен, так как они появляются по обе стороны от равенства, а аргумент косинуса тот же, поэтому выражение сводится к:
-k 2 = (1 / v 2 ) (-ω 2 )
Что позволяет получить уравнение для v с точки зрения ω Y k:
Видео:4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать

Ссылки
- Электронное обучение. Уравнение одномерных гармонических волн. Получено с: e-ducativa.catedu.es
- Уголок физики. Волновые классы. Получено с: fisicaparatontos.blogspot.com.
- Фигероа, Д. 2006. Волны и квантовая физика. Серия: Физика для науки и техники. Отредактировал Дуглас Фигероа. Университет Симона Боливара. Каракас Венесуэла.
- Лаборатория физики Волновое движение. Получено с: fisicalab.com.
- Пирс, А. Лекция 21: Одномерное волновое уравнение: решение Д’Аламбера. Получено с: ubc.ca.
- Волновое уравнение. Получено с: en.wikipedia.com
Патологическое пристрастие к азартным играм: симптомы, причины, последствия и лечение
Эмпирические знания: что это такое, характеристики, виды и примеры
Видео:Вывод волнового уравненияСкачать

БИЛЕТ 18.Волновое движение. Плоская гармоническая волна. Длина волны, волновое число. Фазовая скорость. Уравнение волны. Одномерное волновое уравнение.
Волновое движение – процесс распространения колебаний в сплошной среде. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Если рассмотреть волновой процесс подробнее, то становится ясным, что колеблются не только частицы, расположенные вдоль оси х, но и совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Бегущая волна – волна, которая переносит в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. — уравнение бегущей волны. — если плоская волна распространяется в противоположном направлении. В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид: , где А — const — амплитуда волны; ɷ —циклическая частота; φ0 — начальная фаза волны; определяемая в общем случае выбором начал отсчета х и t; скорость v распространения волны в уравнении есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью. Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением —дифференциальным уравнением в частных производных — или
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой 
Волново́е число́ (также называемое пространственной частотой) — это отношение 2π радиан к длине волны:
Одномерное волновое уравнение – уравнение, описывающее продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня (струны) и другие задачи.
БИЛЕТ 20 Интерференционное поле от двух точечных источников. Опыт Юнга. Интерферометр Майкельсона. Интерференция в тонких пленках. Стоячие волны.
Для получения когерентных источников света французский физик Огюстен Френель (1788—1827) нашел в 1815 г. простой и остроумный способ. Надо свет от одного источника разделить на два пучка и, заставив их пройти различные пути, свести вместе. Тогда цуг волн, испущенных отдельным атомом, разделится на двакогерентных цуга. Так будет для цугов волн, испускаемых каждым атомом источника. Свет, испускаемый одним атомом, дает определенную интерференционную картину. При наложении этих картин друг на друга получается достаточно интенсивное распределение освещенностина экране: интерференционную картину можно наблюдать. Имеется много способов получения когерентных источников света, но суть их одинакова. С помощью разделения пучка на две части получают два мнимых источника света, дающих когерентные волны. Для этого используют два зеркала (бизеркала Френеля), бипризму (две призмы, сложенные основаниями), билинзу (разрезанную пополам линзу с раздвинутыми половинами) и др. Условие максимума: Если в оптической разности хода волн укладывается четное число полуволн или целое число волн, то в данной точке экрана наблюдается усиление интенсивности света (max): 
В этом опыте Юнг поток света направил на непрозрачную пластинку с двумя очень маленькими отверстиями, за которой находился экран. Если придерживаться господствовавшей в то время корпускулярной теории света, то на экране он должен был увидеть две светящиеся точки. Вместо этого на экране он увидел чередующиеся светлые и тёмные полосы. Причём самая яркая из них находилась на экране посередине между отверстиями на перегородке, чего быть вообще-то не должно. Юнг объяснил возникновение полос явлением интерференции света. На экране светлые полосы соответствуют точкам, в которых фазы волн одинаковы, а тёмные — точкам, в которых фазы волн противоположны.
Интерферометр Майкельсона — двухлучевой интерферометр, изобретённый Альбертом Майкельсоном. Данный прибор позволил впервые [1] измеритьдлину волны света. В опыте Майкельсона интерферометр был использован Майкельсоном для проверки гипотезы о светоносном эфире. [1]
Конструктивно состоит из светоделительного зеркала, разделяющего входящий луч на два, которые в свою очередь, отражаются зеркалом обратно. На полупрозрачном зеркале разделённые лучи вновь направляются в одну сторону, чтобы, смешавшись на экране, образовать интерференционную картину. Анализируя её и изменяя длину одного плеча на известную величину, можно по изменению вида интерференционных полос измерить длину волны, либо, наоборот, если длина волны известна, можно определить неизвестное изменение длин плеч. Радиус когерентности изучаемого источника света или другого излучения определяет максимальную разность между плечами интерферометра.
Интерференционные полосы равного наклона. При освещении тонкой пленки происходит наложение волн от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала
Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называетсястоячей волной. Практически стоячие волны возникают при отражении от преград.
Видео:Колебания и волны | волны | волновое уравнение | 3Скачать

Уравнение волны одномерное волновое уравнение
Волновое уравнение
Wave equation
Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением
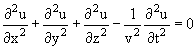 | (1) |
где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид
u(x,t) = Asin(ωt − xv).
Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T
Частота ω и период колебаний T связаны соотношением
Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x
u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).
u(r,t) = (A/r)sin(ωt − kr).
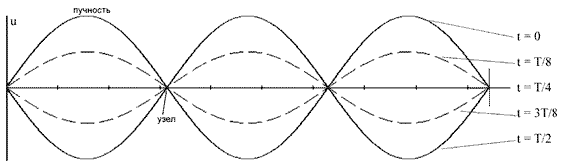
Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.
Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.
| Падающая волна | u1 = Asin(ωt + kx) | |
| Отражённая волна | u2 = Asin(ωt − kx + π) | |
| Стоячая волна | u1 + u2 = A(x)cosωt | (2) |
Соотношение (2) можно получить, используя формулу
sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]
и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.
📺 Видео
4.1 Однородные волновые уравнения ГельмгольцаСкачать

Задача Коши для волнового уравнения (Часть 1)Скачать

Волновое уравнение для волн в упругой среде.Скачать

*** Лекция. Волновое уравнение электромагнитной волны ******Скачать

Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать

Общая физика | Л23: Элементы теории волн. Волновое уравнение. Поперечные и продольные колебанияСкачать