Волновое уравнение
Wave equation
Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением
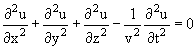 | (1) |
где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид
u(x,t) = Asin(ωt − xv).
Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T
Частота ω и период колебаний T связаны соотношением
Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x
u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).
u(r,t) = (A/r)sin(ωt − kr).
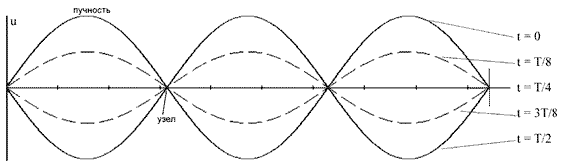
Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.
Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.
| Падающая волна | u1 = Asin(ωt + kx) | |
| Отражённая волна | u2 = Asin(ωt − kx + π) | |
| Стоячая волна | u1 + u2 = A(x)cosωt | (2) |
Соотношение (2) можно получить, используя формулу
sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]
и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Уравнение волны что такое kx
| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать  ВОЛНЫ В УПРУГОЙ СРЕДЕ. АКУСТИКА Основные формулы• Уравнение плоской волны • Длина волны связана с периодом Т колебаний и частотой ν соотношениями •Разность фаз колебаний двух точек среды, расстояние между которыми (разность хода) равно Δx, где λ — длина волны. • Уравнение стоячей волны • Фазовая скорость продольных волн в упругой среде: в твердых телах в газах • Акустический эффект Доплера где ν — частота звука, воспринимаемого движущимся прибором (или ухом); υ — скорость звука в среде; uпр — скорость прибора относительно среды; uист — скорость источника звука относительно среды; ν 0 — частота звука, испускаемого источником. • Амплитуда звукового давления где ν — частота звука; А — амплитуда колебаний частиц среды; υ — скорость звука в среде; ρ — ее плотность. • Средняя объемная плотность энергии звукового поля где ξ0 — амплитуда скорости частиц среды; ω — угловая частота звуковых волн. • Энергия звукового поля, заключенного в некотором объеме V, • Поток звуковой энергии где W — энергия, переносимая через данную поверхность за время t. • Интенсивность звука (плотность потока звуковой энергии) · Интенсивность звука связана со средней объемной плотностью энергии звукового поля соотношением I = J, где J — скорость звука в среде. · Связь мощности N точечного изотропного источника звука с интенсивностью звука где r — расстояние от источника звука до точки звукового поля, в которой определяется интенсивность. · Удельное акустическое сопротивление среды где S — площадь сечения участка акустического поля (например, площадь поперечного сечения трубы при распространении в ней звука). · Уровень интенсивности звука (уровень звуковой мощности) (дБ) где I0 — условная интенсивность, соответствующая нулевому уровню интенсивности (I0=1 пВт/м 2 ). · Уровень громкости звука LN в общем случае является сложной функцией уровня интенсивности и частоты звука и определяется по кривым уровня громкости (рис. 7.1). На графике по горизонтальной оси отложены логарифмы частот звука (сами частоты указаны под соответствующими им логарифмами). На вертикальной оси отложены уровни интенсивности звука в децибелах. Уровни громкости звука отложены по вертикальной оси, соответствующей эталонной частоте v=1000 Гц. Для этой частоты уровень громкости, выраженный в децибелах, равен уровню интенсивности в децибелах. Уровень громкости звуков других частот определяется по кривым громкости, приведенным на графике. Каждая кривая соответствует определенному уровню громкости. Кривые уровней громкости Примеры решения задач Пример 1. Поперечная волна распространяется вдоль упругого шнура со скоростью J=15 м/с. Период Т колебаний точек шнура равен 1,2 с, амплитуда A=2 см. Определить: 1) длину волны l; 2) фазу j колебаний, смещение x, скорость Решение. 1. Длина волны равна расстоянию, которое волна проходит за один период, и может быть найдена из соотношения Подставив значения величин J и T, получим 2. Запишем уравнение волны: где x — смещение колеблющейся точки; х — расстояние точки от источника волн; J — скорость распространения волн. Фаза колебаний точки с координатой х в момент времени tопределяется выражением, стоящим в уравнении волны под знаком косинуса: где учтено, что w=2p/Т. Произведя вычисления по последней формуле, получим j=5,24 рад, или j=300°. Смещение точки определим, подставив в уравнение (1) значения амплитуды А и фазы j: x=1 см. Скорость Ускорение есть первая производная от скорости по времени, поэтому Произведя вычисления по этой формуле, найдем 3. Разность фаз Dj колебаний двух точек волны связана с расстояниемDх между этими точками соотношением Подставив значения величин l, x1 и x2 и вычислив, получим Dj=3,49 рад, или Dj=200°.
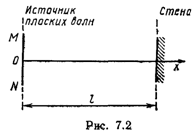
Пример 2. На расстоянии l=4 м от источника плоской волны частотой v=440 Гц перпендикулярно ее лучу расположена стена. Определить расстояния от источника волн до точек, в которых будут первые три узла и три пучности стоячей волны, возникшей в результате сложения бегущей и отраженной от стены волн. Скорость J волны считать равной 440 м/с. Решение. Выберем систему координат так, чтобы ось х была направлена вдоль луча бегущей волны и начало О координат совпадало с точкой, находящейся на источнике MN плоской волны (рис. 7.2). С учетом этого, уравнение бегущей волны запишется в виде Поскольку в точку с координатой х волна возвратится, прейдя дважды расстояние l—х, и при отражении от стены, как среды более плотной, изменит фазу на p, то уравнение отраженной волны может быть записано в виде После очевидных упрощений получим x2=Acоs[wt—k (2l—х)]. 2) Сложив уравнения (1) и (2), найдем уравнение стоячей волны: Воспользовавшись формулой разности косинусов, найдем Так как выражение Asink(l—х) не зависит от времени, то, взятое по модулю, оно может рассматриваться как амплитуда стоячей волны: Зная выражение амплитуды, можем найти координаты узлов и пучностей. Узлы возникнут в тех точках, где амплитуда стоячей волны равна нулю:|2Asink(l—x)|=0. Это равенство выполняется для точек, координаты xn которых удовлетворяют условию Но k=2p/l, или, так как l=J/v, k=2pv/J. (4) Подставив это выражение k в (3), получим откуда координаты узлов Подставив сюда значения l,J, v и n=0, 1, 2, найдем координаты первых трех узлов: Пучности возникнут в тех точках, где амплитуда стоячей волны максимальна: 2Asink(l—х‘)=2А. Это равенство выполняется для точек, координаты х‘n которых удовлетворяют условию k(l— х‘n)=(2n+1)(p/2) (п=0, 1, 2, 3, . ). Выразив здесь k по (4), получим откуда координаты пучностей Подставив сюда значения l, J, v и n=0, 1, 2, найдем координаты первых трех пучностей:
Границы максимальных смещений точек среды в зависимости от их координат изображены на рис. 7.3. Здесь же отмечены координаты х0,, х1, х2 , . узлов и координаты х‘0, х‘1, х‘2 . пучностей стоячей волны.
Пример 3. Источник звука частотой v=18 кГц приближается к неподвижно установленному резонатору, настроенному на акустическую волну длиной l= 1,7 см. С какой скоростью должен двигаться источник звука, чтобы возбуждаемые им звуковые волны вызвали колебания резонатора? Температура T воздуха равна 290 К. Решение. Согласно принципу Доплера, частота v звука, воспринимаемая прибором (резонатором), зависит от скорости иистисточника звука и скорости ипр прибора. Эта зависимость выражается формулой где J — скорость звука в данной среде; v0 — частота звуковых волн, излучаемых источником. Учитывая, что резонатор остается неподвижным (uпр=0), из формулы (1) получим В этом выражении неизвестны значения скорости J звука и частоты v. Скорость звука в газах зависит от природы газа и температуры и определяется по формуле Чтобы волны, приходящие к резонатору, вызвали его колебания, частота v воспринимаемых резонатором волн должна совпадать с собственной частотой vрезрезонатора, т. е. где vрез —длина волны собственных колебаний резонатора. Подставив выражения J и v из равенства (3) и (4) в формулу (2), получим Взяв значения g=1,4, М ==0,029 кг/моль, а также значения R, Т, vo, lрез и подставив их в последнюю формулу, после вычислений получим Пример 4. Уровень громкости ln звука двух тонов с частотами v1=50 Гц и v2=400 Гц одинаков и равен 10 дБ. Определить уровень интенсивности Lр и интенсивность I звука этих тонов. Решение. Искомые в задаче уровни интенсивности, соответствующие частотам v1=50 Гц и v2=400 Гц, определим, пользуясь графиком на рис. 7.1. Вторая кривая снизу является кривой уровня громкости, равного 10 дБ. Из точек на горизонтальной оси, соответствующих частотам v1 и v2, восстанавливаем ординаты до кривой уровня громкости в 10 дБ. Значения этих ординат укажут искомые уровни интенсивности: Lр1=60 дБ для частоты v1=50 Гц и Lр2=20 дБ для частоты v2=400 Гц. Зная уровни интенсивностей Lр1 и Lр2, определим соответствующие им интенсивности I1 и I2 по формуле где I — интенсивность данного звука; I0 — интенсивность, соответствующая нулевому уровню интенсивности (I0=1 пВт/м 2 ). Из приведенной формулы получим Подставив сюда значения Lр и I0 и учтя, что 1 пВт/м 2 =lO -12 Bт/м 2 , найдем для v1=50 Гц и v2=400 Гц соответственно lgI1=0,l×60+lg10 -12 =6-12= -6; I1=10 -6 Вт/м 2 и lg I2=0.1×20+lgl0 -12 =2-12= -10; I2=10 -10 Вт/м 2 . Эти значения I1 и I2 можно получить и по графику, пользуясь шкалой интенсивности звука (на рис. 7.1 правая шкала). Сопоставим полученные результаты: интенсивность первого тона в 10 4 раз больше интенсивности второго тона; уровень интенсивности первого тона на 40 дБ больше уровня интенсивности второго тона; уровень громкости обоих тонов одинаков и равен 10 дБ. Задачи Уравнение плоской волны 7.1. Задано уравнение плоской волны x(х,t)=Acos(wt—kx), где A=0,5 см, (w=628c -1 ,k=2 м -1 . Определить: 1) частоту колебаний v и длину волны l 2) фазовую скорость J; 3) максимальные значения скорости 7.2. Показать, что выражение x(х,t)=Acos(wt—kx) удовлетворяет волновому уравнению 7.3. Плоская звуковая волна возбуждается источником колебаний частоты v=200 Гц. Амплитуда А колебаний источника равна 4 мм. Написать уравнение колебаний источника x(0,t), если в начальный момент смещение точек источника максимально. Найти смещение x(х,t) точек среды, находящихся на расстоянии x=100 см от источника, в момент t=0,1 с. Скорость J звуковой волны принять равной 300 м/с. Затуханием пренебречь. 7.4. Звуковые колебания, имеющие частоту v=0,5 кГц и амплитуду A=0,25 мм, распространяются в упругой среде. Длина волны l=70 см. Найти: 1) скорость J распространения волн; 2) максимальную скорость 7.5. Плоская звуковая волна имеет период Т=3 мс, амплитуду A=0,2 мм и длину волны l=1,2 м. Для точек среды, удаленных от источника колебаний на расстояние х=2 м, найти: 1) смещение x(х,t) в момент t=7 мс; 2) скорость 7.6. От источника колебаний распространяется волна вдоль прямой линии. Амплитуда A колебаний равна 10 см. Как велико смещение точки, удаленной от источника на х=¾l, в момент, когда от начала колебаний прошло время t=0,9 Т? 7.7. Волна с периодом Т=1,2с и амплитудой колебаний A=2 см распространяется со скоростью J=15 м/с. Чему равно смещение x(х,t) точки, находящейся на расстоянии x=45 м от источника волн, в тот момент, когда от начала колебаний источника прошло время t=4 с? 7.8. Две точки находятся на расстоянии Dх=50 см друг от друга на прямой, вдоль которой распространяется волна со скоростью J=50 м/с. Период Т колебаний равен 0,05 с. Найти разность фаз Dj колебаний в этих точках. 7.9. Определить разность фаз Dj колебаний источника волн, находящегося в упругой среде, и точки этой среды, отстоящей на х=2 м от источника. Частота v колебаний равна 5 Гц; волны распространяются со скоростью J=40 м/с. 7.10. Волна распространяется в упругой среде со скоростью J=100 м/с Наименьшее расстояние Dх между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту v колебаний. 7.11. Определить скорость J распространения волны в упругой среде, если разность фаз Dj колебаний двух точек среды, отстоящих друг от друга на Dх=10 см, равна p/3. Частота v колебаний равна 25 Гц. 7.12. Найти скорость J распространения продольных упругих колебаний в следующих металлах: 1) алюминии; 2) меди; 3) вольфраме. 7.13. Определить максимальное и минимальное значения длины l звуковых волн, воспринимаемых человеческим ухом, соответствующие граничным частотам v1=16 Гц и v2=20 кГц. Скорость звука принять равной 340 м/с. 7.14. Определить скорость J звука в азоте при температуре Т=300 К. 7.15. Найти скорость J звука в воздухе при температурах T1=290 К и Т2=350 К. 7.16. Наблюдатель, находящийся на расстоянии l=800 м от источника звука, слышит звук, пришедший по воздуху, на Dt=1,78 с позднее, чем звук, пришедший по воде. Найти скорость J звука в воде, если температура Т воздуха равна 350 К. 7.17. Скорость J звука в некотором газе при нормальных условиях равна 308 м/с. Плотность r газа равна 1,78 кг/м 3 . Определить отношение Сp/Сv для данного газа. 7.18. Найти отношение скоростей J1/J2 звука в водороде и углекислом газе при одинаковой температуре газов. 7.19. Температура Т воздуха у поверхности Земли равна 300 К; при увеличении высоты она понижается на DT=7 мК на каждый метр высоты. За какое время звук, распространяясь, достигнет высоты h=8 км? Суперпозиция волн 7.20. Имеются два источника, совершающие колебания в одинаковой фазе и возбуждающие в окружающей среде плоские волны одинаковой частоты и амплитуды (A1=A2=1 мм). Найти амплитуду А колебаний точки среды, отстоящей от одного источника колебаний на расстоянии x1=3,5 м и от другого — на x2=5,4 м. Направления колебаний в рассматриваемой точке совпадают. Длина волны l=0,6 м. * В задачах, где в условии не указана скорость звука и не заданы величины, по которым ее можно вычислить, значение скорости следует брать из табл. 16. 7.21. Стоячая волна образуется при наложении бегущей волны и волны, отраженной от границы раздела сред, перпендикулярной направлению распространения волны. Найти положения (расстояния от границы раздела сред) узлов и пучностей стоячей волны, если отражение происходит: 1) от среды менее плотной; 2) от среды более плотной. Скорость J распространения звуковых колебаний равна 340 м/с и частота v=3,4 кГц. 7.22. Определить длину l бегущей волны, если в стоячей волне расстояние l между: 1) первой и седьмой пучностями равно 15 см; 2) первым и четвертым узлом равно 15 cм 7.23. В трубе длиной l=1,2 м находится воздух при температуре T=300 К. Определить минимальную частоту vmin возможных колебаний воздушного столба в двух случаях: 1) труба открыта; 2) труба закрыта. 7.24. Широкая трубка, закрытая снизу и расположенная вертикально, наполнена до краев водой. Над верхним отверстием трубки помещен звучащий камертон, частота v колебаний которого равна 440 Гц. Через кран, находящийся внизу, воду медленно выпускают. Когда уровень воды в трубке понижается на DH=19,5 см, звук камертона усиливается. Определить скорость J звука в условиях опыта. 7.25. Один из способов измерения скорости звука состоит в следующем. В широкой трубке A может перемещаться поршень В.Перед открытым концом трубки A, соединенным с помощью резиновой трубки с ухом наблюдателя, расположен звучащий камертон К. (рис. 7.4.). Отодвигая поршень В от конца трубки A, наблюдатель отмечает ряд следующих друг за другом увеличении и уменьшении громкости звука. Найти скорость J звука в воздухе, если при частоте колебаний v=440 Гц двум последовательным усилениям интенсивности звука соответствует расстояние Dl между положениями поршня, равное 0,375 м.
7.26. На рис. 7.5 изображен прибор, служащий для определения скорости звука в твердых телах и газах. В латунном стержне А, зажатом посередине, возбуждаются колебания. При определенном положении легкого кружочка В, закрепленного на конце стержня, пробковый порошок, находящийся в трубке С, расположится в виде небольших кучек на равных расстояниях. Найти скорость J звука в латуни, если расстояние и между кучками оказалось равным 8,5 см. Длина стержня l=0,8 м. 7.27. Стальной стержень длиной l=1 м, закрепленный посередине, натирают суконкой, посыпанной канифолью. Определить частоту v возникающих при этом собственных продольных колебаний стержня. Скорость J продольных волн в стали вычислить. 7.28. Поезд проходит мимо станции со скоростью u=40 м/с. Частота v0 тона гудка электровоза равна 300 Гц. Определить кажущуюся частоту v тона для человека, стоящего на платформе, в двух случаях: 1) поезд приближается; 2) поезд удаляется. 7.29. Мимо неподвижного электровоза, гудок которого дает сигнал частотой v0=300 Гц, проезжает поезд со скоростью и=40 м/с. Какова кажущаяся частота v тона для пассажира, когда поезд приближается к электровозу? когда удаляется от него? 7.30. Мимо железнодорожной платформы проходит электропоезд. Наблюдатель, стоящий на платформе, слышит звук сирены поезда. Когда поезд приближается, кажущаяся частота звука v1=1100 Гц; когда удаляется, кажущаяся частота v2=900 Гц. Найти скорость и электровоза и частоту v0 звука, издаваемого сиреной. 7.31. Когда поезд проходит мимо неподвижного наблюдателя, высота тона звукового сигнала меняется скачком. Определить относительное изменение частоты Dv/v, если скорость и поезда равна 54 км/ч. 7.32. Резонатор и источник звука частотой v0=8 кГц расположены на одной прямой. Резонатор настроен на длину волны l=4,2 см и установлен неподвижно. Источник звука может перемещаться по направляющим вдоль прямой. С какой скоростью u и в каком направлении должен двигаться источник звука, чтобы возбуждаемые им звуковые волны вызвали колебания резонатора? 7.33. Поезд движется со скоростью u=120 км/ч. Он дает свисток длительностью t0=5 с. Какова будет кажущаяся продолжительность t свистка для неподвижного наблюдателя, если: 1) поезд приближается к нему; 2) удаляется? Принять скорость звука равной 348 м/с. * См. сноску на с. 108 7.34. Скорый поезд приближается к стоящему на путях электропоезду со скоростью и=72 км/ч. Электропоезд подает звуковой сигнал частотой v0=0,6 кГц. Определить кажущуюся частоту v звукового сигнала, воспринимаемого машинистом скорого поезда. 7.35. На шоссе сближаются две автомашины со скоростями u1=30 м/с и u2=20 м/с. Первая из них подает звуковой сигнал частотой v1=600 Гц. Найти кажущуюся частоту v2 звука, воспринимаемого водителем второй автомашины, в двух случаях: 1) до встречи; 2) после встречи. Изменится ли ответ (если изменится, то как) в случае подачи сигнала второй машиной? 7.36, Узкий пучок ультразвуковых волн частотой v0=50 кГц направлен от неподвижноголокатора к приближающейся подводной лодке. Определить скорость и подводной лодки, если частота v1 биений (разность частот колебаний источника и сигнала, отраженного от лодки) равна 250 Гц. Скорость J ультразвука в морской воде принять равной 1,5 км/с. Энергия звуковых волн * 7.37. По цилиндрической трубе диаметром d=20 см и длиной l=5 м, заполненной сухим воздухом, распространяется звуковая волна средней за период интенсивностью I=50 мВт/м 2 . Найти энергию W звукового поля, заключенного в трубе. 7.38. Интенсивность звука 1=1 Вт/м 2 . Определить среднюю объемную плотность энергии звуковой волны, если звук распространяется в сухом воздухе при нормальных условиях. 7.39. Мощность N изотропного точечного источника звуковых волн равна 10 Вт. Какова средняя объемная плотность энергии на расстоянии г=10 м от источника волн? Температуру Т воздуха принять равной 250 К. 7.40. Найти мощность N точечного изотропного источника звука, если на расстоянии r=25 м от него интенсивность I звука равна 20 мВт/м 2 . Какова средняя объемная плотность энергии на этом расстоянии? Звуковое давление. Акустическое сопротивление * 7.41. Определить удельное акустическое сопротивление Zs воздуха при нормальных условиях. 7.42. Определить удельное акустическое сопротивление Zsводы при температуре t=15°C. *См. сноску на с. 108 7.43. Какова максимальная скорость 7.44. Определить акустическое сопротивление Za воздуха в трубе диаметром d=20см при температуре T=300 К и давлении p=200 кПа. 7.45. Звук частотой v=400 Гц распространяется в азоте при температуре T=290 К и давлении p=104 кПа. Амплитуда звукового давления p0=0,5 Па. Определить амплитуду А колебаний частиц азота. 7.46. Определить амплитуду p0 звукового давления, если амплитуда А колебаний частиц воздуха равна 1 мкм. Частота звука v =600 Гц. 7.47. На расстоянии r=100 м от точечного изотропного источника звука амплитуда звукового давления r0=0,2 Па. Определить мощность P источника, если удельное акустическое сопротивление Zs воздуха равно 420 Па×с/м. Поглощение звука в воздухе не учитывать . 7.48. Источник звука небольших линейных размеров имеет мощность Р=1 Вт. Найти амплитуду звукового давления p0 на расстоянии r =100 м от источника звука, считая его изотропным. Затуханием звука пренебречь. 7.49.В сухом воздухе при нормальных условиях интенсивность I звука равна 10пВт/м 2 . Определить удельное акустическое сопротивлениеZs воздуха при данных условиях и амплитуду p0 звукового давления. 7.50. Найти интенсивности I1 и I2 звука, соответствующие амплитудам звукового давления p01=700 мкПа и p02=40 мкПа. Уровень интенсивности, и уровень громкости звука 7.51. Определить уровень интенсивности Lр звука, если его интенсивность равна: 1) 100 пВт/м 2 ; 2) 10 мВт/м 2 . 7.52. На расстоянии r1=24 м от точечного изотропного источника звука уровень его интенсивности Lр=32 дБ. Найти уровень интенсивности Lр звука этого источника на расстоянии r2=16 м. 7.53. Звуковая волна прошла через перегородку, вследствие чего уровень интенсивности Lр звука уменьшился на 30 дБ. Во сколько раз уменьшилась интенсивность I звука? 7.54. Уровень интенсивности Lр шума мотора равен 60 дБ. Каков будет уровень интенсивности, если одновременно будут работать: 1) два таких мотора; 2) десять таких моторов? 7.55. Три тона, частоты которых равны соответственно v1=50 Гц, v2=200 Гц и v3=1кГц, имеют одинаковый уровень интенсивности Lр=40 дБ. Определить уровни громкости LN этих тонов. 7.56. Звук частотой v=1 кГц имеет уровень интенсивности Lр=50 дБ. Пользуясь графиком на рис. 7.1, найти уровни интенсивности равно громких с ним звуков с частотами: v1=l кГц, v2=5 кГц, v3=2 кГц, v4,=300 Гц, v5 =50 Гц. 7.57. Уровень громкости тона частотой v=30 Гц сначала был LN1 =10 фон, а затем повысился до LN2=80 фон. Во сколько раз увеличилась интенсивность тона? 7.58. Пользуясь графиком уровней на рис. 7.1, найти уровень громкости LN звука, если частота v звука равна 2 кГц и амплитуда звукового давления r0=0,1 Па. Условия, при которых находится воздух, нормальные. 7.59. Для звука частотой v=2 кГц найти интенсивность I, уровень интенсивности Lр и уровень громкости LN, соответствующие: а) порогу слышимости; б) порогу болевого ощущения. При решении задачи пользоваться графиком на рис. 7.1. 7.60. Мощность Р точечного изотропного источника звука равна 100 мкВт. Найти уровень громкости LN при частоте v=500 Гц на расстоянии r =10 м от источника звука. 7.61. На расстоянии r =100 м от точечного изотропного источника звука уровень громкости Lр, при частоте v=500 Гц равен 20 дБ. Определить мощность Р источника звука. 🔥 ВидеоКонсультация к устному экзамену. Механика. Часть 9: "Волны"Скачать  Функция y=k/x и ее график. 7 класс.Скачать  *** Лекция. Волновое уравнение электромагнитной волны ******Скачать  Преобразование графиков функций. Сжатие и растяжение. 10 класс.Скачать  Уравнения и графики механических гармонических колебаний. 11 класс.Скачать  Получение уравнения плоской бегущей волны.Скачать  Раскрытие тайн электромагнитной волныСкачать  Билет №34 "Электромагнитные волны"Скачать  Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать  Лекция 2 ВолныСкачать  10й класс; Физика; "Уравнение плоской волны"Скачать  Урок 454. Понятие о волновой функцииСкачать  4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать  Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать  Разбор Механика часть С, способ 2 (уравнение волны)Скачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать  Вывод уравнения электромагнитной волныСкачать  Урок 375. Стоячие волныСкачать  |


 .
. . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)

 .
. ,
, . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или  .
. .
. , или в векторной форме:
, или в векторной форме: ,
, – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности. , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: .
. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: , или
, или  ,
, , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной. , или
, или  ,
,  — смещение точек среды с координатой х в момент времени t; ω — угловая частота; υ — скорость распространения колебаний в среде (фазовая скорость); k — волновое число;
— смещение точек среды с координатой х в момент времени t; ω — угловая частота; υ — скорость распространения колебаний в среде (фазовая скорость); k — волновое число;  ;
;  и
и 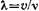

 , или
, или 
 ,
,  ,или
,или  ,
, 

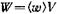
 ,
,

 , и ускорение
, и ускорение  , точки, отстоящей на расстоянии х=45 м от источника волн в момент t=4 с; 3) разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях x1=20 м и x2=30 м.
, точки, отстоящей на расстоянии х=45 м от источника волн в момент t=4 с; 3) разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях x1=20 м и x2=30 м.
 Подставив значения величин p, А, Т и j и произведя вычисления, получим
Подставив значения величин p, А, Т и j и произведя вычисления, получим 


 , откуда
, откуда . (3)
. (3)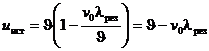 , или
, или  .
. при условии, что w=kJ.
при условии, что w=kJ. Рис. 7.4
Рис. 7.4