Уравнение волнового числа линии в спектрах поглощения следствие закона сохранения энергии (3 видео)

Закон сохранения энергии для волны. Уравнение цилиндрической и сферической волны.

Как видно из раздела 6.3.7, для однозначного задания уравнения гармонической волны необходимо определить ее амплитуду как функцию координат и времени. Даже для стационарного источника амплитуда колебаний частиц в волне, вообще говоря, зависит от расстояния до источника. Во-первых, из-за сил внутреннего трения в среде энергия колебаний переходит в тепло (обычное затухание), а во-вторых, энергия источника ‘‘растекается” по все большей площади. Пусть вначале затухание в среде отсутствует. Тогда поток энергии через замкнутую волновую поверхность площадью 5, окружающую источник, определяется поверхностным интегралом

Понятие потока векторного поля введено в разделе 4.1.4. Поскольку энергия генерируется только источником, закон сохранения энергии требует, чтобы этот поток сохранялся для любой поверхности.

Рассмотрим приведенную на рисунке плоскую волну, порождаемую плоским же источником.

Ввиду параллельности лучей в плоской волне растекания энергии нет. так что

Таким обратом, уравнение плоской волны задается выражением раздела 6.3.7 с постоянной амплитудой.

Рассмотрим теперь сферическую волну, порождаемую сферическим источником (см. рисунок). Как видно из рисунка, теперь энергия растекается по поверхности сферы площадью S = 4кг 2 , поэтому

где Ло — амплитуда на единичном расстоянии от источника. В результате уравнение сферической волны

причем г — радиальная координата.

Аналогично уравнение цилиндрической волны имеет вид

где г — цилиндрическая координата, т.к. в данном случае энергия растекается по поверхности цилиндра, площадь которой S = 2nrh (см. рис.).

При наличии затухания необходимо в формулу для ? ввести сомножитель ехр(—6г), учитывающий потери энергии (б — затухание на единицу длины).

Содержание

Эффект Доплера.
Лабораторная работа: ИССЛЕДОВАНИЕ СОБСТВЕННОГО ОПТИЧЕСКОГО ПОГЛОЩЕНИЯ В ПОЛУПРОВОДНИКАХ
ЛИТЕРАТУРА
Закон сохранения механической энергии
Энергия: что это такое
Механическая энергия
Кинетическая энергия
Потенциальная энергия
Закон сохранения энергии
Переход механической энергии во внутреннюю
Закон сохранения энергии в тепловых процессах
🎬 Видео

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Эффект Доплера.

Указанный эффект состоит в изменении принимаемой частоты волны, связанной с движением источника. Разумеется, ввиду относительного характера движения тот же эффект наблюдается при неподвижном источнике и подвижном приемнике. Если скорость звука в среде у, а скорость движения источника м, то принимаемая частота звука

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Лабораторная работа: ИССЛЕДОВАНИЕ СОБСТВЕННОГО ОПТИЧЕСКОГО ПОГЛОЩЕНИЯ В ПОЛУПРОВОДНИКАХ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Лабораторная работа 3

ИССЛЕДОВАНИЕ СОБСТВЕННОГО ОПТИЧЕСКОГО

ПОГЛОЩЕНИЯ В ПОЛУПРОВОДНИКАХ

Целью работы является освоение методики измерения коэффициента поглощения, определение типа оптических переходов и ширины запрещенной зоны некоторых полупроводников.

При прохождении излучения через вещество интенсивность пучка света уменьшается вследствие отражения и поглощения. Пусть интенсивность падающего света I ₀, отраженного – I _R. Тогда величину

называют коэффициентом отражения. Зависимость коэффициента отражения от длины волны R (λ) или частоты излучения R (ω) называется спектром отражения.

Обозначим интенсивность света, падающего на слой dx , через I . Тогда вследствие поглощения света в этом слое интенсивность излучения уменьшится на величину dI пропорционально количеству падающей на слой энергии и толщине поглощающего слоя:

Коэффициент α называется дифференциальным коэффициентом поглощения. Он имеет размерность обратной длины, и его можно интерпретировать как вероятность поглощения фотона на единичной длине. Обратная величина (α -1 ) имеет смысл длины свободного пробега фотона в поглощающей среде.

Проинтегрировав уравнение (2)

известное под названием закона Бугера-Ламберта. Зависимость коэффициента поглощения от частоты α(ω) или длины волны α(λ) называется спектром поглощения вещества.

Поглощение излучения в полупроводниках может быть связано с изменением энергетического состояния свободных или связанных с атомами электронов, а также с изменением колебательной энергии атомов решетки. В связи с этим в полупроводниках различают пять основных типов оптического поглощения:

1) собственное, связанное с возбуждением электронов из валентной зоны в зону проводимости;

2) экситонное, связанное с образованием экситонов;

3) примесное, обусловленное переходами электронов между примесным уровнем и какой-либо зоной;

4) поглощение свободными носителями заряда, связанное с возбуждением свободных электронов и дырок в пределах одной и той же разрешенной зоны;

5) решеточное, связанное с возбуждением колебаний кристаллической решетки.

Наибольший интерес для диагностики полупроводниковых материалов представляет собственное поглощение. Рассмотрим подробно этот тип поглощения.

Если энергия фотонов где ширина запрещенной зоны, то возможны переходы электронов из валентной зоны (V-зоны) в зону проводимости (С-зону). При этом наблюдается сильное поглощение света полупроводником. Его принято называть собственным или фундаментальным.

1. Прямозонные и непрямозонные полупроводники

В отличие от отдельных атомов и молекул энергетические состояния в твердых телах определяются по всему кристаллу и описываются волновыми функциями типа блоховских функций. Это накладывает особенности на процессы взаимодействия таких систем с электромагнитным излучением. Под оптическими переходами понимают квантовые переходы, совершаемые под действием электромагнитного излучения оптического диапазона.

Рассмотрим квантовый переход из состояния j в состояние f при поглощении фотона ћω и определим, при каких условиях он возможен. Под квантовым переходом понимается скачкообразный переход квантовой системы (атома, молекулы, твердого тела) из одного состояния в другое. При переходе с более высокого уровня энергии E _j на более низкий E _f система отдаёт энергию E _j — E _f , при обратном переходе — получает её. Квантовые переходы могут быть излучательными и безызлучательными. При излучательных квантовых переходах система испускает (переход E _j → E _f ) или поглощает (переход E _f → E _j ) квант электромагнитного излучения.

Возможность квантового перехода между уровнями Е _j и Е _f с заданными характеристиками определяется правилами отбора . Правила отбора устанавливают, какие квантовые переходы разрешены (вероятность перехода велика) и какие запрещены — строго (вероятность перехода равна нулю) или приближённо (вероятность перехода мала).

В результате взаимодействия с фотоном ћω электрон переходит непосредственно из состояния с энергией Е _j в состояние с энергией Е _f. В соответствии с правилом отбора по волновому вектору при непосредственных оптических переходах j → f должно выполняться условие:

где , (- единичный вектор в направлении ). Это соотношение представляет собой закон сохранения волнового вектора или

квазиимпульса (т. к. ).

Для осуществления реального перехода необходимо еще и выполнение закона сохранения энергии. В рассматриваемом случае это приводит к условию:

В общем случае, для непосредственного оптического перехода как с поглощением, так и с испусканием фотона в твердых телах необходимо выполнение двух законов сохранения – энергии и волнового вектора:

Знак плюс соответствует поглощению, а знак минус – испусканию фотона.

Волновой вектор электрона имеет величину π/а 10 8 см -1 . Волновой вектор фотона () в видимой и инфракрасной областях спектра имеет значение 10 5 см -1 (при λ

1мкм). Поэтому >> и, следовательно, выражение (5) приобретает вид

Таким образом, при взаимодействии электрона с фотоном могут осуществляться только переходы без изменения волнового вектора, т. е. между состояниями, расположенными в одной и той же точке –пространства (зоны Бриллюэна). На диаграмме E () такой переход изображается вертикальной линией и называется прямым или вертикальным переходом (рис. 1). В рассматриваемом случае в результате поглощения фотона в зоне проводимости появляется свободный электрон, а в валентной зоне – дырка.

Рис. 1. Прямой оптический переход из j — состояния валентной зоны в f -состояние зоны проводимости с поглощением фотона ћω.

Если f и j состояния принадлежат, например, одной долине (подзоне) с-зоны или v -зоны или различным зонам, экстремумы которых расположены в разных точках зоны Бриллюэна, то непосредственный переход j → f между этими состояниями невозможен. Однако переход f → j состояния допускается в случае, когда переход осуществляется через промежуточное виртуальное состояние. Так как взаимодействие только с фотоном практически не изменяет волнового вектора электрона, то для осуществления перехода f ↔ j при требуется дополнительный процесс, приводящий к рассеянию волнового вектора.

Таким образом, для реализации оптического перехода из j — в f -состояние с существенно различными значениями волновых векторов и необходим дополнительный процесс рассеяния с участием какого-либо рассеивающего центра или квазичастицы, взаимодействие с которой способно изменить волновой вектор электрона (или дырки). Такими квазичастицами и рассеивающими центрами могут быть кванты колебаний кристаллической решетки (фононы), свободные носители заряда (электроны и дырки), примесные атомы, границы раздела и т. д.

Оптические переходы между состояниями с различными называются непрямыми. Так как в непрямых переходах должно участвовать большее число частиц (электрон, фотон и фонон), чем при прямых переходах (электрон и фотон), то вероятность непрямых переходов, а значит, и коэффициент поглощения должны быть меньше, чем для прямых переходов.

На рис. 2 изображен оптический переход j →f , определяющий процесс поглощения фотона ћω с рассеянием за счет взаимодействия с фононом ћω _q . Под воздействием электромагнитного возмущения электрон переходит из валентной зоны, поглощая фотон путем прямого перехода в виртуальное состояние в зоне проводимости. Таким состоянием должно быть реально существующее, например, более высоко лежащее состояние с-зоны. Время пребывания электрона в этом промежуточном состоянии чрезвычайно мало. При переходе в виртуальное состояние закон сохранения энергии не соблюдается.

Рис.2. Процесс поглощения фотона непрямым переходом через промежуточное виртуальное состояние. Пунктиром показан переход с поглощением фонона, а сплошными стрелками — переход с испусканием фонона.

На второй стадии электрон переходит из виртуального состояния зоны проводимости в конечное состояние в экстремум Е _с , испуская или поглощая фонон.

Полный переход j →f возможен, если соблюдаются законы сохранения энергии и волнового вектора, которые для непрямых переходов принимают вид:

где знаки ± соответствуют поглощению и испусканию фонона.

Теперь мы получим два различных значения энергии для особой точки Е ₀ = ћω ₀ в зависимости от того, идет процесс с поглощением или с испусканием фонона. Из рис. 1.6 следует, что при поглощении фотона , (9)

где минус соответствует поглощению фонона, а плюс — испусканию фонона.

На рис. 3 справа представлен оптический переход с испусканием фотона ћω за счет взаимодействия с фононом ħ Ω . Такой переход обладает значительно меньшей вероятностью, чем прямой переход.

Рис. 3. Прямые (слева) и непрямые (справа) межзонные

Для оптоэлектронных устройств предпочтительнее использовать полупроводниковые соединения с прямозонной энергетической структурой, спектральный диапазон которых лежит в области фундаментального поглощения. Типичными полупроводниками с прямозонной энергетической структурой являются GaAs, GaP, GaN, InGaAsP. К полупроводникам с непрямозонной энергетической структурой относятся германий Ge и кремний Si.

3. Форма края полосы собственного поглощения

Краем собственного поглощения называется область вблизи hω « ∆ E _g . Форма края определяется прежде всего особенностями структуры энергетических зон материала. В прямозонных полупроводниках край собственного поглощения определяется прямыми оптическими переходами, в непрямозонных — непрямыми.

Рассмотрим сначала край собственного поглощения в прямозонных полупроводниках. Коэффициент поглощения α_ω пропорционален вероятности перехода W _fj и плотности начальных (занятых) и конечных (свободных) электронных состояний, разделенных энергией hω , для которых выполняются правила отбора (6), (7). Число таких пар состояний, приходящееся на единичный интервал энергии и единицу объема кристалла, называется комбинированной плотностью состояний ( N ( hω )). Тогда

(10)

Учитывая, что уровень f расположен в С-зоне, a j — в V-зоне, можем записать:

(11)

Условие (10) позволяет рассчитывать комбинированную плотность состояний обычным методом (например, как для С-зоны). Объем сферического слоя толщиной dk равен 4π 2 k 2 dk. На одно состояние в -пространстве приходится объем (2π 3 )/ V, где V — объем кристалла. Приняв V = 1 и учитывая спиновое вырождение, получаем с учетом(11):

(12)

Вероятность перехода W _fj определяется квадратом матричного элемента , вид зависимости от k которого связан с симметрией волновых функций U _kj и U _kf. Для большинства полупроводниковых материалов симметрия U _kj и U _kf. такова, что V _fj слабо зависит от волнового вектора. Такие переходы называются разрешенными по симметрии. В этом случае можно положить V _fj = V _CV ( k = 0) = const . Тогда из (10) и (12) коэффициент поглощения для прямых разрешенных переходов

(13)

Оценка коэффициента А дает величину 10 4 см -1 • эВ 1/2 . Из (13) следует, что (α очень быстро растет с увеличением энергии фотонов при hω ≥ ∆ E _g . Очевидно, что край собственного поглощения при прямых переходах в координатах будет представлять собой прямую линию, пересекающую ось энергий в точке hω = ∆ E _g (рис. 4).

Однако при исследовании края собственного поглощения арсенида галлия было обнаружено, что экспериментальные данные существенно отличаются от теоретических как по значению коэффициента поглощения, так и по форме спектра (рис. 5). Это отличие объясняется тем, что при выводе (17) не учитывалось взаимодействие между созданными в результате поглощения электроном и дыркой. На самом деле взаимодействующие электрон и дырка образуют новую квазичастицу, называемую экситоном, которой можно приписать свою кинетическую энергию, связанную с движением центра масс, и внутреннюю энергию, обусловленную кулоновским взаимодействием. Систему электрон-дырка, являющуюся экситоном, можно считать аналогичной атому водорода. В отличие от атома водорода экситон является возбужденной неравновесной частицей. Он может исчезнуть либо в результате теплового «довозбуждения», т. е. термической диссоциации, либо вследствие аннигиляции с испусканием кванта света.

Рис. 4. Край собственного поглощения при прямых переходах

Рис. 5. Край собственного поглощения арсенида галлия, измеренный при различных температурах: 1,3— рассчитанный по формуле (13); 2, 4 — экспериментальные кривые

Из решения уравнения Шредингера для полной энергии экситона получается следующее выражение:

(14)

где К—волновой вектор экситона,

(15)

где п = 1,2. R _∞ = 13,5 эВ — постоянная Ридберга, т_о — масса свободного электрона.

Таким образом, полная энергия экситона Е состоит из его кинетической энергии , определяемой движением центра масс, и его внутренней энергии (Е _C + E _n ). Из (14) следует, что энергетический спектр экситонов содержит серию дискретных параболических зон ниже дна зоны проводимости, которые сливаются в континуум при более высоких энергиях (рис. 6). Каждая из зависимостей Е(К) с заданным п образует экситонную зону. Точка 0 есть энергия невозбужденного кристалла. Минимальная энергия ∆ E _gex = ∆ E _g — ∆ E _ex , необходимая для создания экситона, называется экситонной шириной запрещенной зоны.

Экситонные эффекты и экситонные состояния не могут быть изображены на обычных энергетических диаграммах типа рис. 2 и рис. 3, так как эти диаграммы справедливы в одноэлектронном приближении, а экситон состоит как минимум из двух частиц. Поэтому рис. 6 отличается от рис. 2 и рис. 3, в частности, по оси абсцисс отложен волновой вектор экситона, а не электрона.

Рис. 6. Экситонные энергетические зоны

Непосредственный оптический переход в экситонное состояние при поглощении фотона hω будет возможен при соблюдении закона сохранения энергии и квазиимпульса:

Поскольку hk _фот 0 и начальному состоянию отвечает точка К = 0, непосредственные оптические переходы возможны только с образованием экситона с К = 0 . Поэтому спектр собственного поглощения кристалла с учетом экситонных эффектов должен состоять из серии линий

(16)

которые переходят в непрерывный спектр при hω > ∆ E _g. Каждая из экситонных линий уширена, поэтому в реальных условиях в спектре поглощения обычно проявляется одна линия с п = 1, а линии с п > 1 накладываются друг на друга, переходя в сплошной спектр.

Коэффициент поглощения а рассчитывается по данным измерений прозрачности (коэффициента пропускания) образца. Пропусканием Т называется отношение интенсивности I _T света, прошедшего через образец, к интенсивности падающего света I ₀ . Если толщина образца d много больше длины волны λ, то связь между коэффициентом пропускания Т , коэффициентом отражения R и α выглядит следующим образом:

(17)

где п — показатель преломления материала.

В области изменения прозрачности от (1 — R )/(1 + R ) до 10% для пропускания получается более простая формула:

(18)

Когда Т R . Этого можно избежать, если измерять пропускание Т двух идентичных образцов с несколько различающимися толщинами d ₁ и d ₂. В этом случае:

(20)

Заметим, что величина D = — lg Т называется оптической плотностью образца.

В простейшем случае можно просто пренебречь изменением коэффициента отражения в узкой спектральной области вблизи края полосы поглощения.

Для определения типа оптических переходов и величины ∆ E _g необходимо построить зависимости и . Спрямление одной из этих зависимостей укажет на тип оптического перехода, а экстраполяция прямой к α = 0 даст величину ∆ E _g .

Объектами исследования в работе являются монокристаллы GaAs и Si . Образцы представляют собой пластинки, центральная часть которых протравлена до толщины 45-50 мкм у Si и 10-20 мкм у GaAs. Измерения пропускания производятся с помощью спектрофотометра СФ-26.

1. В чем состоит закон Бугера-Ламберта?

2. Каков физический смысл коэффициента поглощения?

3. Виды оптического поглощения в полупроводниках.

4. Понятие о прямозонных и непрямозонных полупроводниках.

5. Прямые переходы. Диаграмма взаимодействия и законы сохранения для прямых переходов.

6. Непрямые переходы. Диаграмма взаимодействия и законы сохранения для непрямых переходов.

7. Какое состояние называется виртуальным? Какое состояние может выступать в качестве виртуального, и чем определяется время пребывания в нем?

8. Форма края собственного поглощения при прямых переходах.

9. Что такое экситон?

10. Что собой представляет спектр экситонов?

11. Как влияют экситоны на спектр поглощения полупроводника при прямых переходах?

12. Форма края собственного поглощения при непрямых переходах.

13. Как влияют экситоны на спектр поглощения полупроводника при непрямых переходах?

14. Могут ли наблюдаться непрямые переходы в прямозонном полупроводнике?

15. Укажите область энергий фотонов, в которой обнаруживаются непрямые переходы в непрямозонном полупроводнике.

16. Какую информацию можно получить из исследований спектров собственного поглощения?

17. Как определить тип оптических переходов в полупроводнике?

18. Что такое оптическая плотность D ?

19. Если D = 1, чему равен коэффициент пропускания образца?

20. Как из измерений пропускания рассчитать коэффициент поглощения?

Измерить спектральную зависимость оптического пропускания предложенных образцов ( Si , GaAs ).

По формуле (19), используя полученные данные, рассчитать коэффициент поглощения α, считая, что коэффициент отражения постоянен и равен 0.3 для обоих материалов.

Построить зависимости и для всех образцов. Определить тип оптических переходов и ширину запрещенной зоны.

Сравнить полученные значения ∆ E _g с табличными значениями и дать интерпретацию полученных результатов.

Видео:Закон сохранения массы веществ. 8 класс.Скачать

ЛИТЕРАТУРА

Физика твердого тела. Лабораторный практикум. Под ред. Хохлова А.Ф. Изд-во Нижегородского ун-та, 2000.

Пихтин А.Н. Оптическая и квантовая электроника. Учеб.для вузов.-М.: «Высшая школа», 2001.

Шалимова К. В. Физика полупроводников. М.: Энергоатомиздат, 1985.

Уханов Ю. И. Оптические свойства полупроводников. М.: Наука, 1977.

Видео:Закон сохранения массы вещества (2)Скачать

Закон сохранения механической энергии

О чем эта статья:

Видео:Закон сохранения и превращения энергии в тепловых процессах. Практ. часть - решение задачи. 8 класс.Скачать

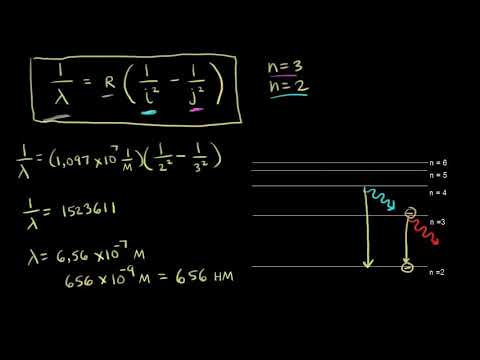
Энергия: что это такое

Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.

Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.

Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.

Видео:Спектр излучения водорода (видео 12) | Квантовая физика | ФизикаСкачать

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия

Е_к — кинетическая энергия [Дж]

m — масса тела [кг]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 кг, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 кг, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии

Ответ: гном бежал со скоростью 2 м/с.

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

Потенциальная энергия деформированной пружины

Е_п — потенциальная энергия [Дж]

k — жесткость [Н/м]

x — удлинение пружины [м]

Потенциальная энергия в поле тяжести

Е_п = mgh

Еп — потенциальная энергия [Дж]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g ≃ 9,8 м/с 2

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с 2 .

Решение:

Формула потенциальной энергии Е_п = mgh

E_п = 0,1 · 9,8 · 2500 = 2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 кг, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с 2 .

Решение:

Формула потенциальной энергии Е_п = mgh

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E₁ и E₂. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

По условию задачи

Таким образом, получим, что

Видео:Урок 455. Уравнение ШрёдингераСкачать

Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

Закон сохранения энергии

Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии

Е_{полн. мех.} — полная механическая энергия системы [Дж]

Е_п — потенциальная энергия [Дж]

Е_к — кинетическая энергия [Дж]

const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Е_п = 0. В этот же момент времени Е_к максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v₀, поднялось на максимальную высоту h₀. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Е_мех = Е_п = mgh₀.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Е_мех = mgh₀.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

m = 100 г = 0,1 кг

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Видео:Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать

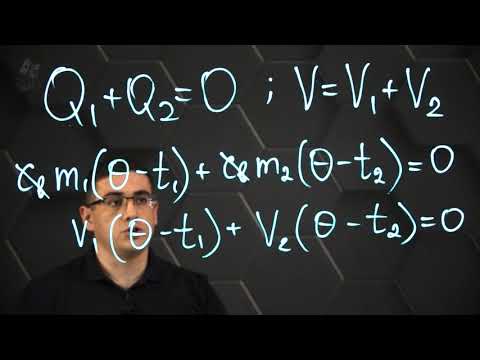
Переход механической энергии во внутреннюю

Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.

Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.

Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.

Задачка

Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?

Решение:

В самом начале у мяча есть только кинетическая энергия, то есть Е_мех = Е_к.

В конце механическая энергия равна половине начальной, то есть Е_мех/2 = Е_к/2

Часть энергии уходит во внутреннюю, значит Е_полн = Е_мех/2 + Е_внутр

Ответ: во внутреннюю перейдет половина начальной кинетической энергии

Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

Закон сохранения энергии в тепловых процессах

Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.

Вот что сформулировал Фурье:

При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.

Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.

Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.

Закон сохранения энергии в тепловых процессах

При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.

Математически его можно описать так:

Уравнение теплового баланса

Q_отд — отданное системой количество теплоты [Дж]

Q_пол — полученное системой количество теплоты [Дж]

Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:

Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.

Чтобы разобраться в задачках, читайте нашу статью про агрегатные состояния вещества.

Задачка раз

Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.

Удельная теплота сгорания спирта 2,9 · 10₇ Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг · °С).

Решение:

При нагревании тело получает количество теплоты

где c — удельная теплоемкость вещества

При сгорании тела выделяется энергия

где q — удельная теплота сгорания топлива

По условию задачи нам известно, что на нагревание воды пошло 20% энергии, полученной при горении спирта.

Ответ: масса сгоревшего топлива равна 33,6 г.

Задачка два

Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг · ℃, удельная теплота плавления льда равна 3,3 · 10 5 Дж/кг.

Решение:

Для нагревания льда до температуры плавления необходимо:

Q_нагрев = 2100 · 0,5 · (10 − 0) = 10 500 Дж

Для превращения льда в воду:

Q_пл = 3,3 · 10 5 · 0,5 = 165 000 Дж

Таким образом, для превращения необходимо затратить:

Q = Q_нагрев + Q_пл = 10 500 + 165 000 = 175 500 Дж = 175,5 кДж

Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.