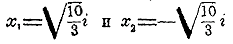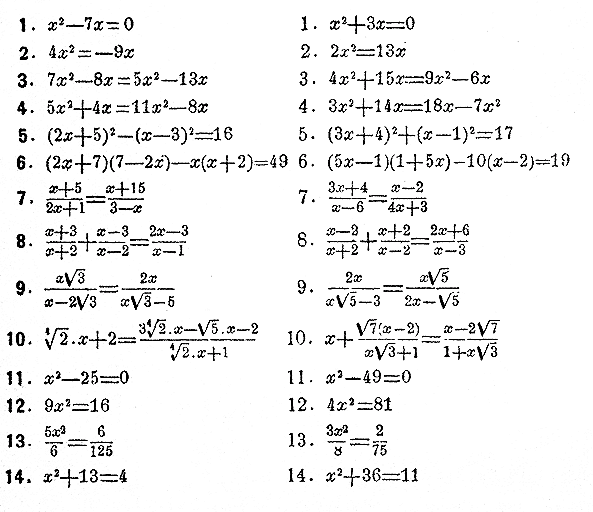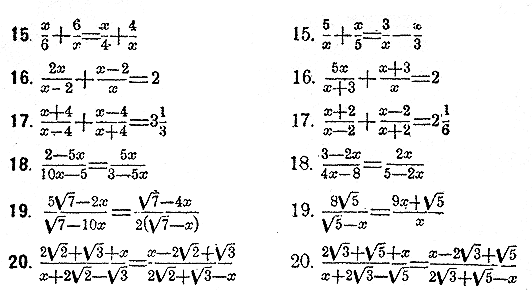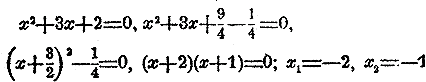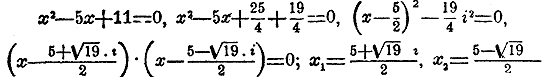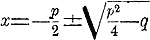Уравнение во второй степени как решать

УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ.

§ 1. Рeшeниe числовых уравнeний второй стeпени.

Уравнeнием второй степени или квадратным уравнением называeтся всякоe уравнениe, котороe посрeдством прeобразований, замeняющих его другими, совмeстными с ним уравнeниями, можeт быть привeдeно к виду ax 2 + bx + c = 0.

Послeднеe уравнeниe называeтся о б щ и м видом квадратных уравнeний. Количeства а, b и с называются коэффициентамн уравнения. Если эти коэффициeнты выражeны дробными количeствами, то их можно замeнить цeлыми количeствами. Коэффициент а всегда можно считать положитeлным. Если случайно коэффициeнт с равен нулю или b равeн нулю, то получаeтся так называемоe нeполноe квадратноe уравнение. Рeшить квадратноe уравнениe значит найти тe значeния х которые обращают данноe ураваениe в тождeство. Таких значeний или корнeй всякоe квадратноe уравнeниe имeет два.

Для рeшения нeполного уравнeния ax 2 + bx = 0 достаточно вывести в первой части eго за скобки х. Получится х(ax + b)= 0. Из этого видно, что уравнению можно удовлeтворить двумя способами: или полагая х = 0, отчeго обращаeтся в нуль первый множитель пeрвой части уравнения, или полагая х = — b /_a, отчeго обращается в нуль второй множитель. В обоих этих случаях всe произвeдeниe будет равно второй части уравнeния, т.e. равно нулю, и, слeдоватeльно, уравнениe будет удовлeтворeно.

Рассматривая второe неполноe уравнeниe ax 2 + с = 0, различим два сдучая, когда коэффициeят с отрицатeлeн и когда он положителeн. Положим, напр., что дано уравнeниe 4x 2 —7 = 0 . Рассматривая первую часть, как разность квадратов, можно разложить ее в произведениe. Получим (2х—√ 7 )(2х+√ 7 )= 0. Но произведение может быть равно нулю только тогда, когда один из множителей равен нулю. Поэтому данное уравнениe совмe-щает в себe два корня, удовлeтворяющиe порознь двум уравнениям первой степени 2х—√ 7 = 0 и 2х+√ 7 = 0. Значит корни его суть x₁ = √ 7 /₂ и x₂ = — √ 7 /₂

Положим тепeрь, что дано уравнeние 3x 2 + 10 = 0. Пeрвая часть eго может быть разложена в произведениe посредством мнимых количеств. Дeйствительно, так как i 2 = —1, то можно написать данноe уравнениe в видe 3x 2 — 10i 2 = 0 . Послe этого, рассматривая первую часть, как разность квадратов, имeем (√ 3 • х —√ 10 • i)(√ 3 • х + √ 10 • i) = 0, откуда видно, что данноe уравнение разлагается на два

и потому имeeт два мнимых корня

Рeшить нeполные квадратные уравнения:

Решение полного квадратного уравления ax 2 + bx + c = 0 состоит такжe в разложении первой части eго на множители. Это преобразовавие значительно упрощаeтся в том случаe, когда коэффициент при высшем членe есть единица. Замeтим, что всякоe квадратноe уравнeнио можно привести к такому виду. Нужно только раздeлить обe части на коэффициeпт а, Получим x 2 + b /_a x + с /_a = 0 Обыкновенно обозначают b /_a буквой р и с /_a буквой q, отчего уравнeниe пишeтся в видe x 2 + px + q = 0. Такой вид уравнения называeтся приведeнным. Неудобно, однако, так преобразовывать всякое уравнениe к привeдeнному виду, потому что в послeднем коэффициенты р и q часто оказываются дробными.

Рассмотрим частные виды уравнений с цeлыми коэффициентами.

Дано уравнeние x 2 — 8x + 15 = 0. В пeрвой части настоящаго сборника указывался способ для разложения трехчленов второй степени в произвeдениe. Этот способ слeдует припомнить и примeнять, гдe удобно, в нижеслeдующих задачах.

Укажем теперь другой способ, болeе сложный, но и болee общий, состоящий в прeобразовании трeхлена к виду разности квадратов. Принимая x 2 за квадрат и 8x за удвоeнноe произведение, легко видeть, что для преобразовяния x 2 — 8x к виду полного квадрата нужно прибавить ещe второй квадрат 16. Прибавляя это число к первой части данного уравнeния и затeм вычитая то жe число из нее, представим уравнение в видe x 2 — 8x + +16 — 1 = 0 или в видe (х— 4) 2 —1=0. Послe этого пeрвая часть легко разлагается в произведение,именно получаем(х— 3)(х— 5)=0 и находим два корня уравнения
x₁ = 3 и x₂ =5.

Иногда, подобное разложeние трехчлена требует ввeдeния мнимых количеств. Так, если дано уравлениe x 2 + 2x + 7 = 0 , то, преобразовав первые два члена его к виду полного квадрата, находим x 2 + 2x + 1 + 6 = 0 или (х+ 1) 2 + 6=0. Но в первой части получается теперь не разность, а сумма. Заметив, что i 2 = —1, пишем уравнение в виде
(х+ 1) 2 — 6i 2 = 0, затем разлагаем в форму (х+ 1—√ 6 • i)(х+ 1+√ 6 • i)=0 и наконец нахо-дим два мнимых корня x₁ = —1+ √ 6 • i и x ₂= —1— √ 6 • i

Если коэффициент члена, содержащего х в первой степени, есть нечетное число, то действие усложняется тем, что для составления полного квадрата нужно вводить новый квадрат от дробного числа. Напр., имеем:

Решить полные квадратные уравнения:

Так как приходится решать квадратные уравнения очень часто, то неудобно в каждом отдельном случае проделывать те преобразования, посредством которых квадратное уравнение разлагается на два уравнения первой степени. Квадратные уравнения решают по общей формуле. В курсах алгебры доказывается, что, если уравнение имеет вид
ax 2 + bx + c = 0, то корни выражаются формулой

, т.-е. корень общего квадратного уравнения равен среднему коэффициенту взятому с противоположным знаком, плюс или минус квадратный корень из разности между квадратом среднего коэффициента и учетверенным произведением крайних коэффициентов, все деленное на удвоенный первый коэффициент.

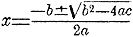
Кроме этой формулы нужно знать еще более простую формулу, соответствующую тому случаю, когда средний коэффициент есть четное число. Если уравнение имеет вид
αx 2 + 2βx + c = 0, то 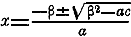, т.е. корень квадратнаго уравнения с четным средним коэффициентом равен половине среднего коэффициента, взятой с противоположным знаком, плюс или минус квадратный корень из разности между квадратом этой половины и произведением крайних коэффициентов, все деленное на первый коэффициент.

Наконец, еще полезно заметить наиболее простую формулу, соответствующую тому случаю, когда первый коэффициент есть единица, а средний четное число. Если уравнение имеет вид x 2 + 2βx + c = 0, то х = —β ±√ β 2 —с , т.е. корень приведенного квадратного уравнения с четным средним коэффициентом равен половине второго коэффициента, взятой с противоположным знаком, плюс или минус квадратный корень из разности между квадратом этой половины и третьим коэффициентом.

Каждую из указанных формул нужно прилагать не прежде, как преобразовав уравнение к простейшему виду, в котором все коэффициенты суть целые количества и первый коэффициент положителен. Нужно помнить притом, что коэффициенты рассматриваются вместе со знаками их.

Примечание. В курсах алгебры указывается еще формула . Если уравнение имеет вид
x 2 + px + q = 0, то

Эта формула есть общая , потому что всякое квадратное уравнение может быть преобразовано в приведенное. Но для вычисления корнeй упомянутая формула неудобна, потому что приводит дeйствиe с цeлыми количествами к дeйствию с дробями.

При начальных упражнениях полeзно выписывать коэффициeнты с их знаками отдeльно от буквы, обозначающeй нeизвeстное. Для первых упражнений слeдуeт пeрeдeлать вновь примeры с 21 до 40, ужe приведенные выше.

Преобразовать к простeйшему виду и рeшить уравнeния:

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнение во второй степени как решать

Для решения уравнения второй степени необходимо переписать его в такой вид, чтобы на первом месте стояло число, которое умножается на х 2 , дальше было число, которое умножается на х и на третьем месте — просто свободное число. При этом все выражение должно быть равно 0.

Другими словами, мы должны привести наше уравнение к виду

где a, b, c — любые числа.

Распространенной ошибкой является то, что начинают решать по невнимательности, не обратив внимание на правую часть. Например уравнение

Нельзя начинать решать, пока все числа не будут перенесены в левую часть и не будут приведены подобные.

Решаемым уравнением будет в данном случае уравнение

Дальше, вычисляем дискриминант. Он рассчитывается по формуле

Определив дискриминант, мы можем определить корни уравнения. Корней будет два

Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Уравнения второй степени: формулы, как их решать, примеры, упражнения

Уравнения второй степени: формулы, как их решать, примеры, упражнения — Наука

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Содержание:

В квадратные или квадратные уравнения и неизвестное имеют видтопор 2 + bx + c = 0.Где a ≠ 0, поскольку если бы он был равен 0, уравнение было бы преобразовано в линейное уравнение, а коэффициенты a, b и c — действительные числа.

Неизвестным, которое предстоит определить, является значение x. Например, уравнение 3x 2 — 5x + 2 = 0 — полное квадратное уравнение.

Существуют также варианты, известные как неполные уравнения второй степени, в которых отсутствуют какие-либо члены, кроме топор 2 . Вот некоторые примеры:

Аль-Джуарисми, известный арабский математик античности, описал в своих работах различные типы уравнений первой и второй степени, но только с положительными коэффициентами. Однако именно французский математик Франсуа Вите первым ввел буквы для обозначения величин и предложил решение с помощью формулы решительный:

Это общая формула, позволяющая решить квадратное уравнение, найти его корни или нули, даже если решения не являются действительными. Есть и другие способы их решения.

Видео:Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать

Как решать квадратные уравнения?

Уравнения второй степени могут быть решены с использованием формулы, приведенной выше, и есть также другие алгебраические процедуры, которые могут дать результаты в некоторых уравнениях.

Мы собираемся решить уравнение, предложенное в начале, с формулой, подходящим методом для любого квадратного уравнения с одной неизвестной:

Чтобы правильно использовать формулу, обратите внимание, что:

• к коэффициент при члене с x 2
• б коэффициент при линейном члене
• c это самостоятельный термин.

Мы собираемся идентифицировать их с помощью того же уравнения:

Обратите внимание, что знак, который сопровождает коэффициент, необходимо учитывать. Теперь подставляем эти значения в формулу:

В числителе стоит символ «плюс — минус» ±, который указывает, что величина с корнем может приниматься как положительная, так и отрицательная. Квадратное уравнение имеет не более двух действительных решений, и этот символ учитывает это.

Позвоните x₁ и х₂ к этим двум решениям, то:

Икс₂ = (5-1) / 6 = 4/6 = 2/3

Видео:Решение систем уравнений второй степениСкачать

Разрешение по факторингу

Некоторые уравнения второй степени состоят из трехчленов, которые легко разложить на множители. Если так, то этот метод работает намного быстрее. Рассмотрим уравнение:

Икс 2 + 7x — 18 = 0

Факторизация имеет следующий вид:

Пустые места заполняются двумя числами, которые при умножении дают 18, а при вычитании — 7. Знаки в скобках выбираются по этому критерию:

-В первой скобке знак ставится между первым и вторым слагаемыми.

-А во второй скобке указано произведение увиденных знаков.

Что касается чисел, то в этом случае их легко подсчитать: это 9 и 2. Самый большой всегда помещается в первую из круглых скобок, например:

Икс 2 + 7x — 18 = (x + 9). (х — 2)

Читатель может проверить с помощью свойства дистрибутивности, что при построении произведения правой части равенства получается трехчлен левой. Теперь уравнение переписано:

Для выполнения равенства достаточно, чтобы один из двух множителей был равен нулю. Итак, в первом x должно быть выполнено₁ = -9 или может оказаться, что второй множитель исчезнет, ​​и в этом случае x₂ = 2. Это решения уравнения.

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Графический метод

Корни или решения квадратного уравнения соответствуют пересечениям параболы y = топор 2 + bx + c с горизонтальной осью или осью x. Таким образом, при построении графика соответствующей параболы мы найдем решение квадратного уравнения, сделав y = 0.

Разрезы параболы с горизонтальной осью представляют собой решения уравнения топор 2 + bx + c = 0. Парабола, которая пересекает горизонтальную ось только в одной точке, имеет единственный корень, и он всегда будет вершиной параболы.

И наконец, если парабола не пересекает горизонтальную ось, соответствующее уравнениетопор 2 + bx + c = 0 ему не хватает реальных решений.

Построение графика вручную может быть трудоемким, но с использованием онлайн-программ для построения графиков это очень просто.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Разрешение научного калькулятора

Многие модели научных калькуляторов позволяют решать квадратные уравнения (а также уравнения других типов). Чтобы узнать это, вам нужно проверить меню.

После выбора варианта квадратного уравнения для одного неизвестного, меню просит ввести значения коэффициентов a, b и c и возвращает реальные решения, если они существуют. И есть также модели научных калькуляторов, которые работают с комплексными числами и предлагают эти решения.

Видео:Алгебра 9 класс (Урок№25 - Решение систем уравнений второй степени.)Скачать

Дискриминант квадратного уравнения

Чтобы узнать, имеет ли уравнение действительные решения или нет и сколько их, без необходимости сначала решать, дискриминант Δ определяется как величина под квадратным корнем:

По знаку дискриминанта известно, сколько решений имеет уравнение по этому критерию:

-Два реальных решения: Δ> 0

-Реальное решение (или два одинаковых решения): Δ = 0

-Нет реального решения: Δ 2 + 12x + 64 = 0? Идентифицируем коэффициенты:

Δ = Ь 2 — 4ac = 12 2 — 4x (-7) x 64 = 144 + 1792 = 1936> 0

У уравнения есть два решения. Теперь посмотрим на этот другой:

Икс 2 — 6x + 9 = 0

Δ = (-6) 2 — 4 х 1 х 9 = 36 — 36 = 0

Это уравнение с одним решением или с двумя равными решениями.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Примеры простых квадратных уравнений

Вначале мы сказали, что уравнения второй степени могут быть полными, если трехчлен есть, и неполными, если линейный член или независимый член отсутствует. Теперь давайте посмотрим на некоторые конкретные типы:

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Уравнение вида x 2 + mx + n = 0

В этом случае a = 1 и формула сводится к:

Для этого типа уравнения и всегда в зависимости от оставшихся коэффициентов, метод факторизации может работать хорошо, как мы видели в предыдущем разделе.

Видео:ВСЕ РЕАКЦИИ С АЗОТОМ И ЕГО СОЕДИНЕНИЯМИ | ЕГЭ ХИМИЯ 2024| НООСкачать

Неполное уравнение вида ax 2 + c = 0

Решение, если оно существует, имеет вид:

Когда a или c имеют отрицательный знак, существует реальное решение, но если два члена имеют одинаковый знак, решение будет мнимым.

Видео:Решение задач с помощью систем уравнений второй степени. Урок 17. Алгебра 9 классСкачать

Неполное уравнение вида ax 2 + bx = 0

Это уравнение быстро решается с использованием факторизации, поскольку x является общим множителем в обоих терминах. Одно из решений всегда x = 0, другое находится так:

ах + Ь = 0 → х = -b / а

Давайте посмотрим на пример ниже. Решить:

Следовательно, x₁ = 0 и x₂ = 5

Видео:ЛОВИ ПРОДОЛЖЕНИЕ 😉 ДИСКРИМИНАТ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать

Уравнения со знаменателем

Существуют различные уравнения рационального типа, в которых неизвестное может присутствовать как в числителе, так и в знаменателе или даже только в последнем, и которые с помощью алгебраических манипуляций сводятся к квадратным уравнениям.

Чтобы решить их, нужно умножить обе части равенства на наименьшее общее кратное или m.c.m знаменателей, а затем переставить члены. Например:

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Уравнения высшего порядка, которые становятся квадратичными

Существуют уравнения более высокого порядка, которые можно решить, как если бы они были квадратичными, с помощью замены переменной, например это уравнение двуквадратный:

Икс 4 — 10x 2 + 9 = 0

Пусть x 2 = u, тогда уравнение принимает вид:

или 2 — 10u + 9 = 0

Это уравнение быстро решается путем факторизации, нахождения двух чисел, которые умножаются на 9 и складываются с 10. Это числа 9 и 1:

Следовательно, решениями этого уравнения являются u₁ = 9 и u₂ = 1. Теперь возвращаем изменение:

Икс 2 = 9 → х₁ = 3 и x₂ = -3

Икс 2 = 1 → х₁ = 1 и x₂ = -1

Исходное уравнение имеет порядок 4, поэтому у него не менее 4 корней. В примере это -3, -1, 1 и 3.

Видео:МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ II #математика #егэ #shorts #профильныйегэСкачать

Простые решаемые упражнения

Видео:СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

— Упражнение 1

Решите следующее квадратное уравнение с неизвестным в знаменателе:

Наименьшее общее кратное — это x (x + 2), и вы должны умножить все члены:

Эквивалентное выражение остается:

5х (х + 2) — х = х (х + 2)

5x 2 + 10х — х = х 2 + 2x

Все слагаемые переносим слева от равенства, а справа оставляем 0:

5x 2 + 10х — х — х 2 — 2x = 0

Мы учитываем, поскольку это неполное уравнение:

Одно из решений x = 0, другое:

Видео:СИСТЕМА УРАВНЕНИЙ второй степени 8 классСкачать

— Упражнение 2.

Найдите решение квадратных уравнений:

а) -7x 2 + 12x + 64 = 0

б) х 2 — 6x + 9 = 0

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Решение для

Из этого уравнения мы знаем определитель Δ, потому что он был вычислен в качестве примера ранее, поэтому мы собираемся воспользоваться им, выразив разрешающую формулу следующим образом:

Икс₁ = (-12+44) / -14 = – (32/14) = – (16/7)

Икс₂ = (-12 – 44) / -14 = 4

Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Решение б

Квадратный трехчлен x 2 — 6x + 9 факторизуем, так как это трехчлен полного квадрата:

Икс 2 — 6х + 9 = (х-3) 2 = 0

Решение этого уравнения — x = 3.

Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

— Упражнение 3.

Какое уравнение имеет решения 3 и 4?

Решение

Применение распределительного свойства:

Икс 2 — 4х -3х + 12 = 0

Два центральных члена похожи и могут быть сокращены, в результате чего остается:

Икс 2 — 7х + 12 = 0

Ссылки

1. Балдор. 1977. Элементарная алгебра. Венесуэльские культурные издания.
2. Хоффман, Дж. Выбор тем по математике. Том 2.
3. Хименес, Р. 2008. Алгебра. Прентис Холл.
4. Стюарт, Дж. 2006. Precalculus: математика для исчисления. 5-е. Издание. Cengage Learning.
5. Сапата, Ф. 4 способа решения квадратного уравнения. Получено с: francesphysics.blogspot.com.
6. Зилл, Д. 1984. Алгебра и тригонометрия. Макгроу Хилл.

Неверность: причины и последствия

Бересклет японский: характеристика, среда обитания, свойства, уход