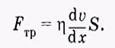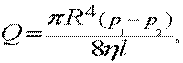Уравнение внутреннего трения вязкости уравнение ньютона (3 видео)

Вязкость жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости. Формула Пуазейля.

При течении реальной жидкости отдельные слои ее воздействуют друг на друга ссилами, касательными к слоям. Это явление называют внутренним трением или вязкостью.

dv/dx – производная, называемая градиентом скорости.

S– площадь взаимодействующих слоев
Это уравнение Ньютона. Сила внутреннего трения , действующая между слоями жилкости площадью S.ŋ— коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью (или просто вязкостью). Вязкость зависит от состояния и молекулярных свойств жидкости (или газа).

du/dx — градиента скорости (скорости сдвига)
Единицей вязкости является паскалъ-секунда (Па • с). В системе СГС вязкость выражают в пуазах (П): 1 Па • с = 10 П.

Ньютоновские и неньютоновские жидкости. Кровь как неньютоновская жидкость.
Ньютоновские жидкости – жидкости, вязкость которых не зависит от градиента скорости(т.е.вязкость постоянна).Это все низкомолекулярные в-ва в жидком состоянии, их смеси и истинные растворы в них низкомолекулярных в-в (вода, органич. жидкости, расплавл. металлы, соли и стекло при темп-ре выше темп-ры размягчения). Такие жидкости подчиняются уравнению Ньютона.
Коэффициент пропорциональности η (греческая буква «эта») называют коэффициентом внутреннего трения или динамической вязкостью. Единицей динамической вязкости (или просто вязкости) в системе СИ является

Неньютоновские жидкости – вязкость которых зависит от градиента скорости (т.е.вязкость не постоянная) Они не подчиняются уравнению Ньютона. Это жидкости, состоящие из крупных и сложных молекул, например эмульсии, суспензии, пены и кровь. Такие жидкости содержат молекулы или частицы, склонные к образованию пространственных структур.
Цельная кровь (суспензия эритроцитов в белковом растворе – плазме крови) в отличие от плазмы крови является неньютоновской жидкостью. Вязкость крови уменьшается с увеличением скорости v (или градиента скорости dv/dx) течения крови. Связано это с тем, что в неподвижной крови или при малых скоростях ее течения эритроциты склонны к агрегации (слипанию) и образуют структуры, напоминающие столбики монет («монетные столбики»), что приводит к возрастанию вязкости. При увеличении скорости движения крови «монетные столбики» разрушаются, и вязкость крови снижается. При остановке движения крови, эритроциты быстро (примерно, за 1 с) вновь собираются в «монетные столбики».

Закон Пуазейля (математическим выражением которого является формула Пуазейля) устанавливает зависимость между объемом жидкости, протекающим через трубу в единицу времени (расходом), длиной и радиусом трубы, и перепадом давления в ней

Q – объемная скорость, R – радиус сосуда,  – динамическая вязкость, l – длина сосуда, p₁  p₂ – разность давлений на концах сосуда.

Вопрос 10

Методы определения вязкости крови: капиллярные, ротационные. Закон Стокса . Диагностическое значение вязкости крови

Закон Стокса

Совокупность методов измерения вязкости называют вискозиметрией, а приборы, используемые для таких целей, — вискозиметрами.

Капиллярный метод основан на формуле Пуазейля и заключается в измерении времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном’ перепаде давлений. Капиллярный вискозиметр применяется для определения вязкости.Капиллярными вискозиметрами измеряют вязкость от значений 10 -5 Па • с, свойственных газам, до значений 10 4 Па • с, характерных для консистентных смазок.
Применяются также ротационные вискозиметры, в которых жидкость находится в зазоре между двумя соосными телами, например цилиндрами. Один из цилиндров (ротор) вращается, а другой неподвижен. Вязкость измеряется по угловой скорости ротора, создающего определенный момент силы на неподвижном цилиндре, или по моменту силы, действующему на неподвижный цилиндр, при заданной угловой скорости вращения ротора.С помощью ротационных вискозиметров определяют вязкость жидкостей в интервале 1—10 5 Па • с, т. е. смазочных масел, расплавленных силикатов и металлов, высоковязких лаков и клеев, глинистых растворов и т. п.В ротационных вискозиметрах можно менять градиент скорости, задавая разные угловые скорости вращения ротора. Это позволяет измерять вязкость при разных градиентах и установить зависимость η = f(dv/dx), которая характерна для неньютоновских жидкостей.
В настоящее время в клинике для определения вязкости крови используют вискозиметр Гесса с двумя капиллярами
В вискозиметре Гесса объем крови всегда одинаков, а объем воды отсчитывают по делениям на трубке 1, поэтому непосредственно получают значение относительной вязкости крови. Для удобства втсчета сечения трубок 1 и 2 делают различными так, что, несмотря на разные объемы крови и воды, их уровни в трубках будут примерно одинаковы.
Вязкость крови человека в норме 4—5 мПа • спри патологии колеблется от 1,7 до 22,9 мПа * с, что сказывается на скорости оседания эритроцитов (СОЭ). Венозная кровь обладает несколько большей вязкостью, чем артериальная. При тяжелой физической работе увеличивается вязкость крови. Некоторые инфекционные заболевания увеличивают вязкость крови, другие же, например брюшной тиф и туберкулез, — уменьшают.

Видео:Три Закона Ньютона. Простое ОбъяснениеСкачать

Вязкость жидкости. Закон Ньютона. Ньютоновские и неньютоновские жидкости.

Основные величины, характеризующие движение жидкости или газа. Линейная и объёмная скорости; соотношение между ними.

Основной характеристикой любого движения является его скорость. В случае течения жидкости (или газа) термин „скорость“ применяется в двух смыслах. Скорость перемещения самих частиц жидкости(или плывущих вместе с жидкостью мелких тел – например, эритроцитов в крови)обозначают υ и называют линейной скоростью. м/с , где х – координата частицы (при равномерном движении можно написать ). Однако, на практике чаще важнее знать объём V жидкости, протекающей в данном потоке(в трубе, в русле реки, в кровеносном сосуде и т.п.) за единицу времени.Эту величину называют объёмной скоростью и обозначают Q.

Q = . (1)

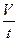
Между линейной скоростью υ и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S (см. рисунок 1).

Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1. Через некоторое время t он переместится в положение 2, отстоящее на расстояние x = υ·t . При этом через трубку пройдёт объём жидкости V = S·x . Объёмная скорость жидкости Q при этом будет равна 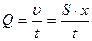. Но , поэтому

Если течение стационарно, то

Это уравнение неразрывности струи.

Течение идеальной жидкости. Теорема Бернулли.

Идеальная жидкость – жидкость несжимаемая и неимеющая силы внутреннего трения. Следовательно при движении жидкости не происходит диссипации энергии, ее полная энергия постоянна. Если жидкость движется под действием внешнего давления, то ее полная энергия есть сумма кинетической энергии, потенциальной энергии ,силы тяжести и потенциальной энергии давления. . Для идеальной жидкости Е= const. . Разделим на объем жидкости V, так как жидкость несжимаема, V = const.

, — плотность жидкости.

уравнение (теорема) Бернулли.

р – внешнее статическое давление, которое, согласно закона Паскаля, передается жидкостью во все стороны без изменения. давление силы тяжести жидкости или гидростатическое давление. — давление, создаваемое вследствие движения жидкости -–динамическое давление, направленное по вектору скорости жидкости. Для горизонтального течения жидкости, когда =const, можно уравнение Бернулли упростить: .

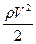
При нормальном кровообращении, как нетрудно подсчитать, динамическое давление составляет всего 1% 3% от полного. Например, в аорте линейная скорость крови около 0,7 метра в секунду, откуда

(плотность крови ≈ 1000 кг.м –3 ). Полное давление крови в аорте (среднее) около 120 мм.рт.столба. Учитывая, что 1 мм.рт.ст. = 133 паскаля, получаем, что полное давление равно 16.10 3 Па, то есть р_{динамич} ≈ 1,5%. Однако, при усиленной физической нагрузке, а также при некоторых заболеваниях динамическое давление заметно возрастает, и его необходимо учитывать.

Вязкость жидкости. Закон Ньютона. Ньютоновские и неньютоновские жидкости.

В реальных жидкостях всегда существуют силы трения. Причины трения – межмолекулярные взимодействия. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трениемили вязкостью (эти термины являются синонимами).

Рассмотрим два слоя жидкости, движущиеся с разными скоростями (рис. 5). Расстояние между слоями равно х.

SSs v ₁

Х S v ₂

Уравнение внутреннего трения вязкости уравнение ньютона

Выделим в каждом слое площадку с площадью S. Ньютон показал, что сила трения между этими слоями равна:

(6)

(знак „минус“ показывает, что сила трения направлена навстречу движению). Эта формула носит название формула Ньютона.

Коэффициент η (эта) называется коэффициент вязкости или просто вязкость (реже говорят „коэффициент внутреннеготрения“). F = — η grad S Размерность величины η есть Па.с;

Ньютоновские и неньютоновские жидкости

Для большинства жидкостей коэффициент вязкости η при постоянной температуре есть постоянная величина, зависящая только от природы жидкости и не зависящая от её скорости (точнее, от градиента скорости; см. формулу «8»). Такие жидкости принято называть „ньютоновскими“, то есть строго подчиняющимися закону Ньютона.

Однако, опыт показал, что для ряда жидкостей η ≠ const. При малых градиентах скорости(что чаще всего бывает, когда сама скорость движения жидкости мала) вязкость относительно велика, но с ростом градиента скорости вязкость уменьшается,приближаясь к некоторому, сравнительно малому постоянному значению η_0.

Такие жидкости называются „неньютоновскими“ К ним относятся, во-первых, растворы веществ, молекулы которых в растворе образуют достаточно сильные межмолекулярные связи. Эти связи затрудняют перескоки молекул из одного положения в другое и тем самым снижают текучесть раствора, то есть увеличивают его вязкость. Плазма крови содержит большое количество растворённых белков, и в ней плавает большое число клеток (в основном – эритроцитов); кровь – это типичная неньютоновская жидкость. Поэтому, в частности, в капиллярах, где скорость течения крови мала, вязкость крови заметно больше, чем в крупных сосудах; это необходимо учитывать при расчётах движения крови в системе кровообращения.

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Вязкость (внутреннее трение). Закон Ньютона. Коэффициент вязкости

Вязкость (внутреннее трение) связано с возникновением сил трения между слоями газа (жидкости), перемешивающимися друг с другом с различными по модулю скоростями.

Со стороны слоя движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила и наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа (жидкости). Силы трения которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев. С молекулярно-кинетической точки зрения причиной вязкости является упорядоченное движение слоев с различными скоростями u и хаотичного движения молекул υ.

Согласно закону Ньютона сила трения между двумя слоями газа или жидкости равна.

Эмпирическое уравнение вязкости, закон Ньютона:

где η – коэффициент вязкости; — величина показывающая, как быстро изменяется

скорость течения жидкости или газа в направлении z, перпендикулярном к направлению движения слоев (градиент скорости u), S – площадь лежащей на границе между слоями поверхности, по которой действует сила F.

Согласно 2-му закону Ньютона:

или, , тогда

Уравнение Ньютона для внутреннего трения можно представить в виде:

где Δр_им – импульс, передаваемый от слоя к слою за секунду (Δt=1 с), т.е. поток импульса через поверхность S. Знак «минус» в формуле обусловлен тем, что импульс «течет» в направлении убывания скорости u. Поэтому знаки импульса и градиента скорости u противоположны.

В формуле Ньютона минус писать нельзя, потому что она определяет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга. Кроме того нужно брать модуль градиента скорости, так как производная может иметь любой знак, а модуль силы – положительная величина.

Рассмотрим происхождение силы внутреннего трения.

Рассмотрим два соприкасающихся слоя газа толщиной Δz. Слои движутся с различными скоростями u₁ и u₂. Каждая молекула газа участвует в двух движениях: хаотическом тепловом, средняя скорость которого равна , и упорядоченном движении со скоростью потока u. Скорость потока намного меньше, чем скорость теплового движения. В неподвижном газе средний импульс молекулы равен нулю. Молекула в потоке газа обладает средним импульсом mu. При рассмотрении внутреннего трениянас будет интересовать этот импульс.

Пусть в некоторый момент времени слои обладают импульсами р_им1 и р_им2. При отсутствии внешнего воздействия на слои, их импульсы не могут оставаться неизменными, так как вследствие теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она отдает избыток своего импульса другим молекулам ( если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее, убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила, тормозящая его движение, а к слою, скорость которого меньшая, — такая же по модулю сила, ускоряющая его движение. Таков механизм возникновения сил внутреннего трения.

Через поверхность S, лежащую на границе раздела слоев, переходит в единицу времени из одного слоя в другой количество молекул, определяемое выражением:

на среднюю скорость молекул в направлении, перпендикулярном к слоям, движение слоев со скоростью u не оказывает влияния). В результате возникает в направлении от более быстрого слоя к более медленному поток импульса через поверхность S, равный:

В реальном потоке газа скорость при переходе через воображаемую границу двух слоев изменяется не скачком, а непрерывно по закону u=u(z). Будем считать, что каждая молекула, пролетающая через поверхность S, несет с собой импульс mu, определяемый скоростью u в том месте, где произошло столкновение молекулы. Это столкновение происходит на различных расстояниях от S. В среднем последнее столкновение происходит на расстоянии, равном длине свободного пробега λ. Поэтому молекулам, летящим в направлении оси z, припишем значение скорости u₁=u(z–λ), а молекулам, летящим в противоположном направлении, – значение скорости u₂=u(z+λ). Подстановка этих значений в формулу для потока импульса через поверхность S в направлении оси z дает выражение: