Уравнение винтовой линии на цилиндре (5 видео)

Уравнение винтовой линии на цилиндре

Линии в пространстве

Винтовая линия (рис. 7.20)

Винтовая линия — линия, описываемая точкой M, которая вращается с постоянной угловой скоростью w вокруг неподвижной оси (Oz) и одновременно перемещается поступательно с постоянной скоростью v вдоль этой оси.

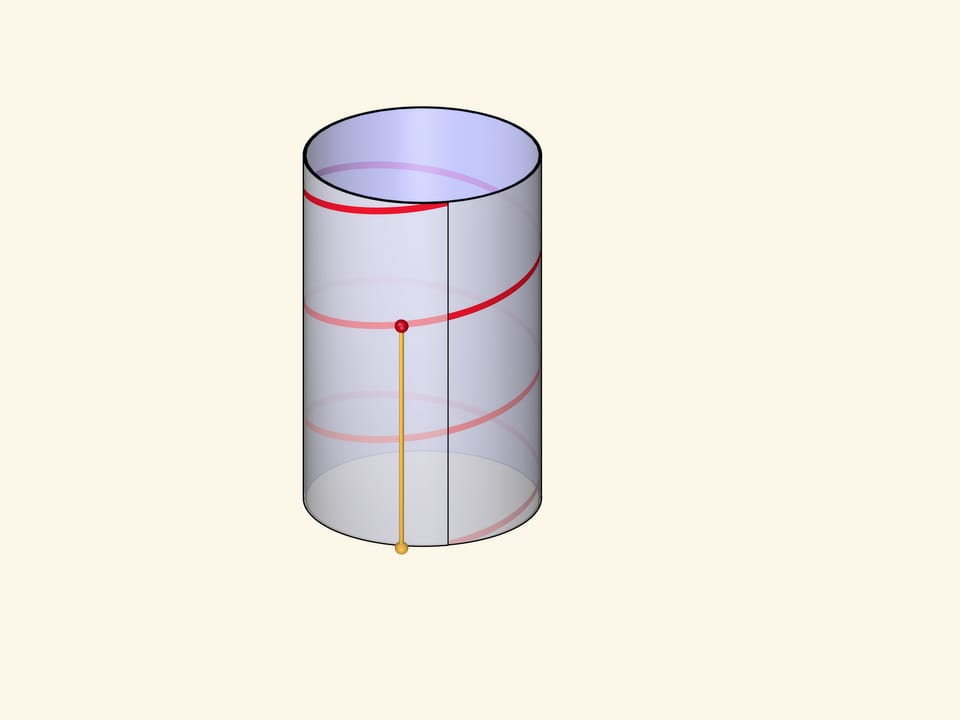
где a — радиус цилиндра, на котором расположена линия; — шаг винтовой линии.

Проекции винтовой линии на координатные плоскости:

на плоскость xOy:

— окружность;

на плоскость yOz:

— синусоида;

на плоскость xOz:

— синусоида.

Длина винтовой линии от точки пересечения с плоскостью xOy до произвольной точки

Параметрические уравнения винтовой линии, где за параметр принята длина дуги:

Кривизна:

Кручение:

Видео:Видеоурок по математике "Цилиндр"Скачать

Цилиндрические винтовые линии

По этой ссылке вы найдёте полный курс лекций по математике:

Цилиндрическая винтовая линия представляет собой пространственную кривую линию одинакового уклона. Острие резца, соприкасаясь с поверхностью равномерно вращающегося цилиндрического стержня, оставляет на нем след в виде окружности. Если же при этом сообщить резцу равномерное поступательное движение вдоль оси цилиндра, то на поверхности цилиндра получится цилиндрическая винтовая линия.

На рисунке 218 показано образование винтовой линии на поверхности цилиндра от движения точки А по образующей ЕС и вращательного движения этой образующей. Здесь изображено несколько положений этой образующей: £0С0, £,С„ . ; при этом дуги £,£,, . равны между собой и каждая равна nd/n, где d — диаметр цилиндра, а п — число делений (на рисунке 218 п= 12). Начальное положение точки обозначено через Д), последующее через Л,, Л, и т. д.

Если при перемещении образующей из положения £0С0 в положение £,С, точка займет положение А>, то отрезок £,/1, определит расстояние, которое точка прошла по образующей от своего первоначального положения. При последующем положении образующей (£>С) точка поднимется на высоту Е2А2-2Е[А[ и т. д. Когда образующая сделает полный оборот, точка переместится по ней на расстояние ЕсАа = 12£,/1,. При дальнейшем вращении образующей точка А начнет образовывать второй виток, или оборот винтовой линии, занимая положения А, А и т. д.

На рисунке 219 выполнено построение проекций цилиндрической винтовой линии. Предварительно построены проекции (как это рассматривалось в курсе черчения средней школы) прямого кругового цилиндра. Окружность основания цилиндра (на горизонтальной проекции) и шаг (отрезок h, отложенный по оси цилиндра на фронтальной проекции) разделены на одинаковое число (п) частей; на рисунке 219 взято п- 12. Начальное положение точки А указано проекциями А» и А’ — это точка, отмеченная буквой О’ на окружности.

Так как ось цилиндра направлена перпендикулярно к плоскости ли то горизонтальная проекция винтовой линии сливается с окружностью, представляющей собой горизонтальную проекцию поверхности цилиндра.

Возможно вам будут полезны данные страницы:

Что же касается построения фронтальной проекции винтовой линии, то ход ее построения ясен из рисунка 219 и вытекает из самого образования винтовой линии как траектории точки, совершающей лва движения — равномерное по прямой линии и вместе с тем равномерное вращательное вокруг оси, параллельной этой прямой. Проекция на плоскости, параллельной оси цилиндра, в данном случае фронтальная проекция цилиндрической винтовой линии, подобна синусоиде.

На рисунке 219 фронтальная проекция винтовой линии имеет на передней (видимой) стороне цилиндра подъем слева направо или спуск влево; если же ось цилиндра расположить горизонтально, то подъем винтовой линии идет влево, а спуск — вправо. Это винтовая линия с правым ходом, или правая винтовая линия. Развертка витка цилиндрической винтовой линии показана на рисунке 220. В развернутом виде каждый виток представляет собой отрезок прямой.

Это следует из образования винтовой линии: поскольку окружность основания цилиндра делилась на равное число частей и шаг винтовой линии делился на такое же число равных частей, развертку винтовой линии на протяжении ее шага можно рассматривать как геометрическое место точек, для каждой из которых ордината пропорциональна абсциссе, т. е. у= кх. А это уравнение прямой линии. Касательные к винтовой линии совпадают на развертке с прямой, в которую развертывается виток винтовой линии.

На рисунке 220 при двух шагах

винтовой линии получились два ее отрезка под углом ф, к прямой, представляющей собой развернутую окружность основания цилиндра. Крутизна подъема винтовой линии выражается формулой (2): tg«>i=4> (2) ГШ где h — шаг винтовой линии; d — диаметр цилиндра. Угол ф, называется углом подъема винтовой линии. _

Длина одного оборота «витка» винтовой линии равна L = + (nd)2. При одном и том же d величина угла ф, зависит только от шага винтовой линии; для получения малого угла подъема следует брать малый шаг, и наоборот. Если шаг остается неизменным для цилиндров разного диаметра, то угол подъема получится тем меньше, чем больше будет диаметр цилиндра. Вопросы для самопроверки 1. В чем состоит различие между плоской и пространственной кривыми линиями?

2. Во что проецируется пространственная кривая? 3. Во что проецируется плоская кривая? 4. Во что проецируется касательная к кривой линии? 5. Как определяется длина некоторого участка кривой линии? 6. Что называется касательной к кривой линии? 7. Что называется нормалью в какой-либо точке плоской кривой? 8. Что называется шагом винтовой линии? 9. Что такое правая винтовая линия? 10. Как определяется крутизна подъема винтовой линии? 11. Какие параметры определяют цилиндрическую винтовую линию?

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Винтовая линияСкачать

Винтовая линия ⁠

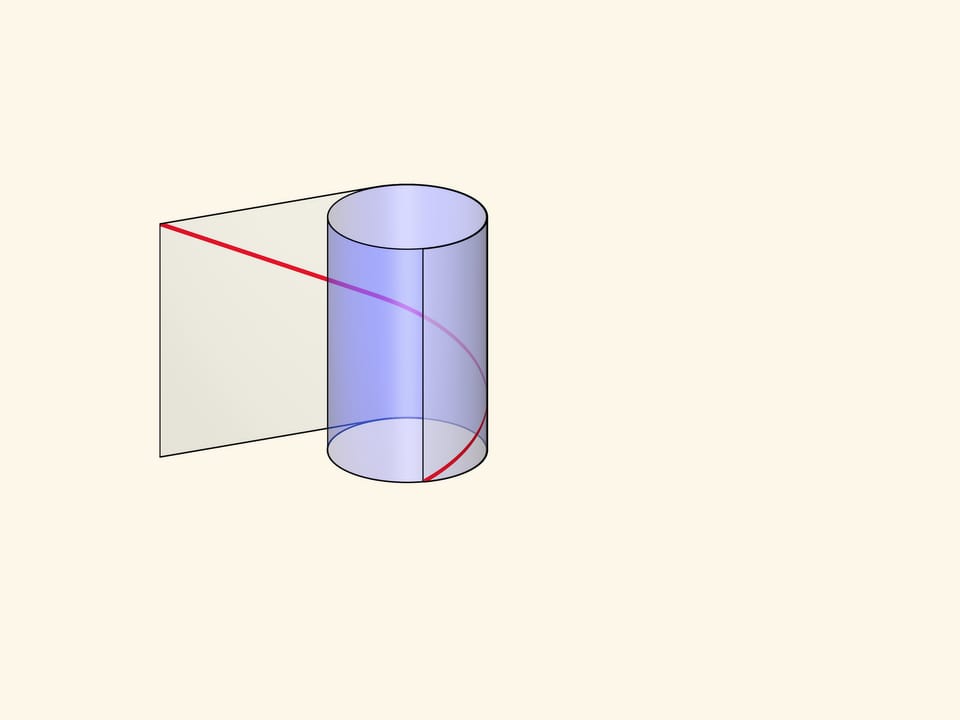
Лёгкость, с которой гайка накручивается на болт, подсказывает, что резьба одинакова по всей длине болта, а математическая суть резьбовых соединений — использование кривой, которая может скользить сама по себе. Эта замечательная кривая называется винтовой линией.

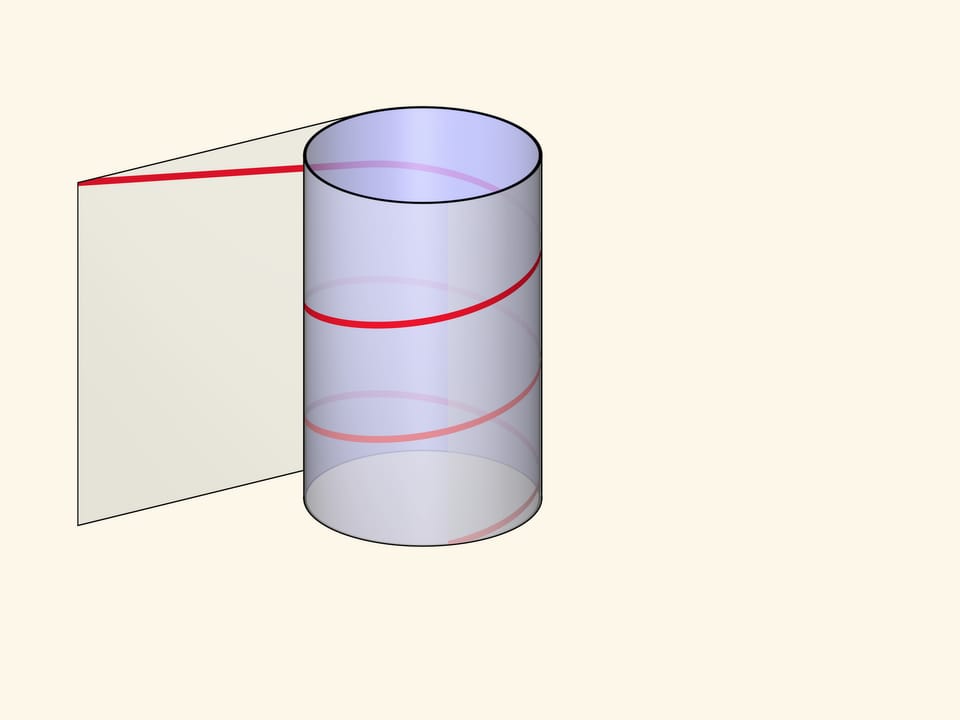
Винтовую линию можно получить, намотав на цилиндр прямоугольный прозрачный лист с отмеченной диагональю. В зависимости от длины листа и, соответственно, угла наклона нарисованной линии, будет различаться шаг винтовой линии и количество витков.

Формально винтовой линией (цилиндрической) называется линия, описываемая точкой, которая вращается с постоянной угловой скоростью вокруг неподвижной оси и одновременно перемещается вдоль этой оси с постоянной скоростью.

Наглядное представление и определение соединяются в параметрическом задании винтовой линии в прямоугольной декартовой системе координат: $$ x=a cos t,quad y=a sin t,quad z=ht. $$ Первые два уравнения показывают, что проекция точки бежит по основанию прямого кругового цилиндра радиуса $a$. Третье уравнение задаёт движение вдоль оси цилиндра с постоянной скоростью.

У «хороших» кривых в трёхмерном пространстве есть две базовые характеристики — кривизна и кручение.

Кривизна — характеризует скорость искривления линии в плоскости и определяется радиусом окружности, дуга которой наилучшим образом приближает небольшой отрезок кривой, содержащий данную точку). Кручение — скорость, с которой кривая стремится не быть плоской, насколько кривая хочет покинуть плоскость.

Замечательно, что для достаточно гладких кривых кривизна и кручение полностью определяют форму линии.

У винтовой линии кривизна и кручение постоянны, а из приведённого утверждения следует, что подобным свойством обладают только такие линии!

Постоянство кривизны и кручения во всех точках означает, что устройство винтовой линии всюду одно и то же. Как следствие, получаем, что отрезок винтовой линии может скользить вдоль неё точно так же, как отрезок — по прямой, дуга окружности — по своей окружности. (Прямую и окружность можно рассматривать как вырожденные, предельные случаи винтовой линии.)

Резьбовые соединения, в частности резьба болта или винта основаны на винтовой линии. При закручивании резьба скользит как будто по лыжне.