Уравнение виллиса и его применение

Расчет длины хода поршня и линейный расчет крутящего момента в двигателе разницы давлений в жидкости.

Основной частью конструкции двигателя разницы давлений является роторно-поршневой передаточный механизм, включающий в себя реечную и планетарную передачи. На рис.1 схематично изображена планетарная передача, включающая в себя: 1-центральное колесо(эпицикл), 2- водило(в данном механизме водило-это сам поршневой ротор), 3-сателлит. На рис.2 схематично изображена реечная передача, включающая в себя: 4-колесо реечной передачи, 5- рейка(рейка одновременно является штоком поршня), 6-гидроцилиндр поршневого ротора, 7-поршень.

Для упрощения данного расчета принимаем следующие условия: радиусы (r) реечного колеса и сателлита равны между собой, также равны между собой их угловые скорости, при этом сила давления жидкости действующая на поршень(F) будет равна силе(F) которая создаёт крутящий момент(M) на валу поршневого ротора. Длина хода поршня(L) рассчитывается по формуле:

L=2πrn Где: r-радиус колеса реечной передачи.

n-количество оборотов реечного колеса.

В силу принятых упрощённых условий количество оборотов реечного колеса будет равно количеству оборотов сателлита планетарной передачи.

Должен напомнить что сателлит вращается и движется под воздействием давления жидкости на поршень при движении в нижней части полуокружности эпицикла, в верхней полуокружности эпицикла сателлит обеспечивает обратное движение поршня до исходного положения. Движение элементов в планетарных передачах описывается формулой Виллиса, которая для данной передачи имеет следующий вид:

n=N(1-Z/z) Где: n-угловая скорость сателлита

N-угловая скорость водило

Z—число зубцов эпицикла

z-число зубцов сателлита.

Если в этом уравнении число зубцов водило и сателлита умножить на длину шага зуба, то получается отношение длины окружностей эпицикла и сателлита, после сокращения числителя и знаменателя на 2π уравнение принимает следующий вид:

n=N(1-R/r) Где: R-радиус эпицикла

r-радиус сателлита.

В силу того что в этом уравнении меня интересует не теоретический, а чисто технический результат, дальнейших преобразований производить не к чему, и решение этого уравнения будет произведено методом подстановки. Все расчеты выполняются относительно одного поршня для расчета общего крутящего момента необходимо умножить полученный результат на количество поршней в поршневом роторе.

Принимаем соотношение радиусов сателлита и эпицикла один к двум, т.е. R=2r, уравнение принимает вид:

n=N(1-2r/r);

n=N

Из этого преобразования следует что при данном соотношении радиусов сателлита и эпицикла их угловые скорости равны, что в свою очередь означает: за половину оборота водило сателлит будет также совершать половину оборота вокруг своей оси. Исходя из этого соотношения можно рассчитать длину хода поршня, которая будет составлять:

L=πr

Данная величина составляет половину длины полуокружности эпицикла. Мною неоднократно проверено следующее отношение, которое утверждает что при равенстве хода поршня, а значит и длины цилиндра поршневого ротора длине полуокружности эпицикла наступает примерное равенство крутящих моментов создаваемых давлением жидкости на поршень, и выталкивающей силы действующей на гидроцилиндр, и оно составляет:

M=1.24R²Spg Где: 1.24-коэф. неравенства среднего давления жидкости на поршень в верхней и в нижней полуокружности эпицикла.

R-радиус эпицикла;

S-площадь поршня;

p-плотность жидкости;

g-ускорение свободного падения.

Но так как было рассчитано выше с учётом формулы Виллиса, длина цилиндра будет составлять вдвое меньшую величину чем длина полуокружности эпицикла, то и величина выталкивающей силы будет соответственно вдвое меньше. На основании этого расчета крутящий момент на валу поршневого ротора будет составлять:

M=0.62R²Spg.

При соотношении радиусов сателлита и эпицикла один к трем крутящий момент на валу поршневого ротора будет меньше и составляет:

M=0,409R²Spg.

При соотношении радиусов сателлита и эпицикла один к четырем крутящий момент на валу поршневого ротора будет равен:

M=0,31R²Spg.

Эти расчеты являются еще одним доказательством работоспособности спроектированного мной гидравлического двигателя разницы давлений в жидкости. Расчет достаточно прост, и любой успевающий студент после третьего курса технического ВУЗа без труда сможет это проверить.

Уравнение виллиса и его применение

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:

• однорядный планетарный механизм;
• двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
• двухрядный планетарный механизм с двумя внешними зацеплениями;
• двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

• зубчатое колесо с внешними зубьями, расположенное в центре механизма называется «солнечным»;
• колесо с внутренними зубьями называют «короной» или «эпициклом»;
• колеса, оси которых подвижны, называют «сателлитами»;
• подвижное звено, на котором установлены сателлиты, называют «водилом» . Звено водила принято обозначать не цифрой, а латинской буквой h.

В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Общие сведения. Уравнение Виллиса

Передачи, имеющие зубчатые колёса с перемещающимися геометрическими осями — сателлитами (от лат. «satellitum» — спутник), называют планетарными. Планетарные передачи предназначены для передачи вращательного движения цилиндрическими или коническими колёсами (реже — фрикционными). Планетарная передача (планетарный ряд) состоит из малого центрального колеса («солнечная» шестерня), которое находится в постоянном зацеплении с шестернями — сателлитами, которые в свою очередь находятся в постоянном зацеплении с большим центральным колесом, называемым эпициклом (рис. 37). Оси сателлитов закреплены на элементе передачи, называемом водилой. Центральное колесо, водило и эпицикл вращаются относительно одной общей оси, называемой основной осью, в то время, как сателлиты планетарной передачи вращаются относительно собственных осей и вместе с водилом относительно общей основной оси.

В планетарной передаче крутящий момент передаётся с помощью двух из трёх элементов (центрального колеса, эпицикла или водила) при одном неподвижном. В этом проявляется одно из главных преимуществ планетарного ряда — широкие кинематические возможности, которые позволяют получать большие передаточные числа без применения многоступенчатых передач. Для простейшего планетарного ряда (рис. 34) возможны шесть включений с различными передаточными отношениями, в зависимости от того, какой из элементов неподвижен.

Рис. 34. Схема простейшей планетарной передачи:

1 — центральное колесо; 2 — эпицикл; 3 — водило; 4 — сателлит

Основным параметром, определяющим свойства планетарного ряда, является внутреннее передаточное отношение u_1-2 частоты вращения центрального колеса ω₁ к частоте вращения эпицикла ω₂. Для этого всему планетарному механизму мысленно сообщают вращение с угловой скоростью, равной по направлению и значению угловой скорости ω₃ водила 3 (приведённый планетарный механизм). В этом случае планетарный механизм представляет собой обычную зубчатую передачу с неподвижными осями, и внутреннее передаточное отношение u_1-2 будет равно:

, (4.1)

где (ω₁ – ω₃) и (ω₂ – ω₃) — угловые скорости центрального колеса 1 и эпицикла 2 относительно условно неподвижного водила 3;

z₁ и z₂ — числа зубьев центрального колеса 1 и эпицикла 2.

Уравнение (4.1) может быть записано в другом виде:

,

. (4.2)

Внутреннее передаточное отношение любого планетарного механизма — это отношение частоты вращения ω₁ центрального колеса к частоте вращения ω₂ эпицикла при остановленном водиле. В случае, если при передаче вращения центральное колесо и эпицикл вращаются в разные стороны, внутреннее передаточное отношение будет со знаком «–», если вращение происходит в одном направлении — со знаком «+».

Для схемы, изображённой на рис. 34, эпицикл, как правило, закреплён неподвижно. Тогда, согласно уравнению (4.1), передаточное отношение u_1-3 в направлении силового потока от центрального колеса 1 к водилу 3 будет равно:

ω₂ = 0, , ,

.

Для передачи силового потока в направлении от водила 3 к центральному колесу 1 передаточное отношение u_3-1 будет равно:

.

Помимо широких кинематических возможностей (большие передаточные числа) планетарная передача обладает следующими преимуществами:

— компактность (единая ось вращения всех элементов передачи);

— возможность передачи бóльших крутящих моментов в сравнении с другими зубчатыми передачами, так как крутящий момент передаётся несколькими симметрично расположенными сателлитами, что позволяет значительно снизить контактные напряжения на поверхностях зубьев;

— расположение элементов планетарного ряда позволяет достаточно просто организовать управление работой ряда (имеется в виду оборудование ленточными тормозами и блокировочными муфтами);

— работа с мéньшим шумом, чем обычные зубчатые передачи (повышенная плавность внутреннего зацепления, меньшие размеры колёс, замыкание сил в механизме и передача меньших сил на корпус).

Основными недостатками планетарных передач являются:

— значительное снижение КПД передачи при увеличении передаточного отношения;

— высокие требования к точности изготовления и монтажа.

4.2. Определение чисел зубьев зубчатых колёс планетарного ряда

Вследствие особенностей планетарных механизмов числа зубьев колёс планетарного ряда определяют, исходя из условий соосности, сборки и соседства.

Условие соосности заключается в обеспечении соосности центрального колеса, эпицикла и водила. Исходя из геометрических соотношений планетарного ряда, изображённого на рис. 4.1, условие соосности:

, , откуда

. (4.3)

Из формулы (4.3) видно, что разность чисел зубьев эпицикла и центрального колеса должна быть кратна двум. Следовательно, числа зубьев z₁ и z₂ могут быть либо чётными, либо нечётными. Случай, когда центральное колесо и эпицикл имеют чётное и нечётное (или наоборот) число зубьев, невозможен.

Рис. 35. Схема к определению условия сборки планетарного механизма

Условие сборки определяет возможность нормального зацепления зубьев центрального колеса и эпицикла с зубьями сателлитов (так как при установке одного сателлита центральное колесо и эпицикл займут взаимно — фиксированное угловое положение, то при установке остальные сателлиты должны войти в правильное зацепление с центральным колесом и эпициклом).

Пусть при сборке простейшего планетарного механизма с одновенцовыми сателлитами, изображённого на рис. 35, эпицикл неподвижен. При установке одного сателлита центральное колесо займёт определённое положение. Для установки второго сателлита необходимо повернуть водило на некоторый угол φ_в, который будет равен отношению:

, (4.4)

где n_ст — количество сателлитов в механизме.

Второй сателлит В займёт такое же положение, какое до этого занимал сателлит А. Это означает, что взаимное расположение зубьев центрального колеса и эпицикла останется прежним, и центральное колесо должно повернуться на целое число зубьев, то есть на некоторый угол φ_цк, который будет равен:

, (4.5)

где K — любое целое число;

z₁ — число зубьев центрального колеса.

Воспользуемся уравнением кинематической связи планетарного механизма при остановленном эпицикле:

, .

Так как и , то .

Подставив выражения для углов φ_цк и φ_в, получим:

, откуда . (4.6)

Таким образом, условие сборки простейшего планетарного механизма с одновенцовыми сателлитами заключается в том, что сумма чисел зубьев центрального колеса и эпицикла должна быть кратна числу сателлитов.

Рис. 36. Схема к определению условия соседства

Условие соседства исключает задевание зубьев сателлитов друг за друга. Рассмотрим два максимально сближенных сателлита (рис. 36). Из рисунка видно, что минимальное расстояние между центрами осей сателлитов О₁ и О₂ будет равно сумме двух половин делительных диаметров d_ст сателлитов и некоторого расстояния в 3m, учитывающего высоту головки зуба равной m, и считая зазор между зубьями соседних сателлитов равным m:

. (4.7)

Исходя из геометрических построений:

,

, , = .

≥ .

С учётом условия соосности (z₂ – z₁ = 2z₄, откуда ) окончательно получим:

. (4.8)

Типы планетарных механизмов

Планетарный механизм, состоящий из одного центрального колеса, одного водила и одного эпицикла, называют планетарным рядом. Планетарный ряд (механизм), все три основных звена (малое центральное колесо, эпицикл и водило) которого подвижны, называют дифференциалом.

Рис. 37. Схема дифференциального механизма автомобиля:

1 — центральное колесо; 2 — водило; 3 — сателлит

Дифференциал автомобиля является наиболее известным планетарным рядом (рис. 37). Отличительной чертой дифференциала является то, что он имеет центральные колёса одинакового размера, поэтому внутреннее передаточное отношение этого механизма равно единице. При остановке водила центральные колёса вращаются в разные стороны, поэтому передаточное отношение будет со знаком «–» (u_1-1 = –1).

Рис. 38. Схемы планетарных рядов:

а), б), в) — с положительным передаточным отношением;

г), д) — с отрицательным передаточным отношением;

1 — малое центральное колесо; 2 — эпицикл; 3 — водило; 4 — одновенцовые сателлиты; 5 — двухвенцовые сателлиты

В агрегатах мобильных машин наибольшее распространение получили так называемые плоские или простые планетарные механизмы, то есть такие, в которых все звенья вращаются в одной или параллельных плоскостях, а оси всех звеньев совпадают или параллельны друг другу и главной оси симметрии всего механизма. Плоские планетарные механизмы выполняют с одновенцовыми сателлитами (рис. 38, г), с двухвенцовыми сателлитами (рис. 38, а, в, д) и с парными сателлитами (рис. 38, б).

Если остановить водило любого планетарного механизма, то он предстанет в виде зубчатого механизма с неподвижными осями всех зубчатых колёс.

Сложные планетарные механизмы получают на основе простых путём добавления основных звеньев — солнечных колёс или эпицикла.

Свойства планетарного механизма

Свойства планетарного механизма определяют, исходя из величины внутреннего передаточного отношения, значение которого постоянно, и общего уравнения кинематической связи (4.2):

— свойство блокировки планетарного ряда: если угловые скорости двух основных звеньев планетарного ряда равны, то и угловая скорость третьего звена будет равна угловой скорости этих двух звеньев.

,

,

, и .

Если установить блокировочную муфту между любыми двумя основными звеньями планетарного ряда (например, между малым центральным колесом и эпициклом, рис. 39), то при её включении планетарный ряд будет заблокирован и его внутреннее передаточное отношение будет равно единице.

Рис. 39. Схема планетарного ряда с блокировочной муфтой:

1 — малое центральное колесо; 2 — эпицикл; 3 – водило;

4 — сателлит; 5 — блокировочная муфта

— свойство работать в режиме понижающей (в режиме редуктора) или повышающей (в режиме мультипликатора) передачи: в зависимости от выбора одного основного звена в качестве ведущего, второго — в качестве ведомого при неподвижном третьем основном звене, планетарный ряд может работать как с повышением крутящего момента, так и с понижением.

Рассмотрим это свойство на примере простейшего планетарного ряда.

На основании уравнения (4.3) можно записать уравнение кинематической связи в общем виде:

, или , (4.9)

где p,q,r — обозначения основных звеньев.

Рис. 40. Схема простейшего планетарного ряда с различным включением:

а) — при неподвижном эпицикле; б) — при неподвижном малом центральном колесе; в) — при неподвижном водиле;

1 — малое центральное колесо; 2 — эпицикл; 3 — водило; 4 — сателлит

Если необходимо составить уравнение кинематической связи в направлении силового потока, например, от водила 3 к малому центральному колесу 1 (рис. 40, а), то, согласно уравнению (4.9), u_pq → u_3-1, p → 3, q → 1, значит, r → 2. В этом случае уравнение кинематической связи примет вид:

, , .

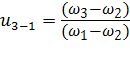
🎬 Видео