Уравнение вилли и раймера ханта

Видео:Акустические исследования на отраженных волнахСкачать

Уравнение среднего времени (Вилли) с поправкой за уплотнение

Применение поправки за уплотнение улучшает точность пористости по уравнению Вилли в плохо сцементированных песчано-глинистых чередующихся между собой пластах. Эта поправка равна 100/DTгл, где 100/DTгл — время пробега продольной волны во вмещающих глинистых пластах.

Ф = [ (DT – DTск)/( DTфл – DTск) ]*(100/DTгл)

Уравнение Раймера-Хант-Гарднера

Линейная зависимость между Ф и DT продольной волны не дает точной пористости во всем диапазоне измерений, в частности для значений пористости больше 20%. В 1980 г. Раймер, Хант и Гарднер разработали нелинейное эмпирическое уравнение, которое может быть использовано регионально, чтобы связать интервальное время пробега продольной волны с пористостью с повышенной точностью. Квадратное уравнение аппроксимировано в следующую форму:

где C=0,4-1 (0,85 в Шлюмберже)

Ключевые моменты

1. Пористость увеличивает интервальное время пробега звуковой волны через породу.

2. DTфл обычно 189 (мксек/фут). В соленых растворах часто используют пониженное значение 185 (мксек/фут).

3. В высокопористых песчаниках (>30%), с низкой водонасыщенностью и неглубоким проникновением ПЖ, значение DT может быть выше, чем в такой же среде при полной водонасыщенности.

4. Акустическое время пробега в скелете породы зависит значительно от следующих факторов:

· Вида породы (химического состава)

· Внутреннего порового давления

5. Интервальное время пробега увеличивается из-за присутствия УВ

6. Глина увеличивает DT, замедляя акустический сигнал. Следовательно, требуется поправка за глину. Эта поправка зависит от типа глин, слоистые или дисперсные.

7. Интервальное время пробега в пласте растет в присутствии УВ

8. Феномен пропуска первого вступления волны происходит, когда газ, трещины или другие аномалии ослабляют передаваемый сигнал ниже регистрируемого порога приемника

9. Акустическая пористость, рассчитанная в сцементированных песчаниках и карбонатах с межгранулярной или межкристаллической пористостью, отражает только пористость скелета

10. Акустическая пористость, рассчитанная в пластах с кавернозной или трещинной пористостью, отражает вторичную пористость и, как правило, слишком низкая, в случае применения уравнения среднего времени. В этих видах пород требуется применить добавочный метод пористости для оценки первичной пористости.

11. Часто используются следующие значения DTск:

Видео:Р.В.Шамин. Боевой функциональный анализ. № 2 "Банаховы пространства"Скачать

Выводы Дирака. Уравнение Дирака. Квантовая теория поля

Данная статья посвящена работе Поля Дирака, уравнение которого значительно обогатило квантовую механику. Она описывает основные понятия, необходимые для того, чтобы разобраться в физическом смысле уравнения, а также способы его применения.

Видео:Лекция 7. Тесты на проверку статистического различия между выборкамиСкачать

Наука и ученые

Человек, не связанный с наукой, представляет процесс добычи знаний каким-то магическим действием. А ученые, по мнению таких людей, — это чудаки, которые говорят на непонятном языке и слегка высокомерны. Знакомясь с исследователем, далекий от науки человек сразу говорит, что он в школе физику не понимал. Таким образом обыватель отгораживается от научного знания и просит более образованного собеседника говорить проще и понятнее. Наверняка Поля Дирака, уравнение которого мы рассматриваем, приветствовали так же.

Видео:Дмитрий Кесида: мир Хогвартса Джоан РоулингСкачать

Элементарные частицы

Строение вещества всегда волновало любознательные умы. В Древней Греции люди заметили, что мраморные ступени, по которым прошло множество ног, со временем меняют форму, и предположили: каждая ступня или сандалия уносила с собой крошечную частицу вещества. Эти элементы решили назвать «атомами», то есть «неделимыми». Наименование осталось, но выяснилось, что и атомы, и частицы, из которых состоят атомы, — тоже составные, сложные. Эти частицы называются элементарными. Именно им посвящена работа Дирака, уравнение которого позволило не только объяснить спин электрона, но и предположить наличие антиэлектрона.

Видео:К. В. Райхерт # Философия Чарльза Уильяма МоррисаСкачать

Корпускулярно-волновой дуализм

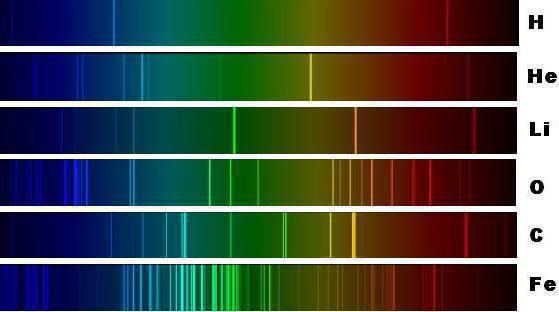
Развитие техники фотографии в конце девятнадцатого века повлекло за собой не только моду на запечатление себя, еды и кошек, но и продвинуло возможности науки. Получив такой удобный инструмент, как быстрая фотография (напомним, раньше выдержки доходили до 30-40 минут), ученые стали массово фиксировать разнообразные спектры.

Существующие на тот момент теории строения веществ не могли однозначно объяснить или предсказать спектры сложных молекул. Сначала знаменитый опыт Резерфорда доказал, что атом не такой уж неделимый: в его центре находилось тяжелое положительное ядро, вокруг которого располагались легкие отрицательные электроны. Потом открытие радиоактивности доказало, что и ядро не монолит, а состоит из протонов и нейтронов. А дальше почти одновременное открытие кванта энергии, принципа неопределенности Гейзенберга и вероятностной природы местоположения элементарных частиц дали толчок к развитию принципиально иного научного подхода к изучению окружающего мира. Появился новый раздел – физика элементарных частиц.

Основным вопросом на заре этого века великих открытий в сверхмалых масштабах стало объяснение наличия у элементарных частиц и массы, и свойств волны.

Эйнштейн доказал, что даже неуловимый фотон обладает массой, так как передает импульс твердому телу, на который падает (явление давления света). При этом многочисленные опыты по рассеянию электронов на щелях говорили как минимум о наличии у них дифракции и интерференции, это свойственно только волне. В итоге пришлось признать: элементарные частицы одновременно и объект с массой, и волна. То есть масса, скажем, электрона как бы «размазана» в пакет энергии с волновыми свойствами. Этот принцип корпускулярно-волнового дуализма позволил объяснить прежде всего, почему электрон не падает на ядро, а также по каким причинам в атоме существуют орбиты, а переходы между ними скачкообразные. Эти переходы и порождают спектр, уникальный для любого вещества. Далее физика элементарных частиц должна была объяснить свойства самих частиц, а также их взаимодействие.

Видео:Общее языкознание - 8. Сравнительно-исторический и структурные методы.Скачать

Волновая функция и квантовые числа

Эрвин Шредингер совершил удивительное и до сих пор малопонятное открытие (на его основании чуть позже Поль Дирак построил свою теорию). Он доказал, что состояние любой элементарной частицы, например, электрона описывает волновая функция ψ. Сама по себе она ничего не значит, а вот ее квадрат покажет вероятность найти электрон в данном месте пространства. При этом состояние элементарной частицы в атоме (или другой системе) описывается четырьмя квантовыми числами. Это главное (n), орбитальное (l), магнитное (m) и спиновое (m_s) числа. Они показывают свойства элементарной частицы. Как аналогию можно привести брусок масла. Его характеристики – масса, размер, цвет и жирность. Однако свойства, описывающие элементарные частицы, нельзя понять интуитивно, их надо осознавать через математическое описание. Работа Дирака, уравнение которого — в центре внимания этой статьи, посвящена последнему, спиновому числу.

Прежде чем перейти непосредственно к уравнению, необходимо объяснить, что же обозначает спиновое число m_s. Оно показывает собственный момент импульса электрона и других элементарных частиц. Это число всегда положительно и может принимать целое значение, ноль или полуцелое значение (для электрона m_s = 1/2). Спин – величина векторная и единственная, которая описывает ориентацию электрона. Квантовая теория поля кладет спин в основу обменного взаимодействия, которому нет никакого аналога в обычно интуитивно понятной механике. Спиновое число показывает, каким образом должен повернуться вектор, чтобы прийти в изначальное состояние. Примером может служить обычная шариковая ручка (пишущая часть пусть будет положительным направлением вектора). Чтобы она пришла в изначальное состояние, ее надо повернуть на 360 градусов. Такая ситуация соответствует спину, равному 1. При спине 1/2, как у электрона, поворот должен быть 720 градусов. Так что, помимо математического чутья, надо иметь развитое пространственное мышление, чтобы понять это свойство. Чуть выше шла речь о волновой функции. Она является основным «действующим лицом» уравнения Шредингера, с помощью которого описывается состояние и положение элементарной частицы. Но это соотношение в своем изначальном виде предназначено для частиц без спина. Описать состояние электрона можно, только если провести обобщение уравнения Шредингера, что и было проделано в работе Дирака.

Видео:Витрувий: Десять книг об архитектуре. Классики теории архитектуры. История архитектуры. АудиокнигаСкачать

Бозоны и фермионы

Фермион – частица с полуцелым значением спина. Фермионы располагаются в системах (например атомах) согласно принципу Паули: в каждом состоянии должно быть не более одной частицы. Таким образом, в атоме каждый электрон чем-то отличается от всех остальных (какое-то квантовое число имеет другое значение). Квантовая теория поля описывает и другой случай – бозоны. Они имеют целый спин и могут все одновременно быть в одном состоянии. Реализация этого случая называет Бозе-конденсацией. Несмотря на достаточно хорошо подтвержденную теоретическую возможность его получить, практически это осуществили только в 1995 году.

Видео:Лекция «Город на реке Амстел: археологическое исследование Амстердама» | Ежи ГавронскиСкачать

Уравнение Дирака

Как мы уже говорили выше, Поль Дирак вывел уравнение классического поля электрона. Оно также описывает состояния других фермионов. Физический смысл соотношения сложен и многогранен, и из его формы следует много фундаментальных выводов. Вид уравнения следующий:

где m — масса фермиона (в частности электрона), с — скорость света, p_k— три оператора компонент импульса (по осям x, y, z), ħ — урезанная постоянная Планка, x и t – три пространственные координаты (соответствуют осям X, Y, Z) и время, соответственно, и ψ(x, t) — четырёхкомпонентная комплексная волновая функция, α_k (k=0, 1, 2, 3) — матрицы Паули. Последние представляют собой линейные операторы, которые действуют на волновую функцию и ее пространство. Формула эта довольно сложная. Чтобы понять хотя бы ее компоненты, надо разбираться в основных определениях квантовой механики. Также следует обладать недюжинными математическими познаниями, чтобы как минимум знать, что такое вектор, матрица и оператор. Специалисту вид уравнения скажет еще больше, чем его компоненты. Человек, сведущий в ядерной физике и знакомый с квантовой механикой, поймет важность этого соотношения. Однако надо признаться, что уравнения Дирака и Шредингера — всего лишь элементарные основы математического описания процессов, которые происходят в мире квантовых величин. Физики-теоретики, которые решили посвятить себя элементарным частицам и их взаимодействию, должны понимать суть этих соотношений на первом-втором курсах института. Но наука эта увлекательная, и именно в этой области можно совершить прорыв или увековечить свое имя, присвоив его уравнению, преобразованию или свойству.

Видео:Лекция Жюли Реше «Мунк и крик мира»Скачать

Физический смысл уравнения

Как мы и обещали, рассказываем, какие выводы таит уравнение Дирака для электрона. Во-первых, из этого соотношения становится ясно, что спин электрона равен ½. Во-вторых, согласно уравнению, у электрона есть собственный магнитный момент. Он равен магнетону Бора (единица элементарного магнитного момента). Но самый главный результат получения этого соотношения кроется в незаметном операторе α_k. Вывод уравнения Дирака из уравнения Шредингера занял много времени. Вначале Дирак думал, что эти операторы мешают соотношению. С помощью разных математических ухищрений он пытался исключить их из уравнения, но ему это не удалось. В итоге уравнение Дирака для свободной частицы содержит четыре оператора α. Каждый из них представляет собой матрицу [4×4]. Два соответствуют положительной массе электрона, что доказывает наличие двух положений его спина. Другие же два дают решение для отрицательной массы частицы. Самые простые познания в физике предоставляют человеку возможность заключить, что это невозможно в реальности. Но в результате эксперимента выяснилось, что последние две матрицы являются решениями для существующей частицы, противоположной электрону – антиэлектрону. Как и электрон, позитрон (так назвали эту частицу) обладает массой, но его заряд положителен.

Видео:Roman Karasev, Covering dimension using toric varietiesСкачать

Позитрон

Как часто бывало в эру квантовых открытий, Дирак сначала не поверил собственному выводу. Он не решился открыто опубликовать предсказание новой частицы. Правда, во множестве статей и на различных симпозиумах ученый подчеркивал возможность ее существования, хотя и не постулировал это. Но вскоре после вывода этого знаменитого соотношения позитрон был найден в составе космического излучения. Таким образом, его существование было подтверждено эмпирически. Позитрон – первый найденный людьми элемент антиматерии. Позитрон рождается как один из близнецов пары (другой близнец – это электрон) при взаимодействии фотонов очень высокой энергии с ядрами материи в сильном электрическом поле. Приводить цифры мы не будем (заинтересованный читатель и сам найдет всю нужную информацию). Однако стоит подчеркнуть, что речь идет о космических масштабах. Произвести фотоны нужной энергии способны лишь взрывы сверхновых и столкновения галактик. Также они в некотором количестве содержатся в ядрах горячих звезд, в том числе Солнца. Но человек всегда стремится к своей выгоде. Аннигиляция материи с антиматерией дает много энергии. Чтобы обуздать этот процесс и пустить его на благо человечества (например, эффективными были бы двигатели межзвездных лайнеров на аннигиляции), люди научились изготавливать протоны в лабораторных условиях.

В частности, большие ускорители (типа адронного коллайдера) могут создавать пары электрон-позитрон. Раньше также высказывались предположения, что существуют не только элементарные античастицы (помимо электрона их еще несколько), но и целая антиматерия. Даже совсем небольшой кусочек любого кристалла из антивещества обеспечил бы энергией всю планету (может быть, криптонит супермена был антиматерией?).

Но увы, создание антиматерии тяжелее ядер водорода в обозримой вселенной задокументировано не было. Однако если читатель думает, что взаимодействие вещества (подчеркнем, именно вещества, а не отдельно взятого электрона) с позитроном сразу заканчивается аннигиляцией, то он ошибается. При торможении позитрона с высокой скоростью в некоторых жидкостях с ненулевой вероятностью возникает связанная пара электрон-позитрон, которая называется позитроний. Это образование имеет некоторые свойства атома и даже способно вступать в химические реакции. Но существует этот хрупкий тандем недолго и потом все равно аннигилирует с испусканием двух, а в некоторых случаях и трех гамма-квантов.

Видео:Лекция Анны Вяземцевой «Реконструкция Рима в 1920-1930е годы»Скачать

Недостатки уравнения

Несмотря на то что благодаря этому соотношению был обнаружен антиэлектрон и антиматерия, оно имеет существенный недостаток. Запись уравнения и модель, построенная на его основе, не способны предсказать, как рождаются и уничтожаются частицы. Это своеобразная ирония квантового мира: теория, предсказавшая рождение пар материя-антиматерия, не способна адекватно описать этот процесс. Данный недостаток был устранен в квантовой теории поля. Путем введения квантованности полей эта модель описывает их взаимодействие, в том числе рождение и уничтожение элементарных частиц. Под «квантовой теорией поля» в данном случае подразумевается совершенно конкретный термин. Это область физики, которая изучает поведение квантовых полей.

Видео:А. Аствацатуров - Лекция №6 Уильям Фолкнер. Шум и яростьСкачать

Уравнение Дирака в цилиндрических координатах

Для начала сообщим, что такое цилиндрическая система координат. Вместо привычных трех взаимно перпендикулярных осей для определения точного местоположения точки в пространстве используются угол, радиус и высота. Это то же самое, что полярная система координат на плоскости, только добавляется третье измерение – высота. Эта система удобна, если требуется описать или исследовать некоторую поверхность, симметричную относительно одной из осей. Для квантовой механики это весьма полезный и удобный инструмент, который позволяет значительно сократить размер формул и количество вычислений. Это следствие осесимметричности электронного облака в атоме. Уравнение Дирака в цилиндрических координатах решается несколько иначе, чем в привычной системе, и дает иногда неожиданные результаты. Например, некоторые прикладные задачи по определению поведения элементарных частиц (чаще всего электронов) в квантованном поле решались преобразованием вида уравнения к цилиндрическим координатам.

Видео:ХаосСкачать

Использование уравнения для определения строения частиц

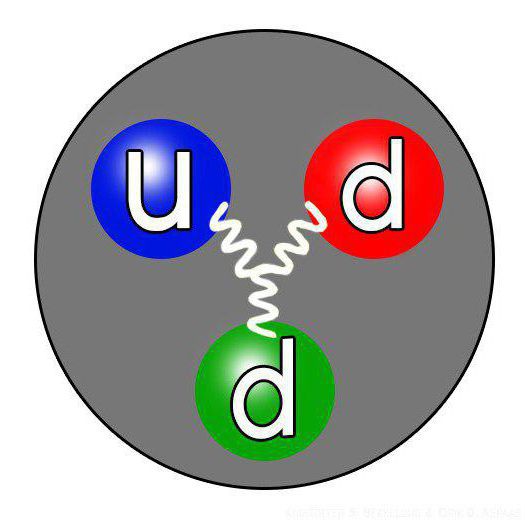
Это равенство описывает простые частицы: такие, которые не состоят из еще более мелких элементов. Современная наука способна измерять магнитные моменты с достаточно высокой точностью. Таким образом, несоответствие посчитанного с помощью уравнения Дирака значения измеренному экспериментально магнитному моменту будет косвенно свидетельствовать о сложном строении частицы. Напомним, это равенство применимо к фермионам, их спин полуцелый. С помощью этого уравнения была подтверждена сложная структура протонов и нейтронов. Каждый из них состоит из еще более мелких элементов, которые называются кварками. Глюонное поле держит кварки вместе, не давая им рассыпаться. Существует теория, что и кварки — это не самые элементарные частицы нашего мира. Но пока у людей не хватает технической мощи, чтобы это проверить.

Видео:🌉 Приглашение на курс Давида Дэйча по книге Р. Йоэля Торджмана "Ха-Гешер"Скачать

Petroleum Engineers

Видео:Стохастический анализ, Лекция 2: Винеровский процессСкачать

Вы здесь

Видео:Ошибка Рональда Рейгана // Хайлайты Михаила СветоваСкачать

Уравнение Гарднера

Коллеги, подскажите плз — кто встречал работы по определению коефициентов уравнения Гарднера по отношению к месторождениям СНГ ?

Коллеги, подскажите плз — кто встречал работы по определению коефициентов уравнения Гарднера по отношению к месторождениям СНГ ?

в первом случае пористоть по плотности приравнивается к пористости по акустике. С точки зрения физики — бред.
во втором — вводится «нормализующий» коэффициэнт типа уплотнения глин. А на практике — подгоняется под керн или нейтрон-плотностную пористось.

прошу прощения, не знал что их так много, Гарднеров, я имел в виду эмпирическую зависимость плотность-скорость продольной волны
http://www.ipt.ntnu.no/pyrex/stash/GPY00770.pdf

в первом случае пористоть по плотности приравнивается к пористости по акустике. С точки зрения физики — бред.
во втором — вводится «нормализующий» коэффициэнт типа уплотнения глин. А на практике — подгоняется под керн или нейтрон-плотностную пористось.

Для Западной Сибири встречал эмпирические формулы для определения пластовых скоростей и плотности:
А.П. Базылев, В.Н. Сургучева, Т.К. Снопкова. Восстановление акустических характеристик разрезов в отложениях Западной Сибири. Геофизика, Спецвыпуск, 2001.

Для Западной Сибири встречал эмпирические формулы для определения пластовых скоростей и плотности:
А.П. Базылев, В.Н. Сургучева, Т.К. Снопкова. Восстановление акустических характеристик разрезов в отложениях Западной Сибири. Геофизика, Спецвыпуск, 2001.

да, что то типо того. бред? ну может и да, как говаривает один математик — я вообще не понимаю как работают гисовци — два яблока плюс одна груша получается.

Для З Сибири (Широтное Приобье) Dt хорошо «восстанавливалась» из эмпирики RHOB-TVD. Строились два тренда уплотнения — для чистых глинистых разностей, и для чистых песчаных разностей, для каждого выводилась своя зависисмость, ну и потом окончательный результат. с учетом Vcl (ГК) как пропорция

Для «полировки» выделялись угли, Бажен и карбонатизированные прослои у которых были свои тренды. синтетики получал с коэффициэнтом корреляции по энергии 0.75-0.8

🎥 Видео

Встреча 31. О теории управления, связностях в расслоениях и пространстве Карно-КаратеодориСкачать

Р.Н.Карасев Кратности отображений и конфигурационные пространстваСкачать

#3 Архитектура с краеведом Геннадием КрольманомСкачать

Михаил Веллер – Перпендикуляр. [Аудиокнига]Скачать