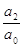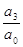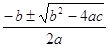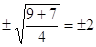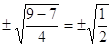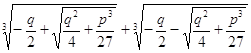Уравнение виета для высших степеней

Видео:Теорема Виета для уравнений высших степеней. Рациональные уравнения Часть 4 из 4Скачать

Формула Виета для многочленов (уравнений) высших степеней

2.5 Формула Виета для многочленов (уравнений) высших степеней

Формулы, выведенные Виетом для квадратных уравнений, верны и для многочленов высших степеней.

В этом случае он имеет разложение на множители вида:

Разделим обе части этого равенства на a₀ ≠ 0 и раскроем в первой части скобки. Получим равенство:

x n + ()x n -1 + … + () = x n – (x₁ + x₂ + … + x_n) x n -1 + ( x₁x₂ + x₂x₃ + … + x_n-1x_n)x n -2 + … +(-1) n x₁x₂ … x_n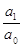

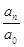
Но два многочлена тождественно равны в том и только в том случае, когда коэффициенты при одинаковых степенях равны. Отсюда следует, что выполняется равенство

x₁ + x₂ + … + x_n= —

x₁x₂ + x₂x₃ + … + x_n-1x_n=

x₁x₂ … x_n= (-1) n

Например, для многочленов третей степени

x₁ + x₂ + x₃ = —

x₁x₂ + x₁x₃ + x₂x₃ =

x₁x₂x₃ = —

Как и для квадратных уравнений, эту формулу называют формулами Виета. Левые части этих формул являются симметрическими многочленами от корней x₁ , x₂ …, x_nданного уравнения, а правые части выражаются через коэффициент многочлена.

2.6 Уравнения, сводимые к квадратным (биквадратные)

К квадратным уравнениям сводятся уравнения четвертой степени:

ax 4 + bx 2 + c = 0,

называемые биквадратными, причем, а ≠ 0.

Достаточно положить в этом уравнении х 2 = y, следовательно,

найдём корни полученного квадратного уравнения

y_1,2 =

Чтобы найти сразу корни х_1,x_2,x_3,x₄ , заменим y на x и получим

x² =

х_1,2,3,4 = .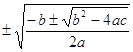

Если уравнение четвёртой степени имеет х₁, то имеет и корень х₂ = -х₁,

Если имеет х₃, то х₄ = — х₃. Сумма корней такого уравнения равна нулю.

Подставим уравнение в формулу корней биквадратных уравнений:

х_1,2,3,4 = ,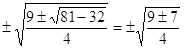

х_1,2 =

х_3,4 =

Ответ: х_1,2 = ±2; х_1,2 =

2.7 Исследование биквадратных уравнений

Возьмем биквадратное уравнение

ax 4 + bx 2 + c = 0,

где a, b, c –действительные числа, причем а > 0. Введя вспомогательную неизвестную y = x², исследуем корни данного уравнения, и результаты занесем в таблицу (см. приложение №1)

2.8 Формула Кардано

Если воспользоваться современной символикой, то вывод формулы Кардано может иметь такой вид:

х =

Эта формула определяет корни общего уравнения третей степени:

ax 3 + 3bx 2 + 3cx + d = 0.

Эта формула очень громоздкая и сложная (она содержит несколько сложныных радикалов). Она не всегда примениться, т.к. очень сложна для заполнения.

Видео:Теорема БезуСкачать

Теорема Виета для квадратных и других уравнений

Видео:Теорема Виета для многочлена 3 порядка. 10 класс.Скачать

Квадратные уравнения

Теорема Виета

Пусть и обозначают корни приведенного квадратного уравнения
(1) .
Тогда сумма корней равна коэффициенту при , взятому с обратным знаком. Произведение корней равно свободному члену:
;
.

Замечание по поводу кратных корней

Если дискриминант уравнения (1) равен нулю, то это уравнение имеет один корень. Но, чтобы избежать громоздких формулировок, принято считать, что в этом случае, уравнение (1) имеет два кратных, или равных, корня:
.

Доказательство первое

Находим сумму корней:
.

Чтобы найти произведение, применим формулу:
.
Тогда

.

Доказательство второе

Если числа и являются корнями квадратного уравнения (1), то
.
Раскрываем скобки.

.
Таким образом, уравнение (1) примет вид:
.
Сравнивая с (1) находим:
;
.

Обратная теорема Виета

Пусть и есть произвольные числа. Тогда и являются корнями квадратного уравнения
,
где
(2) ;
(3) .

Доказательство обратной теоремы Виета

Рассмотрим квадратное уравнение
(1) .
Нам нужно доказать, что если и , то и являются корнями уравнения (1).

Подставим (2) и (3) в (1):
.
Группируем члены левой части уравнения:
;
;
(4) .

Подставим в (4) :
;
.
Уравнение выполняется. То есть число является корнем уравнения (1).

Подставим в (4) :
;
.
Уравнение выполняется. То есть число является корнем уравнения (1).

Теорема Виета для полного квадратного уравнения

Теперь рассмотрим полное квадратное уравнение
(5) ,
где , и есть некоторые числа. Причем .

Разделим уравнение (5) на :
.
То есть мы получили приведенное уравнение
,
где ; .

Тогда теорема Виета для полного квадратного уравнения имеет следующий вид.

Пусть и обозначают корни полного квадратного уравнения
.
Тогда сумма и произведение корней определяются по формулам:
;
.

Видео:Вспоминаем схему Горнера и уравнения высших степенейСкачать

Теорема Виета для кубического уравнения

Аналогичным образом мы можем установить связи между корнями кубического уравнения. Рассмотрим кубическое уравнение
(6) ,
где , , , есть некоторые числа. Причем .
Разделим это уравнение на :
(7) ,
где , , .
Пусть , , есть корни уравнения (7) (и уравнения (6)). Тогда

.

Сравнивая с уравнением (7) находим:
;
;
.

Видео:✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать

Теорема Виета для уравнения n-й степени

Тем же способом можно найти связи между корнями , , . , , для уравнения n-й степени
.

Теорема Виета для уравнения n-й степени имеет следующий вид:
;
;
;

.

Чтобы получить эти формулы мы записываем уравнение в следующем виде:
.
Затем приравниваем коэффициенты при , , , . , и сравниваем свободный член.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
С.М. Никольский, М.К. Потапов и др., Алгебра: учебник для 8 класса общеобразовательных учреждений, Москва, Просвещение, 2006.

Автор: Олег Одинцов . Опубликовано: 05-10-2016

Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Уравнения высших степеней

Вы будете перенаправлены на Автор24

Уравнения высших степеней — это уравнения, в которых старшая степень при переменной больше либо равна трём. На данный момент не существует какой-либо единой схемы для решения уравнений высших степеней.

Наиболее известными схемами для решения являются:

• Формула Кардано, он подходит только для уравнений 3-ьей степени;
• Метод Феррари для уравнений 4-ой степени;
• Теорема Виета для степени больше двух;
• Теорема Безу;
• Схема Горнера.

Ниже рассмотрены основные методы решения уравнений высших степеней с целыми и рациональными коэффициентами, справедливые для разных степеней.

Видео:8 класс, 35 урок, Уравнения высших степенейСкачать

Теорема Виета

Рассмотрим уравнение вида $ax^3+bx^2+cx+d=0$.

Данное уравнение обладает тремя корнями и для того чтобы его решить в общем виде, необходимо решить следующую систему:

Иначе эти системы уравнений также называют формулами Виета.

Решите уравнение: $x^3+x^2-4x-4=0$.

Решение:

Составим систему уравнений:

$begin x_1+ x_2+x_3=-frac \ x_1 cdot x_2 + x_2 cdot x_3 + x_1 cdot x_3=-frac=-4 \ x_1 cdot x_2 cdot x_3= -frac\ end$

Решив её, получим следующие корни:

Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Теорема Безу

Суть этой теоремы в том, что если уравнение вида $a_0x^n + a_1x^+a_2x^+. +a_x+a_n=0$ с ненулевым свободным членом имеет некий корень $α$, принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.

Алгоритм при решении уравнения с использованием теоремы Безу следующий:

1. Найти и выписать все делители свободного члена.
2. Проверять эти делители до тех пор, пока не будет найден хотя бы один, являющийся корнем уравнения.
3. Разделить всё уравнение на $(x-α)$ и записать само уравнение как произведение $(x-α)$ и результата выполненного деления.
4. Решить полученное после разложения уравнение.

Готовые работы на аналогичную тему

Решение:

Делители члена не при переменной: $±1;±2;±3;±6$

Подставим $1$ в корень уравнения и получим, что наше равенство выполняется:

Следовательно, $x_1=1$ — один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком:

Рисунок 1. Схема деления многочлена столбиком. Автор24 — интернет-биржа студенческих работ

После этого исходное уравнение можно записать разложив на множители:

Решаем полученное квадратное уравнение и получаем ещё 2 корня: $x_=-3;-2$.

Видео:Метод неопределенных коэффициентовСкачать

Схема Горнера

Схема Горнера состоит в том, чтобы также сначала найти какой-либо корень уравнения вида $a_0x^n + a_1x^+a_2x^+. +a_x+a_n=0$ через делители свободного члена.

После этого составляется специальная таблица с результатами деления на $(x-α)$, в которой каждый член зависим от предыдущего. Коэффициенты из данной таблицы используются как коэффициенты в полученном от деления частного многочлене, они вычисляются по формулам:

$b_0=a_0; b_1=αb_0+a_1; b_2=αb_1+a_2. b_= αb_+a_;b_n=αb_+a_n$.

Рисунок 2. Таблица для вычисления коэффициентов по схеме Горнера. Автор24 — интернет-биржа студенческих работ

Решение:

Делители свободного члена — $±1;±2;±3;±6$

Запишем таблицу со коэффициентами:

Рисунок 3. Схема Горнера: пример. Автор24 — интернет-биржа студенческих работ

Отсюда получаем, что многочлен, полученный от деления на $(x-α)$ при $α=1$, равен $x^2+5x+6$.Получается, что исходное уравнение принимает вид:

Корни же второго многочлена будут $x_=-2;-3$.

Видео:Уравнение четвертой степениСкачать

Метод одновременного подбора по коэффициенту при старшей степени и при свободном члене

Данный метод основан на следующем условии:

Несократимая дробь $frac

$ будет корнем уравнения, если числитель этой дроби является делителем свободного члена, а знаменатель — делителем коэффициента, стоящего при члене со старшей степенью.

Алгоритм этого метода:

1. Поиск делителей свободного члена.
2. Поиск делителей коэффициента, стоящего при члене со старшей степенью.
3. Составление дробей и подбор решения.

Решение:

Делители свободного члена: $±1; ±2; ±3; ±6$.

Делители коэффициента при старшем члене: $1; 2$.

Следовательно, как корни нужно проверить следующие значения: $1;-1;2;-2;3;-3;6;-6;frac; -frac; frac; -frac$.

Подставив эти числа в уравнения, получим, что корнями уравнения являются $x_1=1;x_2= frac$.

Это значит, что многочлен можно разделить на $2(x-1)(x-frac)=2x^2-3x+1$. При выполнении деления получаем частное $x^2+10x+6$.

Приравниваем этот многочлен к нулю и находим его корни через дискриминант, они равны $x_=-5±sqrt$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 14 03 2021

📸 Видео

Уравнения высших степеней 1 часть (старший коэффициент равен 1)Скачать

Уравнения высших степеней. Решение уравнений с помощью деления в столбикСкачать

✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

Математика | Кубические уравнения по методу СталлонеСкачать

Решение биквадратных уравнений. 8 класс.Скачать

2.2. Рациональные уравнения. Теоремы Виета и Безу. Уравнения высших степеней.Скачать

Схема Горнера. 10 класс.Скачать

УДИВИТЕЛЬНЫЙ способ решения уравнения 4-ой степениСкачать