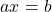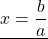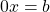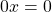Уравнение вида ax b где x переменная (5 видео)

Уравнение с одним неизвестным

Уравнение вида ax = b, где x — неизвестное, a и b — числа, называется уравнением с одним неизвестным или линейным уравнением.

Число a называется коэффициентом при неизвестном, а число b — свободным членом.

Если в уравнении ax = b коэффициент не равен нулю (a ≠ 0), то, разделив обе части уравнения на a, получим . Значит, уравнение ax = b, в котором a ≠ 0, имеет единственный корень .

Если в уравнении ax = b коэффициент равен нулю (a = 0), а свободный член не равен нулю (b ≠ 0), то уравнение не имеет корней, так как равенство 0x = b, где b ≠ 0, не является верным ни при каком значении x.

Если в уравнении ax = b и коэффициент, и свободный член равны нулю (a = 0 и b = 0), то уравнение имеет бесконечное множество корней, так как равенство 0x = 0 верно при любом значении x.

Содержание

Решение уравнений с одним неизвестным
Что такое линейное уравнение
1. Уравнение вида ах=в, где х — переменная, а и в — некоторые числа, называется линейным уравнением с одной переменной. 1. Уравнение вида ах=в, где х. — презентация
Похожие презентации
Презентация на тему: » 1. Уравнение вида ах=в, где х — переменная, а и в — некоторые числа, называется линейным уравнением с одной переменной. 1. Уравнение вида ах=в, где х.» — Транскрипт:
📸 Видео

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Решение уравнений с одним неизвестным

Все уравнения с одним неизвестным решаются одинаково с помощью преобразований, которые могут выполняться в любом порядке. Список возможных преобразований, которые могут быть использованы для решения уравнений:

освобождение от дробных членов;
раскрытие скобок;
перенос всех членов, содержащих неизвестное, в одну часть, а известные — в другую (члены с неизвестными, как правило, переносят в левую часть уравнения);
сделать приведение подобных членов;
разделить обе части уравнения на коэффициент при неизвестном.

Пример 1. Решить уравнение

20x — 28 — 24 = 9x + 36.

20x — 9x = 36 + 28 + 24.

Выполняем приведение подобных членов:

Делим обе части уравнения на коэффициент при неизвестном (на 11):

Делаем проверку, подставив в данное уравнение вместо x его значение:

Уравнение обратилось в верное равенство, следовательно, корень был найден верно.

Пример 2. Решить уравнение

Выполняем приведение подобных членов:

Делаем проверку, подставив в данное уравнение вместо x его значение:

5(11 — 2) = 45;
5 · 9 = 45;
45 = 45.

Обычно все рассуждения при решении уравнения производят устно, а само решение записывается так:

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Что такое линейное уравнение

Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?

В курсе алгебры 7 класса линейное уравнение определяется следующим образом.

Определение.

Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.

Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.

Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:

Количество корней линейного уравнения зависит от значения a (коэффициента перед x).

При a≠0 линейное уравнение имеет единственное решение.

Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:

Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).

В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).

При a=0, b≠0 линейное уравнение

При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.

При a=0, b=0 линейное уравнение

имеет бесконечное множество решений.

При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.

Возможные решения линейных уравнений можно изобразить в виде схемы.

Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.

Решение многих уравнений сводится к решению линейных уравнений.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

1. Уравнение вида ах=в, где х — переменная, а и в — некоторые числа, называется линейным уравнением с одной переменной. 1. Уравнение вида ах=в, где х. — презентация

Презентация была опубликована 6 лет назад пользователемИгорь Самарин

Презентация на тему: » 1. Уравнение вида ах=в, где х — переменная, а и в — некоторые числа, называется линейным уравнением с одной переменной. 1. Уравнение вида ах=в, где х.» — Транскрипт:

2 1. Уравнение вида ах=в, где х — переменная, а и в — некоторые числа, называется линейным уравнением с одной переменной. 1. Уравнение вида ах=в, где х — переменная, а и в — некоторые числа, называется линейным уравнением с одной переменной. Примеры: 5 х=-4; — 0,2 х=0; -х =- Примеры: 5 х=-4; — 0,2 х=0; -х =-

3 1) Если а 0, то х= -единственный корень. 1) Если а 0, то х= -единственный корень. Например: -10 х=45; х=- ; х= -4,5. Например: -10 х=45; х=- ; х= -4,5. 2) Если а=0 и в 0,то уравнение ах = в не имеет корней, так как равенство 0 х=в не является верным ни при каком х. 2) Если а=0 и в 0,то уравнение ах = в не имеет корней, так как равенство 0 х=в не является верным ни при каком х. Например, 0 х=16; 0 х= -48,3. Например, 0 х=16; 0 х= -48,3. 3)Если а=0 и в=0, то любое значение х является корнем уравнения, так как равенство 0 х=0 верно при любом х. 3)Если а=0 и в=0, то любое значение х является корнем уравнения, так как равенство 0 х=0 верно при любом х.

4 3. Решим уравнение 4(х+7)=3-х, раскроем скобки 3. Решим уравнение 4(х+7)=3-х, раскроем скобки 4 х+28=3-х перенесём слагаемое –х в левую часть уравнения, а 28 в правую часть, изменив при этом их знаки. 4 х+28=3-х перенесём слагаемое –х в левую часть уравнения, а 28 в правую часть, изменив при этом их знаки. 4 х+х=3-28, 4 х+х=3-28, 5 х= -25, 5 х= -25, х= -25:5, х= -25:5, х= -5. х= -5. Ответ: х=-5. Ответ: х=-5.

5 4. Если при решении уравнения приходим к равносильному ему линейному уравнению вида 0 х=в, то в этом случае либо исходное уравнение не имеет корней,либо его корнем является любое число: а)Решим уравнение: 2 х+5=2(х+6);2 х+5=2 х+12;2 х-2 х=12-5;0 х=7. Ответ: корней нет. б) 3(х+2)+х=6+4 х; 3 х+6+х=6+4 х; 3 х+6+х=6+4 х; 3 х+х-4 х=6-6; 3 х+х-4 х=6-6; 0 х=0. 0 х=0. Ответ: любое число.