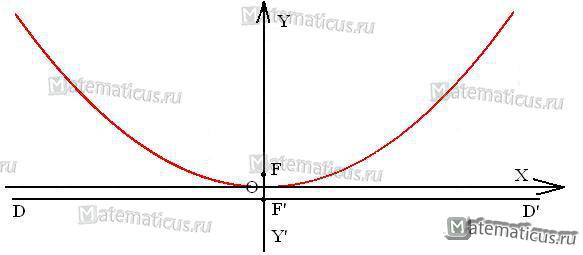
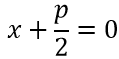Парабола есть геометрическое место точек M, равноудалённых от данной точки F и данной прямой DD’:
FM=KM.
F – фокус;
DD’ – директриса;
FC=p – расстояние от фокуса до директрисы называется параметром параболы;
CO=OF= $frac
$
O – точка, которая является вершиной параболы.
- Каноническое уравнение параболы (ветви параболы направлены вправо)
- Уравнение директрисы DD’
- Квадратичная функция. Построение параболы
- Основные понятия
- Построение квадратичной функции
- Алгоритм построения параболы
- Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
- Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
- Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
- Уравнение ветви параболы направленной вправо
- 📺 Видео
Видео:Как легко составить уравнение параболы из графикаСкачать

Каноническое уравнение параболы (ветви параболы направлены вправо)
y 2 =2px
если это уравнение принимает вид
y 2 =-2px
тогда ветви параболы направлены влево.
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Уравнение директрисы DD’
если поменять местами оси между собой, тогда
и график тогда будет выглядеть следующим образом (ветви направлены вверх)
Если в правой части уравнения отрицательный знак
x 2 = -2py
, то ветви параболы направлены вниз.
показывает смещение вершины параболы в точку ( x0 ; y0 )
Парабола относится к кривой второго порядка.
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Квадратичная функция. Построение параболы
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:ОГЭ 2022. Математика. Задание 11. Подробный разбор. Квадратичная функция Как отличать.Скачать

Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Видео:Уравнение параболы #алгебра #графики #парабола #репетиторСкачать

Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:
x
y
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x
y
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Видео:Как определить уравнение параболы по графику?Скачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.
D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>
Видео:Как строить параболу? | TutorOnlineСкачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>
Видео:Построение параболыСкачать

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Уравнение ветви параболы направленной вправо
Установите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
| А | Б | В |
Решение . Определим вид графика каждой из функций.
1) — уравнение параболы, ветви которой направленны вверх.
2) — уравнение прямой.
3) — уравнение верхней ветви параболы, направленной вправо.
4) — уравнение гиперболы.
Тем самым найдено соответствие: A — 1, Б — 4, В — 2.
График какой из приведенных ниже функций изображен на рисунке?

| 1) | 2) | 3) | 4) |
Решение . Ветви изображённой на рисунке параболы направленны вверх, а абсцисса вершины отрицательна. Следовательно, данному графику могут соответствовать функции или
Выделим полный квадрат в обоих выражениях:
Графику соответствует вариант под номером 3.
Приведем другое решение.
Ветви изображённой на рисунке параболы направленны вверх, а абсцисса вершины отрицательна. Следовательно, данному графику могут соответствовать функции или
Найдем координаты вершин параболы:
Формула 1:
Формула 3:
Следовательно, графику соответствует вариант под номером 3.
На одном из рисунков изображен график функции . Укажите номер этого рисунка.
Решение . Коэффициент , поэтому ветви параболы направлены вверх. Абсцисса вершины параболы равна:
Правильный вариант ответа указан под номером 1.
На одном из рисунков изображена парабола. Укажите номер этого рисунка.
Решение . Парабола изображена на рисунке 1.
Правильный ответ указан под номером 1.
График какой из приведенных ниже функций изображен на рисунке?
Решение . Изображённая на рисунке гипербола расположена в первой и третьей четвертях, следовательно, данному графику могут соответсвовать функции или
При
ордината функции на графике равна 5, следовательно, это график функции
На одном из рисунков изображен график функции . Укажите номер этого рисунка.
Решение . График функции — парабола. Определим тип каждого графика функции.
1) На первом рисунке изображена линейная функция.
2) На втором рисунке изображена логарифмическая функция.
3) На третьем рисунке изображена парабола.
4) На четвёртом рисунке изображена гипербола.
На одном из рисунков изображен график функции . Укажите номер этого рисунка.
| 1) | 2) |
| 3) | 4) |
Решение . График функции — гипербола. Определим тип каждого графика функции.
1) На первом рисунке изображена линейная функция.
2) На втором рисунке изображена парабола.
3) на третьем рисунке изображена показательная функция.
4) На четвёртом рисунке изображена гипербола.
На одном из рисунков изображена гипербола. Укажите номер этого рисунка.
Решение . Гипербола изображена на рисунке 2.
Установите соответствие между графиками функций и формулами, которые их задают.
| А) | Б) | В) | |||||||||||||||||
| 1) | 2) | 3) | 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение . Определим вид графика каждой из функций.
1) — уравнение прямой.
2) — уравнение гиперболы.
3) — уравнение параболы, ветви которой направленны вниз.
4) — уравнение верхней ветви параболы, направленной вправо.
Установите соответствие между графиками функций и формулами, которые их задают.
| А) | Б) | В) | |||||||
| 1) | 2) | 3) | 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение . Определим вид графика каждой из функций.
1) — уравнение гиперболы.
2) — уравнение параболы, ветви которой направленны вверх.
3) — уравнение прямой.
4) — уравнение параболы, ветви которой направленны вниз.
Установите соответствие между функциями и их графиками.
А)
Б)
В)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение . Напомним, что если парабола задана уравнением , то: при
то ветви параболы направлены вверх, а при
— вниз; абсцисса вершины параболы вычисляется по формуле
парабола пересекает ось Oy в точке с.
Уравнение задает параболу, ветви которой направлены вверх, абсцисса вершины равна
, она пересекает ось ординат в точке 0. Ее график изображен на рисунке 4).
Уравнение задает параболу, ветви которой направлены вверх, абсцисса вершины равна
, она пересекает ось ординат в точке 0. Ее график изображен на рисунке 1).
Уравнение задает параболу, ветви которой направлены вниз, абсцисса вершины равна
, она пересекает ось ординат в точке 0. Ее график изображен на рисунке 3).
Тем самым, искомое соответствие: А—4, Б—1, В—3.
📺 Видео
ОГЭ по математике.5 задание. ПараболаСкачать

НЕРАВЕНСТВА И ПАРАБОЛА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Квадратичная функция за 5 минутСкачать

Растяжение и сдвиги графика параболы / квадратичная функцияСкачать

Параболы. ОГЭ математика задача 5 (тип 3) 🔴Скачать

ОБЪЯСНЕНИЕ ГРАФИКА ПАРАБОЛЫ 😉 ЧАСТЬ I #shorts #егэ #огэ #математика #процентыСкачать

Как найти вершину параболы?Скачать

ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать

Квадратичная функция и ее график. 8 класс.Скачать

Как написать уравнение параболы с помощью графикаСкачать