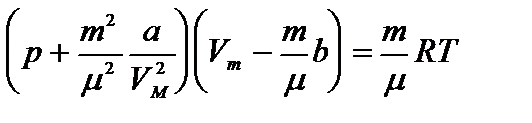Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873).
Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864)
постоянная b учитывает собственный мольный объем молекул.
При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления 

(p + 
Ван-дер-Ваальс в 1873 г. дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:
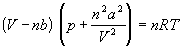
или для одного моля
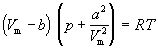
Значения постоянных Ван-дер-Ваальса a и b, которые зависят от природы газа, но не зависят от температуры, приведены в таблице 1.3.
Таблица 1.3. Постоянные Ван-дер-Ваальса для различных газов
| Газ | a, л 2 *бар* моль -2 | b,см 3 * моль -1 | Газ | a, л 2 * бар* моль -2 | b, см 3 * моль -1 |
| He | 0,03457 | 23,70 | NO | 1,358 | 27,89 |
| Ne | 0,2135 | 17,09 | NO2 | 5,354 | 44,24 |
| Ar | 1,363 | 32,19 | H2O | 5,536 | 30,49 |
| Kr | 2,349 | 39,78 | H2S | 4,490 | 42,87 |
| Xe | 4,250 | 51,05 | NH3 | 4,225 | 37,07 |
| H2 | 0,2476 | 26,61 | SO2 | 6,803 | 56,36 |
| N2 | 1,408 | 39,13 | CH4 | 2,283 | 42,78 |
| O2 | 1,378 | 31,83 | C2H4 | 4,530 | 5,714 |
| Cl2 | 6,579 | 56,22 | C2H6 | 5,562 | 63,80 |
| CO | 1,505 | 39,85 | C3H8 | 8,779 | 84,45 |
| CO2 | 3,640 | 42,67 | C6H6 | 18,24 | 115,4 |
Уравнение (1.6) можно переписать так, чтобы выразить в явном виде давление
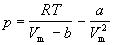
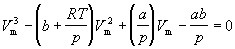
Уравнение (1.8) содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение (1.8) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.
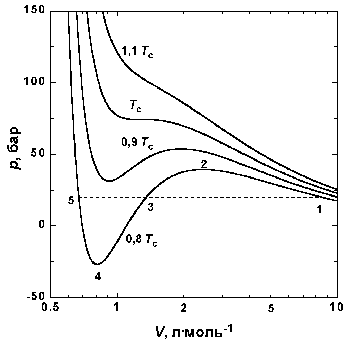 |
| Рис.1.4 Изотермы Ван-дер-Ваальса для СО2 |
На рис. 1.4 (стр. 7) приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода (значения констант a и b взяты из табл. 1.3). Из рисунка видно, что при температурах ниже критической (31,04 °С) вместо горизонтальных прямых, соответствующих равновесию жидкости и пара, получаются волнообразные кривые 12345 с тремя действительными корнями, из которых только два, 1 и 5, физически осуществимы. Третий корень (точка 3) физически не реален, поскольку находится на участке кривой 234, противоречащем условию стабильности термодинамической системы 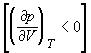
Согласно правилу Максвелла (the Maxwell construction), которое имеет теоретическое обоснование, для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо кривой 12345 провести горизонтальную прямую 15 так, чтобы площади 1231 и 3453 были равны. Тогда ордината прямой 15 будет равна давлению насыщенного пара, а абсциссы точек 1 и 5 – мольным объемам пара и жидкости при данной температуре.
По мере повышения температуры все три корня сближаются, и при критической температуре Tc все три корня становятся равными. В критической точке изотерма Ван-дер-Ваальса имеет точку перегиба [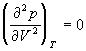
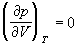
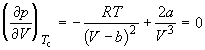
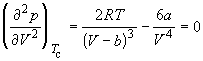
Совместное решение этих уравнений дает:
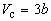
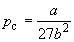
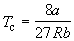
что позволяет определять константы уравнения Ван-дер-Ваальса из критических параметров газа. Соответственно, согласно уравнению Ван-дер-Ваальса, критический фактор сжимаемости Zc для всех газов должен быть равен
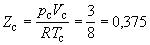
Из таблицы 1.2 видно, что хотя значение Zc для реальных газов приблизительно постоянно (0,27 – 0,30 для неполярных молекул), оно все же заметно меньше вытекающего из уравнения Ван-дер-Ваальса. Для полярных молекул наблюдается еще большее расхождение.
Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:
1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;
2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния (см. ниже);
3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме (см. 1.1, 1.2).
Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения (1.5) предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло (см. табл. 1.4).


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Видео:Уравнение Ван дер ВаальсаСкачать

Реальные газы. Уравнение Ван-дер-Ваальса. Критическое состояние.
Реальным называется газ, между молекулами которого действуют силы межмолекулярного взаимодействия, состоящие из сил притяжения и сил отталкивания.
Для получения уравнения состояния реального газа необходимо учесть собственный объем молекул и энергию взаимодействия молекул на расстоянии. Наличие собственного объема молекул приводит к уменьшению объема, предоставленного молекулам, на некоторую величину. Силы притяжения между молекулами газа вызывают уменьшение давления молекул газа на стенки сосуда на некоторую величину рi.
Это уравнение может получено путем соответствующего изменения уравнения Менделеева-Клапейрона путем внесения в него поправок.
Уравнение состояния реального газа (уравнение Ван-дер-Ваальса) для одного моля имеет вид:
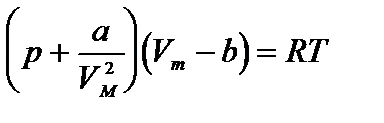
где р — давление, оказываемое на стенки сосуда, VМ – объем одного моля газа, а и b — постоянные Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем. Поправка 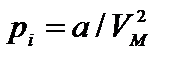
b= 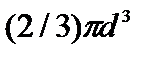
Уравнение Ван-дер-Ваальса для произвольной массы газа имеет вид:
Уравнение Ван-дер-Ваальса позволяет построить теоретические изотермы реального газа и сравнить их с изотермами идеального газа и экспериментальными изотермами реального газа.
Уравнение Ван-дер-Ваальса после нескольких преобразований можно записать в виде:
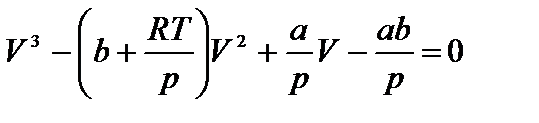
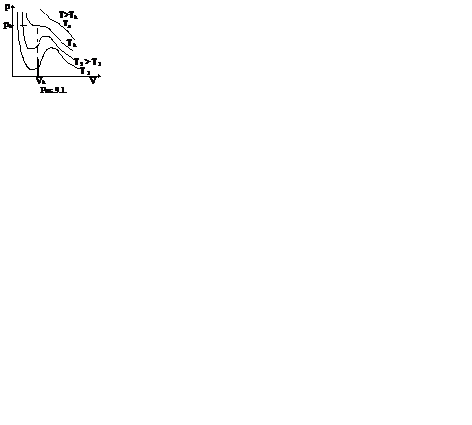
Это уравнение третьей степени относительно V. Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный и два мнимых.
Первому случаю соответствуют изотермы при низких температурах – кривые для Т1 и Т2 (рис.9.1.) Второму случаю изотермы при высоких температурах (одно значение объема V отвечает одному значению давления р), то есть любая изотерма начиная от изотермы для Тк.
Совпадение изотерм идеального и реального газа наблюдается при малых давлениях и больших объемах (так как при этих условиях газ можно считать идеальным). Для семейства изотерм Ван-дер-Ваальса характерно так называемой критической изотермы (при температуре Тк) имеющий точку перегиба при некотором давлении рк и объеме Vк; при Т>Тк все изотермы идут монотонно, при Т
Уравнение Ван-дер-Ваальса описывает не только свойства газов и паров, но и жидкостей. Анализ изотерм реального газа показывает, что превращение реального газа в жидкость возможно только при температурах, меньших критической, и при соответствующих давлениях.
Дата добавления: 2015-04-01 ; просмотров: 18358 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Лекция 10 Реальные газы. Уравнение Ван-дер-Ваальса
- Любовь Кулько 4 лет назад Просмотров:
1 Лекция 10 Реальные газы. Уравнение Ван-дер-Ваальса 1. Силы межмолекулярного взаимодействия 2. Уравнение Ван-дер-Ваальса 3. Экспериментальные изотермы и изотермы Ван-дер-Ваальса. Критические состояния 4. Приведенное уравнение Ван-дер-Ваальса 5. Внутренняя энергия газа Ван-дер-Ваальса 6. Эффект Джоуля-Томсона 7. Методы сжижения газа 1. Силы межмолекулярного взаимодействия Законы идеальных газов, вытекающие из молекулярно-кинетических представлений, достаточно хорошо подтверждаются на опыте в том случае, если давление газа мало и температура его не слишком низка. При повышении давления поведение реальных газов отклоняется от поведения газов идеальных. На рисунке 10.1 показано, как изменяется произведение давления реального газа на занимаемый им объем при увеличении давления. Для идеального газа подобная зависимость выражается прямой линией, параллельной оси абсцисс. Рассматривая график (рис. 10.1), мы убеждаемся в том, что реальный газ при увеличении давления первоначально сжимается больше, чем это следует из уравнения идеальных газов, так что произведение pv уменьшается с возрастанием давления. При дальнейшем увеличении давления начинают сказываться какие-то иные свойства молекул реальных газов, в силу которых произведение pv перестает убывать. Если продолжать газ сжимать, то оно возрастает, делаясь больше величины, следующей из теории. Рисунок 10.1 Диаграммы состояния идеального и реального (О 2) газов Причины подобных отклонений легко понять. Большую сжимаемость реального газа по сравнению с газом идеальным обусловливают силы межмолекулярного взаимодействия (потенциал Ленард Джонса, см. лекцию 1). Молекулярное сцепление приводит к возникновению как бы добавочного давления возрастающего при возрастании плотности газа. Наблюдаемое при высоких давлениях уменьшение сжимаемости и соответствующее возрастание произведения pv объясняется тем, что реальные молекулы не являются материальными точками, а обладают некоторым конечным объемом. Учет объема молекул эквивалентен учету сил отталкивания, проявляющихся в тех случаях, когда расстояние между молекулами мало. Выше было показано, что давление газа зависит от числа ударов молекул о стенку сосуда за 1 секунду. Это число увеличивается, если при расчете принять во внимание присущий молекулам объем. Действительно, при центральном соударении какой-либо молекулы с другой молекулой количество движения, которым обладает первая молекула, переносится практически мгновенно на отрезок, равный диаметру молекулы (рисунок 10.2, а). В результате этого уменьшается промежуток времени,
2 разделяющий два последующих удара молекулы о стенку сосуда, и, следовательно, увеличивается число ударов ее об эту стенку за одну секунду. По мере увеличения давления возрастает плотность газа, а вместе с ней возрастает влияние собственного объема молекул газ оказывает большее сопротивление сжатию, чем это следует из уравнения идеальных газов (уравнения Менделеева Клапейрона). Рисунок 10.2 Модели соударения молекул в реальном газе Следует заметить, что на необходимость учитывать при расчете давления сильно сжатого газа собственный объем молекул указывал еще Ломоносов. 2 Уравнение Ван-дер-Ваальса и другие уравнения идеального газа Уравнение состояния реального газа, в котором приняты во внимание обе причины, вызывающие отклонения его свойств от свойств идеальных газов, было предложено впервые голландским физиком Ван-дер-Ваальсом ( ) и носит его имя. Уравнение Ван-дер- Ваальса отличается от уравнения Клапейрона наличием двух поправочных членов, один из которых учитывает влияние собственного объема молекул, а другой влияние сил молекулярного притяжения. Для того чтобы учесть влияние собственного объема молекул, обратим внимание на то, что при увеличении давления Р стремится к нулю, а объем реального газа при тех же условиях к некоторой предельной величине b. Следовательно, для того чтобы в уравнении состояния идеальных газов учесть влияние собственного объема молекул, необходимо заменить в нем величину V разностью (V b). Таким образом, уравнение состояния, учитывающее собственный объем молекул, будет иметь вид: p (V b) = R T (10.1) Теоретический расчет величины b сложен. В простейшем случае, если считать молекулы газа твердыми шариками с радиусом r и предположить при этом, что в газе происходят только двойные соударения молекул, то можно показать (учитывая, что передача импульса происходит в пределах расстоянии от 0 до 2r), что b равно учетверенному собственному объёму молекул:
3 4 3 b 4N A r 3 Если газ сжат настолько сильно, что в нем наряду с двойными соударениями наблюдаются тройные и более сложные соударения молекул, величина поправочного члена, учитывающего влияние собственного объема молекул, будет иной. Величина поправки к давлению, обусловленная молекулярным притяжением, строго говоря, должна зависеть от плотности газа и от закона, согласно которому изменяется сила, действующая между молекулами при изменении расстояния между ними. Однако при выводе уравнения Ван-дер-Ваальса последняя зависимость не принимается во внимание. Это оказывается возможным сделать, если, учитывая подвижность молекул, предположить, что все положения какой-либо молекулы в мысленно выделенном небольшом объеме газа равновероятны. В этом случае взаимодействие любой молекулы в одном из выделенных объемов с молекулами такого же соседнего объема будет равно средней величине взаимодействия ее при всех возможных положениях, занимаемых ею относительно соседнего объема. Сказанное будет справедливо для всех молекул как в первом, так и во втором объеме. Если теперь мысленно провести плоскость внутри газа (рисунок 35), то Рисунок 10.3 Схема взаимодействия молекул в двух соседних объёмах молекулы, находящиеся в малом объеме справа от этой плоскости, будут притягиваться молекулами, находящимися в таком же объеме слева от нее, с одинаковой для всех молекул средней силой. Необходимо отметить, что, строго говоря, это предположение может быть оправдано только в случае, если оно относится к разреженному газу. На рисунке 10.3, а) в каждом из рассматриваемых объемов находится по одной молекуле. При увеличении плотности газа в два раза число молекул в каждом из объемов удваивается (рисунок 10.3, б), а сила, с которой один объем притягивает другой учетверяется. При увеличении плотности газа в три раза (рисунок 10.3, в) сила притяжения увеличится в 9 раз. Из рассмотренного примера следует, что обусловленное молекулярным притяжением добавочное, или как его называют, внутреннее давление рг в реальных газах возрастает прямо пропорционально квадрату плотности газа или, другими словами, обратно пропорционально квадрату молекулярного объема V, т. е. a p (10.2) 2 V где a постоянная величина, различная для различных газов, зависящая от интенсивности молекулярных взаимодействий. Внутреннее давление не фиксируется манометром (уменьшает давление на стенку) и потому должно добавляться к манометрическому давлению.
4 Учтя, таким образом, влияние на поведение газов собственного объема молекул и сил, действующих между ними, Ван-дер-Ваальс предложил записать уравнение состояния реальных газов в следующем виде: a p V b R T V 2 (10.3) Опыт показывает, при повышении давления уравнение Ван-дер-Ваальса лучше передает свойства реального газа, нежели уравнение Клапейрона. Внутреннее давление, играющее роль поправочного члена, когда внешнее давление невелико, увеличивается при возрастании последнего и может при определенных условиях существенно влиять на свойства газов. В приведенной выше форме уравнение Ван-дер-Ваальса (10.3) относится к одному молю газа, так что входящая в него величина объема газа это молярный объем. При желании использовать написанное уравнение применительно к т килограммам вещества необходимо помнить, что значения постоянных а и b в этом случае будут иными. Если молярная масса газа и если желательно сохранить значения постоянных а и b, определенных для одного моля вещества, то уравнение Ван-дер-Ваальса следует записывать так: 2 a p V b R T (10.4) 2 V В этом уравнении V объем, занимаемый т килограммами газа. Величины а и b для газов можно найти в справочный таблицах (постоянные Ван дер Ваальса). В заключение следует подчеркнуть приближенный характер уравнения Ван-дер- Ваальса, которое, хотя и лучше передает поведение реальных газов, чем уравнение Клапейрона, все же мало пригодно для точных расчетов. Вычисленные с помощью уравнения Ван-дер-Ваальса значения давления газа достаточно точно совпадают с опытом лишь при относительно высоких температурах и только в некотором интервале давлений. Этим объясняются непрерывные поиски более совершенных уравнений, которых в настоящее время известно более 150. При малых давлениях и соответственно больших значениях молекулярного объема V можно пренебречь в уравнении Ван-дер-Ваальса поправкой, в силу ее малости по сравнению с р, и поправкой b по сравнению с молекулярным объемом V. Уравнение Ван-дер-Ваальса при этих условиях переходит в уравнение идеальных газов. 3 Экспериментальные изотермы и изотермы Ван-дер-Ваальса. Критические состояния Уравнение Ван-дер-Ваальса алгебраическое уравнение третьей степени относительно объема. Раскрыв скобки и расположив члены уравнения Ван-дер-Ваальса по убывающим степеням объема, можно записать последнее в следующем виде: 3 RT 2 a ab V b V V 0 (10.5) p p p На рисунке 10.4 изображена подобная зависимость для того случая, когда температура газа не слишком высока. Вдоль оси абсцисс отложен объем, вдоль оси ординат давление газа. Кривая, которая изображена на графике, рассчитана при постоянной температуре и, следовательно, является изотермой. Для того чтобы проанализировать физический смысл отдельных участков полученной изотермы, рассмотрим мысленный опыт, схема которого изображена на том же рисунке. Параллельно оси абсцисс
5 расположена толстостенная стеклянная трубка, наполненная углекислотой и закрытая с правого конца поршнем. К левому концу трубки прикреплен ртутный манометр. Положение поршня непосредственно указывает объем, занимаемый газом. Давление газа регистрируется по положению уровня ртути в манометре. Пересечение прямых, одна из которых параллельна оси абсцисс на уровне ртути в Рисунок 10.4 Схема мысленного опыта, проводимого над реальным газом манометре, а вторая параллельна оси ординат и указывает положение поршня в трубке, наполненной газом, происходит в точке С, изображающей на расположенной выше диаграмме определенное состояние газа. Перемещая поршень и отмечая указанным способом состояния газа, можно с помощью подобного прибора выяснить, насколько правильно передает уравнение Ван-дер-Ваальса поведение реального газа. Результаты подобного опыта изображены на рисунке 10.4 пунктирной линией. Сопоставляя рассчитанную теоретически кривую BFAC с кривой, построенной на основании опыта, мы убеждаемся в том, что если объем газа не слишком мал, то уравнение Ван-дер-Ваальса удовлетворительно согласуется с опытом. Качественное согласие с опытом наблюдается до тех пор, пока давление в трубке не сделается равным давлению насыщенного пара углекислоты, а объем V объему VH занимаемому насыщенным паром при данной температуре. При заданной температуре давление насыщенного пара является величиной постоянной, и потому дальнейшее уменьшение объема не влечет за собой увеличения давления. Уменьшение объема, занятого насыщенным паром вещества, вызывает конденсацию, т. е. переход вещества из парообразного состояния в жидкое. На экспериментальной изотерме процессу конденсации соответствует прямолинейный участок, параллельный оси абсцисс. Конденсация заканчивается в тот момент, когда все вещество превращается в жидкость и объем его делается равным молекулярному объему жидкости Vж. Поскольку жидкости обладают малой сжимаемостью, дальнейшее уменьшение объема вызывает значительное увеличение давления. Качественно это согласуется с полученными на основании уравнения Ван-дер-Ваальса результатами. Таким образом, в качественном отношении различие между теоретическими и экспериментальными изотермами реальных газов при относительно низких температурах сводится к тому, что s-образный участок теоретических изотерм заменяется у кривых, полученных экспериментально, горизонтальной прямой. Если подвергаемый сжатию газ тщательно очистить от пыли, то можно наблюдать задержку возникновения конденсации, в результате которой удается сжать газ до объема, меньшего, чем объем насыщенного пара, и, соответственно, до давления, большего, чем
6 давление насыщенного пара при данной температуре. Таким способом можно на опыте воспроизвести качественно участок АС изотермы Ван-дер-Ваальса и тем самым выяснить его физический смысл. Очевидно, этот участок изотермы соответствует пересыщенному пару вещества. Это состояние неустойчиво, в веществе спонтанно возникает конденсация, при которой давление скачкообразно падает до давления насыщенного пара (подобный процесс на рисунке 10.4 изображен стрелкой). Точно так же при изотермическом увеличении объема сжатой жидкости экспериментально можно наблюдать задержку образования паровой фазы, несмотря на то что объем, занимаемый жидкостью, превышает ее молекулярный объем. Давление в системе при этом будет ниже соответствующего данной температуре давления насыщенного пара жидкости. Задержка возникновения паровой фазы позволяет экспериментально воспроизвести в качественном согласии с теорией участок BF изотермы Ван-дер-Ваальса. Эта часть теоретической изотермы соответствует неустойчивому состоянию растянутой жидкости. Это состояние принято называть состоянием перегретой жидкости в том смысле, что при данном значении молекулярного объема и температуры часть жидкости должна была бы находиться в парообразном состоянии, в то время как на опыте паровая фаза отсутствует. Участок AF изотермы Ван-дер-Ваальса соответствует совершенно неустойчивому состоянию вещества, при котором давление в системе должно было бы уменьшаться при уменьшении объема системы и расти при его увеличении. На опыте это состояние не реализуется. Таким образом, уравнение Ван-дер-Ваальса качественно правильно передает изменение давления вещества при изменении объема как в случае пара, так и в случае жидкости. Уравнение предсказывает наличие неустойчивых состояний, а именно состояния перегретого пара и состояния растянутой жидкости. Однако теория Вандер-Ваальса не учитывает возможности одновременного присутствия вещества в парообразном и жидком состояниях. Если изобразить на графике изотермы Ван-дер-Ваальса, рассчитанные теоретически при разных значениях температуры, то получится семейство кривых, подобное изображенному на рисунке Рисунок 10.5 Изотермы Ван дер Ваальса Как можно убедиться, при повышении температуры s-образный участок изотермы Ван-дер-Ваальса уменьшается, другими словами, уменьшается разница между
7 молекулярными объемами насыщенного пара и жидкости. При некоторой температуре Tk, называемой критической температурой, s-образный участок изотермы исчезает. На соответствующей изотерме, которую называют критической, вместо s-образного участка наблюдается точка перегиба К, которая называется критической точкой. При более высоких температурах изотермы Ван-дер-Ваальса напоминают изотермы идеальных газов. Экспериментально поведение реальных газов было изучено Эндрьюсом ( ), найденные им изотермы изображены на рисунке 10.6 Рисунок 10.6 Области существования вещества в различных состояниях Если соединить между собой правые концы горизонтальных участков экспериментальных изотерм, то полученная кривая будет изображать изменение с температурой молекулярного объема насыщенного пара вещества. Молекулярный объем насыщенного пара уменьшается с увеличением температуры вплоть до критической температуры. Соединив между собой левые концы горизонтальных участков опытных изотерм, получим параболическую кривую, изображающую зависимость от температуры молекулярного объема жидкости, который увеличивается с возрастанием температуры. При критической температуре молекулярный объем жидкости делается равным молекулярному объему пара. Очевидно, что выше критической температуры вещество не может находиться в жидком состоянии. На эту особенность вещества впервые указал Д. И. М е н д е леев ( ), который назвал критическую температуру вещества температурой абсолютного кипения. Критическая изотерма и проведенные параболические кривые делят диаграмму состояния на несколько областей (рисунок 10.6). Область Ж, расположенная между осью ординат, участком АК критической изотермы и левой ветвью параболы ВК, соответствует тем значениям объема и давления, при которых вещество находится в жидком состоянии. Область П, ограниченная участком KA критической изотермы и правой ветвью параболы КС, выделяет значения давления и объема, соответствующие веществу в парообразном состоянии. Выше критической изотермы расположена область Г вещества в газообразном состоянии. Наконец, область, ограниченная осью абсцисс и параболой ВКС, соответствует одновременному присутствию вещества в жидком и парообразном состояниях. Это область, в которой вещество находится одновременно в двух различных агрегатных состояниях, или гетерогенная область. Таким образом, сжатие вещества при температуре ниже критической вызывает при определенном давлении его конденсацию, в то время как любое сжатие вещества при температурах выше критической не вызывает конденсации. При температурах выше критической, увеличивая давление, нельзя превратить газообразное вещество в жидкое.
8 Теория Ван-дер-Ваальса указывает на возможность непрерывного перехода вещества из жидкого состояния в газообразное без распадения вещества на две фазы. Непрерывный переход из жидкого состояния в газообразное изображен на рисунке 10.6 стрелками. Отрезки ab и bе изображают нагрев вещества до критической температуры. Давление в системе при этом возрастает выше критического давления. Дальнейшее изменение состояния вещества может заключаться или в изотермическом расширении, при котором давление уменьшается до критического и жидкость в критической точке превращается в пар, или же в изобарном нагревании, при котором вещество превращается в газ при давлении выше критического. Естественно, что возможен и обратный непрерывный, т. е. не сопровождающийся распадением вещества на две фазы, переход из газообразного состояния в жидкое. Этот переход показан на диаграмме стрелками a1b1 и b1e1. 4 Приведенное уравнение Ван-дер-Ваальса Соответствующие критической точке значения давления pk, объема Vk и температуры Tk называют: критическим давлением, критическим объемом и критической температурой вещества. Критические параметры pk, Vk и Tk являются индивидуальными характеристиками вещества, зависящими от свойств его молекул. Уравнение Ван-дер-Ваальса позволяет установить однозначную связь между входящими в это уравнение постоянными а и b и критическими параметрами вещества. Как всякое уравнение 3-й степени, уравнение Ван-дер-Ваальса можно представить в виде: V V V V V 0 V (10.6) в котором V1 V2 и V3 являются тремя корнями уравнения, як При критической температуре Vi = V2 = Va = Vk и, следовательно: Это уравнение должно быть тождественно с уравнением Ван-дер-Ваальса, написанным для критической изотермы: Написанные уравнения будут тождественными в том случае, если будут равны коэффициенты у членов, содержащих одинаковые степени V. Из этого условия следуют соотношения: (88) (87) пользуясь которыми, можно найти следующие зависимости между критическими параметрами вещества и соответствующими значениями постоянных в уравнении Ван-дер- Ваальса: (89) или (90) Если подставить найденные значения постоянных а, b’u R в уравнение Ван-дер- Ваальса и условиться измерять давление, объем и температуру для каждого вещества
9 отношением этих величин к их критическим значениям, а именно: (91) то уравнение состояния примет следующий вид: (92) т. е. оно не будет содержать произвольных постоянных 1. Определенные, как это сделано выше, величины давления, объема, температуры называют: приведенным давлением, приведенным объемом и приведенной температуроq. Уравнение Ван-дер-Ваальса, в котором используются приведенные величины, называется п р и в е д е н н ы м у р а в н е н и е м В а н — д е р — В а а л ь с а. Если два или несколько веществ нахо- 1 Написанное уравнение содержит определяемые опытным путем постоянные в с к р ы т о й ф о р м е. Этими постоянными являются критические параметры вещества. дятся в состояниях, при которых приведенные значения двух каких-либо параметров состояния у них одинаковы, то одинаковы приведенные значения и третьего параметра. В этом случае говорят, что вещества находятся в с о о т в е т с т в е н н ы х с о с т о я ниях. 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ Силы молекулярного притяжения имеют сложную природу, хотя в конечном счете все они сводятся к взаимодействию электрических зарядов. Как известно, атомы, входящие в состав молекул, состоят из положительно заряженных ядер, окруженных большим или меньшим количеством быстро вращающихся электронов. Хотя в сумме положительные заряды атомных ядер в молекулах равны суммарному отрицательному заряду электронов, т. е. в целом молекулы электрически нейтральны, однако пространственно положительные и отрицательные заряды не совпадают. В настоящее время достоверно известно, что существуют молекулы, у которыхfuc. ёу. строение электрические заряды распределены немолекулы воды. равномерно. У подобной молекулы водной части оказываются преобладающими положительные заряды, а в другой отрицательные. Дваравных разноименных электрических заряда, разделенные некоторым расстоянием, образуют э л е к т р и ч е с к и й д и п о л ь. Поэтому молекулы с несимметричным распределением электрических зарядов называют дипольными, или п о л я р н ы м и, молекулами. Примером полярной молекулы может служить молекула воды (рис. 39). Та часть молекулы, в которой расположен атом кислорода, заряжена преимущественно отрицательно. Дипольные молекулы всегда стремятся ориентироваться друг относительно друга так, чтобы против положительного полюса одной молекулы располагался бы отрицательный полюс другой. Это обусловлено электрическим взаимодействием разноименных полюсов. Несмотря на то что тепловое движение молекул нарушает подобную ориентацию, все же она является преимущественной, в результате чего между дипольными молекулами возникают силы притяжения. Поскольку этот вид взаимодействия молекул связан с их взаимной ориентацией, его называют о р и е н т а ц и о н н ы м в з а и м о д е й с т в и е м, или о р и е н т а ц и о н н ы м эфф е к т о м. Ориентационный эффект одно из слагаемых вандер-ваальсовых сил.
10 Однако это взаимодействие не может во всех случаях объяснить молекулярное притяжение. Наряду с полярными молекулами существуют молекулы с симметричным расположением электрических зарядов, не имеющие дипольного момента. Такие молекулы называют н е п о л я р н ы м и. Неполярны молекулы двухатомных газов: азота, кислорода, водорода, молекулы углекислоты, пары бензола и многие другие. Симметричность электрических зарядов в неполярных молекулах легко нарушается, если подобная молекула ‘оказывается вблизи полярной молекулы или иона. В этих условиях у неполярной молекулы возникает дипольный момент, называемый и н д у ц и р о в а н н ы м д и п о л ь н ы м м о м е н т о м. Взаимодействие индуцированных дипольных моментов, возникших в молекулах, вызывает в свою очередь возникновение молекулярного притяжения. Это взаимодействие называют инд у к ц и о н н ы м э ф ф е к т о м. Индукционный эффект незначителен и не может объяснить наблюдаемую на опыте величину ван-дер-ваальсовых сил. За редким исключением молекул с большим дипольным моментом, основной причиной возникновения молекулярного притяжения являются взаимодействия так называемых м г н о в е н н ы х, или о с ц и л л и р у ю щ и х д и п о л е й. Входящие в состав молекулы положительно заряженные ядра атомов и отрицательно заряженные электроны совершают своего рода колебания друг относительно друга. Таким образом, мгновенная картина даже неполярной молекулы обнаруживает различные смещения ядер и электронов. Величина этого смещения изменяется во времени так, что молекулы вне зависимости от того, полярны они или нет, ведут себя как периодически возникающие (осциллирующие) диполи. При сближении молекул мгновенные диполи вызывают появление в соседних молекулах согласованно изменяющихся индуцированных диполей, взаимодействие с которыми и приводит к возникновению молекулярного притяжения. Т а б л и ц а 11 Соотношение между различными составляющими молекулярных сил (в /0) Вещество Аммиак. Хлористый водород.. О риентационный И ндукционный Ди сперсионный Те же колебания электрических зарядов в молекулах вызывают различное преломление лучей света с разной длиной волны, называемое дисперсией и проявляющееся в возникновении оптического спектра. По этой причине силы, обусловленные взаимодействием мгновенных диполей, называют д и с п е р с и о н н ы м и с и л а м и. В реальных газах с неполярными молекулами ван-дер-ваальсовые силы практически полностью обусловлены дисперсионным взаимодействием. В таблице 11 приведены относительные величины ориентацион-ного, индукционного и дисперсионного взаимодействия для некоторых молекул. 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА Внутренняя энергия идеального газа, поскольку в нем отсутствуют молекулярные взаимодействия, представляет собой кинетическую энергию движения молекул, которая зависит от температуры газа, но не зависит от занимаемого газом объема. В реальных газах нельзя пренебрегать взаимодействием молекул, и потому внутренняя энергия реального газа находится суммированием кинетической энергии движения молекул Ek и потенциальной энергии их взаимодействия Ер:
11 II ‘ F -U F ^реатьн. газа *-k
р ш Потенциальная энергия молекулярного взаимодействия зависит от взаимного расположения молекул и потому должна изменяться при изменении объема газа. Если исключить обмен энергией между газом и внешней средой, то сумма присущей молекулам газа кинетической и потенциальной энергий должна оставаться постоянной и, следовательно, изменение одного из видов энергии должно компенсироваться противоположным изменением второго вида энергии: АЕр = — AEk. Если учитывать только притяжение молекул, то их потенциальная энергия должна возрастать при удалении молекул друг от друга, т. е. расширение реального газа при этих условиях должно сопровождаться уменьшением кинетической энергии его молекул. Поскольку же мерой средней кинетической энергии молекул газа служит его абсолютная температура, то при расширении газа, молекулы которого притягиваются друг к другу, температура его должна понижаться. Впервые подобный опыт удалось осуществить совместно Д. Д ж о у л ю ( ) и В. Т о м с о н у ( ). В опыте Джоуля Томсона для обнаружения изменения внутренней энергии реального газа при изменении объема газ заставляют расширяться через пористую перегородку (рис. 40), установленную в трубке, соединяющей сосуды А и В. Специальные насосы поддерживают в этих сосудах постоянные давления: в сосуде А давление plt а в сосуде В меньшее давление Рг- По обе стороны от пористой перегородки помещают термометры. Как показали опыты, Рис. 40. Схемы опыта Джоуля большинство газов, расши- Томсона. ряясь при комнатной температуре и не очень больших давлениях, охлаждается. Исключение составляет водород, который при этих условиях нагревается. Изменение температуры, сопровождающее расширение реального газа, получило название э ф ф е к т а Д ж о у л я Томсона. Охлаждение газа при расширении называют положительным эффектом Джоуля Томсона, нагревание отрицательным. Для того чтобы понять существование эффекта Джоуля Томсона разного знака, обратимся к графику, поясняющему отклонение поведения реального газа от газа идеального (рис. 41). Сплошными линиями на графике изображено изменение отношения произведения давления газа на занимаемый им объем к абсолютной температуре при изменении давления для трех различных температур Ти Т2, Ts, удовлетворяющих условию Ti 12 притяжения за счет присущей им кинетическойрм энергии. В результате при расширении газ будет охлаж- 91 даться, т. е. будет наблюдаться положительный эффект Джоуля Томсона. При более высокой температуре Т3, как это явствует из чертежа, преобладающее значение имеют силы отталкивания, учитываемые в уравнении Ван-дер-Ваальса поправочным членом Ь. Эти силы будут совершать работу при расширении реального газа и тем увеличивать кинетическую энергию молекул. В этом случае при расширении реального газа будет наблюдаться нагревание, т. е. отрицательный эффект Джоуля Томсона. При некоторой промежуточной температуре Тг влияние сил притяжения в точности компенсируется влиянием сил отталкивания и реальный газ ведет себя как газ идеальный, т. е. его расширение не сопровождается изменением температуры. Таким образом, при плавном изменении температуры от значения 7 до значения Та знак эффекта Джоуля Томсона изменяется с положительного на отрицательный. Это происходит при температуре, называемой т е м п е р а т у р о й и н в е р с и и. Для кислорода температура инверсии -[-790 С, для углекислоты -f-1800 C, однако для водорода температура инверсии 73 С. Водород будет охлаждаться при расширении только в том случае, если его температура ниже 73 С, в противном же случае при расширении он нагревается. Эффект Джоуля Томсона находит себе важное применение в технике при сжижении газов. 28. СЖИЖЕНИЕ ГАЗОВ Анализ уравнения Ван-дер-Ваальса показывает, что все вещества при понижении их температуры ниже критической могут быть превращены в жидкость простым увеличением давления. В таблице 12 приведены критические температуры и давления некоторых веществ. Крит Крит Вещест темп давл Вода 374, Бензол 288, ,7 Хлор 144,0 77,1 Углеки 31,1 73,9 Кислор 50,3 Азот 33,9 Водоро 13,0 Гелий 2,29» 267,9
💥 Видео
Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Уравнение Ван-дер-Ваальса и опыт Джоуля и ТомсонаСкачать

Урок 195. Изотермы реального газаСкачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

270. Силы Ван-дер-ВаальсаСкачать

Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

35. Реальные газыСкачать

Как жуки используют силы Ван-дер-Ваальса?Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

Сила Ван дер ВаальсаСкачать

1 3 Водородная связь Ван дер Ваальсовы силыСкачать

Силы Ван-дер-Ваальса (видео 1) | Силы межмолекулярного взаимодействия | ХимияСкачать

Кубический Ван-дер-ВаальсСкачать

Реальные газы и жидкости Сжижение метанаСкачать

Лекция №7 "Газ Ван-дер-Ваальса. Эффект Джоуля-Томсона" (Овчинкин В.А.)Скачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать