Уравнение ван дер поля решение

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

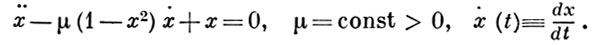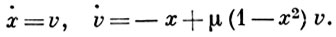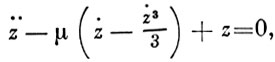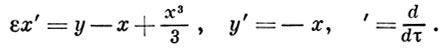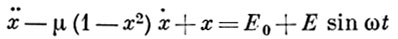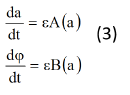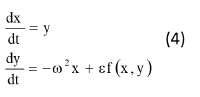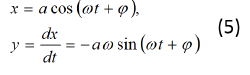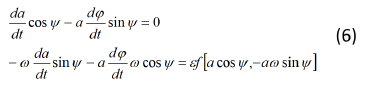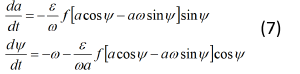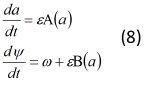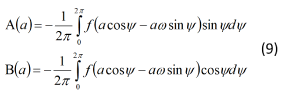
Метод медленно меняющихся амплитуд (метод Ван-дер-Поля)

Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Метод медленно меняющихся амплитуд (метод Ван-дер-Поля)

• Этот метод полезен, когда движение материальной системы описывается дифференциальным уравнением с малой нелинейностью. Х А х я i. 4. Где f x, i -нелинейная функция x и, А p-малый параметр. если f x, f 0, то уравнение 4 будет линейным I A x 0, общее решение которого, как известно х asln Ш А, х aAcos а а. В 1926 году Ван дер Поль предложил, что для малой нелинейности общее решение Формулы 4 и ее первая производная имеют внутренний индекс, соответствующий линейному уравнению 2×0. х грех т а, я Ак COS в т а, 5 Где амплитуда а и начальная фаза а-медленно меняющиеся функции времени а а 0, х х 0. Этот метод позже Л. И. Мандельштама и N. D.

Было продемонстрировано математически в исследовании папалекси. Мы видим, что это нелинейное дифференциальное уравнение 2-го порядка 4 эквивалентно 2 нелинейным дифференциальным уравнениям 1-го порядка. a j — asinij , ak cos , a — asinifi, ak cos , где вводится обозначение. Вместо этих точных уравнений было предложено закрепить приближение-уравнение, полученное из укороченного 6, заменив правую часть соответствующей средней величиной в диапазоне от 0 до 2, то есть правой стороной. 2р Если а 2 ф asinTf, аль cosxj з-рН, 7 2р a — a slnф cosФ sln 4 8 При вычислении правых интегралов этих приближенных нелинейных уравнений амплитуда a должна считаться постоянной.

При вычислении момента инерции однородного трехмерного твердого тела относительно некоторой оси выделяют в твердом теле-такой элементарный объем, момент инерции которого относительно соответствующей оси известен, либо легко может быть определен. Людмила Фирмаль

Интегралы дифференциальных уравнений свободных колебаний с малыми нелинейностями методом ван дер поля рекомендуется выполнять в следующем порядке 1 Создайте дифференциальное уравнение свободной вибрации и запишите его в виде 4. 2 взять x a sin f, x aAcosif и вычислить определенный интеграл 2-й 2-й Дж. Ф. грех доктора, Ак sovf sovf Ф, asinty, Ак cosф sinф ф При рассмотрении константы 3 Добавить результат предыдущего абзаца справа от укороченного уравнения ван дер поля 7 и 8. 4 интегрируйте уравнение 7 и вычислите полное интегрирование Ф, ст 5 присвоить полученные значения a t, Cj укороченному дифференциальному уравнению 8 и интегрировать его, вычисляя общий Интеграл a a f, Cb C9.

Подставляя полученные значения a t, Cj и a t, Cy Ca в уравнение 5, определить начальное условие заданного движения 0, x x0, I интегральная константа C 7 полученные значения Ci и Ca вычисляются в пунктах a A Z, Cj и a a т. е. если вы хотите добавить к нему значение, вам нужно добавить его в Cy Cg. 4 и 5 8 подставляя искомое уравнение движения О грехе А М Значения a t и a , полученные в предыдущем пункте. Задача 20.3.Решите задачу 20.2, используя метод медленного изменения амплитуды. Решение.

Напишите рассматриваемое дифференциальное уравнение 4 20.2 по форме Ф 2е р р 1 2 Найти решение в виде Формулы 1 и ее производных первого порядка Ф ж грех В а т, ф А А Т, потому что Т А я Джей 3 Где переменная амплитуда в 0 и переменная начальная фаза а 0 являются предметом последующего определения. Если сравнить уравнения 1 и 4, приведенные в обзоре теории, то в этом случае x p Ф. ф ф СР a sin , и P aAsozph аз nf, а A cos f a s1a f. 4 0 и 0, предварительное вычисление определенных интегралов 2р 2р м НП, aAco5p Софья 7п и J a81pf, aAco8p 81pf1 Ф 4 в предположении, что существует и величина а постоянна Ф грех Ф Ак со Ф соз ф ф А Й грех Ф со Ф Ыф 2л 2л J A sin , ak cos sin a J sin.

Если использовать подстановку sfnif z с первым интегралом b , а во 2-м Интеграле 5 с выражением sin ij — —soz2p at sob4p Второй Дж. Ф. Син Ф Ак со Ф соз Ф с ф 0 2л Ф А sin , Ак при cos sin — — Ла. 6 Вводя значение интеграла 6 в укороченное уравнение ван дер поля 7 и 8, приведенное в обзоре теории и рассматривая 2 а 0, д 7 Из первого выражения 7 е 0-ср. 8 Если вы присваиваете 8 2 — му выражению 7, то оно имеет вид a — AC .Когда вы интегрируете Подставляя результаты 8 и 9 в Формулу 3, можно найти -C,, 1n 4 1- C С, , 10 4.-4C1eo1 я л-ЛК с,. 11 В 10 0, p a0, 11 вводя t 0, p 0, получаем систему уравнений a0 ClsinC2l 0 ZrCj cos Sc.

• Если вы решите эту систему, у вас будет Ci a0, Ct n 2, если Cj 0, то решение системы будет потеряно вообще. Подставляя полученные значения Cx и Ca в 10, находим искомое уравнение для колебаний маятника. Ф conv convl 1 — 12 Как видно из 12, круговая частота p колебаний маятника, согласно его начальному угловому отклонению a0 — — ..И 13 Если мы решим уравнение 12 и результат задачи 20.2 21 способом, расширяющимся с малыми параметрами, мы увидим, что метод ван дер поля производит первый первичный член уравнения 21 задачи с несколько меньшим вычислительным весом. Оказывается, что размер циркулирующей частоты p, найденный двумя способами, одинаков см.

Уравнение в вопросе 20.2 13 и уравнение 20. Поэтому применение метода ван дер поля для определения первого приближения должно считаться целесообразным и эффективным. Задание 20.4.Материальная точка массы m движется вдоль оси x под действием упругих сил и сопротивления. Его проекция Fx — ex, Rx — Pi — Pz — 3, соответственно. C Pi и Pz положительны constants. At начальная точка, точка находилась в крайнем положении, определяемом координатой x od, и была выпущена без начальной скорости. Найти уравнение движения точки с помощью метода ван дер поля. Решение. Дифференциальное уравнение движения точки mX Fx Rx.

Затем определяется искомый момент инерции однородной плоской фигуры путем суммирования моментов инерции всех элементарных площадей. Людмила Фирмаль

Для конкретных значений Fx и Rx ТХ — СХ-видеорегистратор PTX-Pax3, или Х х — р а-P3X3, 1 Ниже эта задача решается эквивалентным методом линеаризации задача 20.5 с сравнительной оценкой различных решений. Вот, кг с m, 2ni fiilm, n 3, m, 1 И л положительны. Мы ищем решение Формулы 1 x и ее первой производной, A, в виде х а 0 грех а 4- х 0,а аа 0 потому что а 2 Где a и a — переменная амплитуда и начальные фазы, которые подлежат последующим решениям. Если сравнить уравнения 1 и 4, приведенные в обзоре теории, то можно сказать, что p, f x, j — la 3 найдено. asinij , Л AA cosip, пиши с sinф, Ак cosф −2лхаАcosф-Лза А8 cosф.

Предварительно вычислите определенный интеграл, чтобы найти и t 2р 2л J p az1pf, и a cos f cos f b f, c a81pf, ak cosf sin f t f, учитывая уравнение 3, в предположении, что A-постоянная 5 часов вечера b81pf, fl A COS f COS f b f — 2л А. Дж коза ф т ф-Lzd А3 Дж Коза Ф УГ, 4 с a81pf, Ак со Ф грех ф т ф −2 ща Дж cosфsinфсГф-л8а3А3 cos3фsinфф ф.

Формула, используемая при вычислении интеграла 4 потому что ф у Я cos2ф, cos1ф А cos2ф 1 cos4ф И если вы присваиваете SOF x интегралу 5 2р Джей с ф грех, Ак cosф cosф ф −2пп Ак-Джей nn3a3A 6 Путем введения интегралов 7 и 8 в укороченное уравнение ван дер поля 6 и 7, приведенное в обзоре теории Формула 8 Если вы разделите переменные, вы найдете r mt С другой стороны Мы пишем 8 9 У Если мы интегрируем это уравнение Иначе говоря В-в 1 л ы Ки — П Здесь Интеграл константы CI является предметом для последующих решений. решение уравнения 11 на a Интеграл уравнения 9 равен 13 Введем результаты 12 и 13 в уравнение 2. х грех м Джи — Е-Р 1. потому что Т КТ С. В.

Если подставить начальные условия i 0, x-a0 в уравнение 14 и присвоить начальные условия t 0 и jf 0 уравнению 15, то получим уравнение. После решения этой системы C4a 2, Cj V14-X2a a0..Узнайте больше. Используйте эти значения Cx и Cj для описания желаемой подгонки в следующей форме КЛ х 1аи-Ся Ле-2njl Потому что КТ.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Метод медленно меняющихся амплитудСкачать

ВАН ДЕР ПОЛЯ УРАВНЕНИЕ

ВАН ДЕР ПОЛЯ УРАВНЕНИЕ — нелинейное обыкновенное дифференциальное уравнение 2-го порядка

Является важным частным случаем Льенара уравнения. В. д. П. у. описывает свободные автоколебания одной из простейших нелинейных колебательных систем (осциллятора Ван дер Поля). В частности, уравнение (1) служит математич. моделью (при ряде упрощающих предположений) лампового генератора на триоде в случае кубич. характеристики лампы. Характер решений уравнения (1) был впервые подробно изучен Б. Ван дер Полем (см. [1]).

Уравнение (1) эквивалентно системе двух уравнений относительно фазовых переменных х, v:

Иногда вместо х удобнее ввести переменную z (t) = ∫ t ₀ х (τ) dτ; тогда уравнение (1) приведется к уравнению

являющемуся частным случаем Рэлея уравнения. Если вместе с переменной х рассмотреть переменную 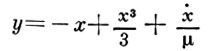, ввести новое время τ = i/μ и положить

ε = μ 2 , то вместо уравнения (1) получим систему

При любом μ > 0 в фазовой плоскости системы (2) существует единственный устойчивый предельный цикл, к к-рому при t → ∞ приближаются все остальные траектории (кроме положения равновесия в начале координат); этот предельный цикл адекватен автоколебаниям осциллятора Ван дер Поля (см. [2]-[4]).

При малых μ автоколебания осциллятора (1) близки к простым гармоническим колебаниям (см. Нелинейные колебания) с периодом 2π и с определенной амплитудой. Для вычисления колебательного процесса с большей точностью применяются асимптотич. методы. При возрастании μ автоколебания осциллятора (1) все более отклоняются от гармонич. колебаний. При больших μ уравнение (1) описывает релаксационные колебания с периодом (в первом приближении) 1,614 μ. Известны более точные асимптотич. разложения величин, характеризующих релаксационные колебания (см. [5]); изучение этих колебаний равносильно исследованию решений системы (3) с малым параметром ε при производной (см. [6]).

описывает поведение осциллятора Ван дер Поля под воздействием внешнего периодич. возмущения. Здесь наиболее важны изучение явления захватывания частоты (существования периодич. колебаний) и исследование биений (возможности почти периодич. колебаний; см. [2], [4]).

Лит.: [1] Van der Рol В., «Phil. Mag.», 1922, ser. 6, v. 43, p. 700-19; 1926, ser. 7, v. 2, p. 978-92; [2] Андронов А. А., Витт A. A., Xайкин С. Э., Теория колебаний, 2 изд., М., 1959; [3] Лефшец C., Геометрическая теория дифференциальных уравнений, пер. с англ., М., 1961; [4] Стокер Дж., Нелинейные колебания в механических и электрических системах, пер. с англ., 2 изд., М., 1953; [5] Дородницын А. А., «Прикл. матем. и механика», 1947, т. 11, с. 313-28; [6] Мищенко Е. Ф., Розов Н. X., Дифференциальные уравнения с малым параметром и релаксационные колебания, М., 1975.

1. Математическая Энциклопедия. Т. 1 (А — Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] — М., «Советская Энциклопедия», 1977, 1152 стб. с илл.

Видео:Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Метод Ван-дер-Поля

Видео:Андреенко А. С. - Общая физика для геологов - Уравнение Ван-дер-ВаальсаСкачать

Содержание

Видео:Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

Цель курсового проекта [ править ]

Задачей данной работы является сравнение прямого решения и метода Ван-дер-Поля приближённого решения уравнения.

Видео:Урок 195. Изотермы реального газаСкачать

Описание метода [ править ]

В своих исследованиях Ван-дер-Поль рассматривал уравнения с малым положительным параметром ε

Оно описывает колебательные движения в среде низкого трения.Уравнение (1) называют квазилинейным, а колебания соответственно квазилинейными. Функция f может быть весьма различной, но мы будем рассматривать в виде (1а).

называется порождающим и описывает обычные гармонические колебания. Общее решение записывается в виде:

Ван-дер-Поль предложил, что приближённое решение уравнения (1) можно представить так же как и решение уравнения (2), только с изменяющимися амплитудой а и фазой φ, этот метод был назван методом «Медленно меняющихся коэффициентов». Которые находятся из системы дифференциальных уравнений с разделяющимися переменными.

Уравнения (3), так называемые «укороченные уравнения» Ван-дер-Поля, позволяют сравнительно просто получить приближенное решение исходного уравнения (1). Перейдем к составлению «укороченных уравнений» для рассматриваемого уравнения (1), или эквивалентной ему системы двух уравнений первого порядка

Прежде всего, заметим, что при ε=0 уравнение (1) превращается в дифференциальное уравнение обычного гармонического осциллятора, и тогда решение системы (4) имеет вид:

где а и φ— постоянные интегрирования.

Будем отыскивать решение уравнения (4) при достаточно малых значениях параметра ε в виде выражений (5), но уже считая а и φ не постоянными, а некоторыми функциями времени. Для этого будем рассматривать выражения (5) не как решения уравнения (4) при ε = 0, а как формулы замены старых переменных х и у на новые переменные а и φ.

Продифференцировав выражения (5) по t, подставим значения производных в уравнениях (4).

Разрешая систему (6) относительно da/dt и Ψ , находим систему уравнений:

Система дифференциальных уравнений (7) эквивалентна рассматриваемой исходной системе (4). Из системы (7) видно, что медленные и быстрые движения для Ψ разделены. Усредняя правые части системы (7) мы получим:

Где A(a) и B(a) имеют вид:

Уравнения (8) будем называть укороченными уравнениями или уравнениями Ван-дер-Поля. Они значительно проще исходной системы (7), поскольку первое уравнения может быть проинтегрировано независимо от второго. В системе (8) медленные и быстрые движения для разделены. Интегрируя первое из уравнений этой системы, мы находим закон изменения амплитуды. Очень часто в прикладных задачах бывает достаточно найти только зависимость амплитуды от времени.

Итак, метод Ван-дер-Поля решения уравнения (1) состоит в переходе от переменной х и y к переменным а и (которые мы будем называть переменными Ван-дер-Поля) и к замене точных уравнений (7) укороченной системой (8).

В заключении стоит заметить, что метод Ван-дер-Поля хорошо работает только при малых параметрах ε

Видео:Уравнение Ван-дер-Ваальса и опыт Джоуля и ТомсонаСкачать

Фазовые портреты [ править ]

С помощью пакета Matlab были построены фазовые портреты для метода Ван-дер-Поля и приближенного численного метода решения при различных параметрах ε.

📽️ Видео

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Решение уравнения ЛагранжаСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Уравнение Ван дер Ваальса. Часть 1. Межмолекулярные взаимодействия. Изотермы Ван дер Ваальса.Скачать

Закон БернуллиСкачать

Scilab 2. ODEСкачать

Теплофизика Л8. Реальные газы. Уравнение Ван дер Ваальса для приведенных величинСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать