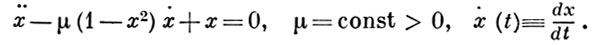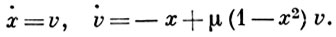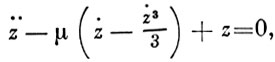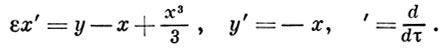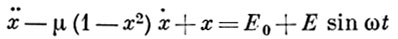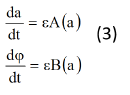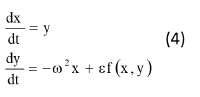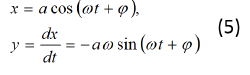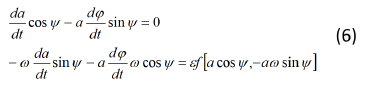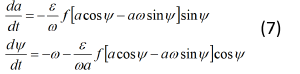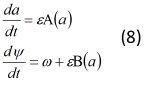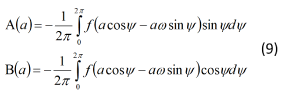Уравнение ван дер поля график (6 видео)

Содержание

Уравнение ван дер Поля
Феномен уравнения Ван Дер Поля
Дискретный осциллятор ван дер Поля: конечные разности и медленные амплитуды
ВАН ДЕР ПОЛЯ УРАВНЕНИЕ
Метод Ван-дер-Поля
Содержание
Цель курсового проекта [ править ]
Описание метода [ править ]
Фазовые портреты [ править ]
🔥 Видео

Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Уравнение ван дер Поля

Видео:Уравнение Ван дер ВаальсаСкачать

Феномен уравнения Ван Дер Поля

Настоящий обзор посвящен знаменитому голландскому ученому Балтазару ван дер Полю, который внес ощутимый вклад в развитие радиотехники, физики и математики. В обзоре выделен лишь один момент его творчества, связанный с уравнением, носящим его имя, и удивительно широким диапазоном применения этого уравнения в естествознании. В обзоре изложены следующие вопросы.
Биография ван дер Поля, его уравнение и предполагаемые предшественники.
О вкладе А.А. Андронова в теорию автоколебаний.

Подробнее о Феномен уравнения Ван Дер Поля
1682 просмотра

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Дискретный осциллятор ван дер Поля: конечные разности и медленные амплитуды

Для дискретизации времени в дифференциальном уравнении движения осциллятора (генератора) ван дер Поля предложено использовать сочетание численного метода конечных разностей и асимптотического метода медленно меняющихся амплитуд. Разностные аппроксимации временных производных выбираются таким образом, чтобы, во-первых, сохранить в дискретном времени консервативность и собственную частоту линейного контура автоколебательной системы.

Видео:Уравнение Ван дер Ваальса. Часть 1. Межмолекулярные взаимодействия. Изотермы Ван дер Ваальса.Скачать

ВАН ДЕР ПОЛЯ УРАВНЕНИЕ

ВАН ДЕР ПОЛЯ УРАВНЕНИЕ — нелинейное обыкновенное дифференциальное уравнение 2-го порядка

Является важным частным случаем Льенара уравнения. В. д. П. у. описывает свободные автоколебания одной из простейших нелинейных колебательных систем (осциллятора Ван дер Поля). В частности, уравнение (1) служит математич. моделью (при ряде упрощающих предположений) лампового генератора на триоде в случае кубич. характеристики лампы. Характер решений уравнения (1) был впервые подробно изучен Б. Ван дер Полем (см. [1]).

Уравнение (1) эквивалентно системе двух уравнений относительно фазовых переменных х, v:

Иногда вместо х удобнее ввести переменную z (t) = ∫ t ₀ х (τ) dτ; тогда уравнение (1) приведется к уравнению

являющемуся частным случаем Рэлея уравнения. Если вместе с переменной х рассмотреть переменную 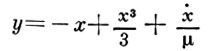, ввести новое время τ = i/μ и положить

ε = μ 2 , то вместо уравнения (1) получим систему

При любом μ > 0 в фазовой плоскости системы (2) существует единственный устойчивый предельный цикл, к к-рому при t → ∞ приближаются все остальные траектории (кроме положения равновесия в начале координат); этот предельный цикл адекватен автоколебаниям осциллятора Ван дер Поля (см. [2]-[4]).

При малых μ автоколебания осциллятора (1) близки к простым гармоническим колебаниям (см. Нелинейные колебания) с периодом 2π и с определенной амплитудой. Для вычисления колебательного процесса с большей точностью применяются асимптотич. методы. При возрастании μ автоколебания осциллятора (1) все более отклоняются от гармонич. колебаний. При больших μ уравнение (1) описывает релаксационные колебания с периодом (в первом приближении) 1,614 μ. Известны более точные асимптотич. разложения величин, характеризующих релаксационные колебания (см. [5]); изучение этих колебаний равносильно исследованию решений системы (3) с малым параметром ε при производной (см. [6]).

описывает поведение осциллятора Ван дер Поля под воздействием внешнего периодич. возмущения. Здесь наиболее важны изучение явления захватывания частоты (существования периодич. колебаний) и исследование биений (возможности почти периодич. колебаний; см. [2], [4]).

Лит.: [1] Van der Рol В., «Phil. Mag.», 1922, ser. 6, v. 43, p. 700-19; 1926, ser. 7, v. 2, p. 978-92; [2] Андронов А. А., Витт A. A., Xайкин С. Э., Теория колебаний, 2 изд., М., 1959; [3] Лефшец C., Геометрическая теория дифференциальных уравнений, пер. с англ., М., 1961; [4] Стокер Дж., Нелинейные колебания в механических и электрических системах, пер. с англ., 2 изд., М., 1953; [5] Дородницын А. А., «Прикл. матем. и механика», 1947, т. 11, с. 313-28; [6] Мищенко Е. Ф., Розов Н. X., Дифференциальные уравнения с малым параметром и релаксационные колебания, М., 1975.

Математическая Энциклопедия. Т. 1 (А — Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] — М., «Советская Энциклопедия», 1977, 1152 стб. с илл.

Видео:Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Метод Ван-дер-Поля

Видео:Уравнение Ван дер Ваальса. Часть 2. Критические параметры. Критическое состояние.Скачать

Содержание

Видео:Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Цель курсового проекта [ править ]

Задачей данной работы является сравнение прямого решения и метода Ван-дер-Поля приближённого решения уравнения.

Видео:Основы теплотехники. Реальные газы. Уравнение Ван дер Ваальса. Решение задач.Скачать

Описание метода [ править ]

В своих исследованиях Ван-дер-Поль рассматривал уравнения с малым положительным параметром ε

Оно описывает колебательные движения в среде низкого трения.Уравнение (1) называют квазилинейным, а колебания соответственно квазилинейными. Функция f может быть весьма различной, но мы будем рассматривать в виде (1а).

называется порождающим и описывает обычные гармонические колебания. Общее решение записывается в виде:

Ван-дер-Поль предложил, что приближённое решение уравнения (1) можно представить так же как и решение уравнения (2), только с изменяющимися амплитудой а и фазой φ, этот метод был назван методом «Медленно меняющихся коэффициентов». Которые находятся из системы дифференциальных уравнений с разделяющимися переменными.

Уравнения (3), так называемые «укороченные уравнения» Ван-дер-Поля, позволяют сравнительно просто получить приближенное решение исходного уравнения (1). Перейдем к составлению «укороченных уравнений» для рассматриваемого уравнения (1), или эквивалентной ему системы двух уравнений первого порядка

Прежде всего, заметим, что при ε=0 уравнение (1) превращается в дифференциальное уравнение обычного гармонического осциллятора, и тогда решение системы (4) имеет вид:

где а и φ— постоянные интегрирования.

Будем отыскивать решение уравнения (4) при достаточно малых значениях параметра ε в виде выражений (5), но уже считая а и φ не постоянными, а некоторыми функциями времени. Для этого будем рассматривать выражения (5) не как решения уравнения (4) при ε = 0, а как формулы замены старых переменных х и у на новые переменные а и φ.

Продифференцировав выражения (5) по t, подставим значения производных в уравнениях (4).

Разрешая систему (6) относительно da/dt и Ψ , находим систему уравнений:

Система дифференциальных уравнений (7) эквивалентна рассматриваемой исходной системе (4). Из системы (7) видно, что медленные и быстрые движения для Ψ разделены. Усредняя правые части системы (7) мы получим:

Где A(a) и B(a) имеют вид:

Уравнения (8) будем называть укороченными уравнениями или уравнениями Ван-дер-Поля. Они значительно проще исходной системы (7), поскольку первое уравнения может быть проинтегрировано независимо от второго. В системе (8) медленные и быстрые движения для разделены. Интегрируя первое из уравнений этой системы, мы находим закон изменения амплитуды. Очень часто в прикладных задачах бывает достаточно найти только зависимость амплитуды от времени.

Итак, метод Ван-дер-Поля решения уравнения (1) состоит в переходе от переменной х и y к переменным а и (которые мы будем называть переменными Ван-дер-Поля) и к замене точных уравнений (7) укороченной системой (8).

В заключении стоит заметить, что метод Ван-дер-Поля хорошо работает только при малых параметрах ε

Видео:7 класс, 35 урок, Графическое решение уравненийСкачать